文巾解题 46. 全排列

Posted 2021-09-06 UQI-LIUWJ

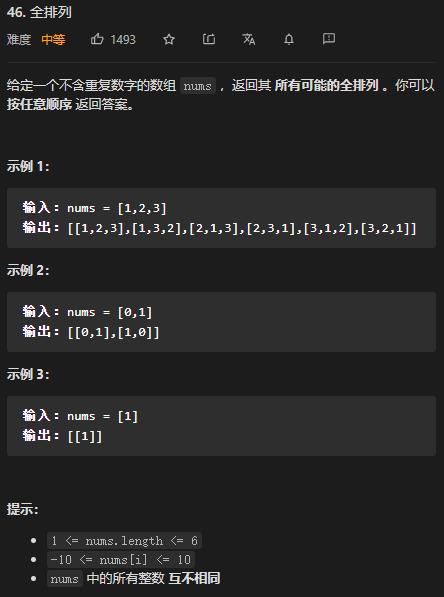
1 题目描述

2 解题思路 ：回溯

• 如果解决一个问题有多个步骤，每一个步骤有多种方法，题目又要我们找出所有的方法，可以使用回溯算法；
• 回溯算法是在一棵树上的 深度优先遍历（因为要找所有的解，所以需要遍历）；
• 组合问题，相对于排列问题而言，不计较一个组合内元素的顺序性（即 [1, 2, 3] 与 [1, 3, 2] 认为是同一个组合），因此很多时候需要按某种顺序展开搜索，这样才能做到不重不漏。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        ret=[]
        def dfs(lst,tmp):
            if(len(tmp)==1):
                ret.append(lst+tmp)
                return
            
            for i in tmp:
                tmp1=tmp.copy()
                tmp1.remove(i)
                lst1=lst.copy()
                dfs(lst+[i],tmp1)

        dfs([],nums)
        return(ret)

这里dfs(lst,tmp)的意思是，nums-tmp的部分已经排列成了lst，我们接下来需要排列tmp中的元素，来构造一种nums中元素的排列方法

我们在tmp中随机选择一个元素，他就是我们lst中的下一个元素。

当tmp只有一个元素的时候，毫无疑问它只有一种排列方法了，此时一种全排列结果就出来了，放入ret数组中。