[人工智能-数学基础-1]:深度学习中的数学地图:计算机数学数值计算数值分析数值计算微分积分概率统计.....
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[人工智能-数学基础-1]:深度学习中的数学地图:计算机数学数值计算数值分析数值计算微分积分概率统计.....相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119710145
目录
1. 为什么要谈这个话题?
深度学习本质上是计算机与数学相融合一门技术。
深度学习的算法,本质上就是数学。深度学习本质上就是通过数学建模,任何通过计算机的手段实现深度学习数学模型的过程,因此,有必要了解深度学习与计算机、与数学的关系。
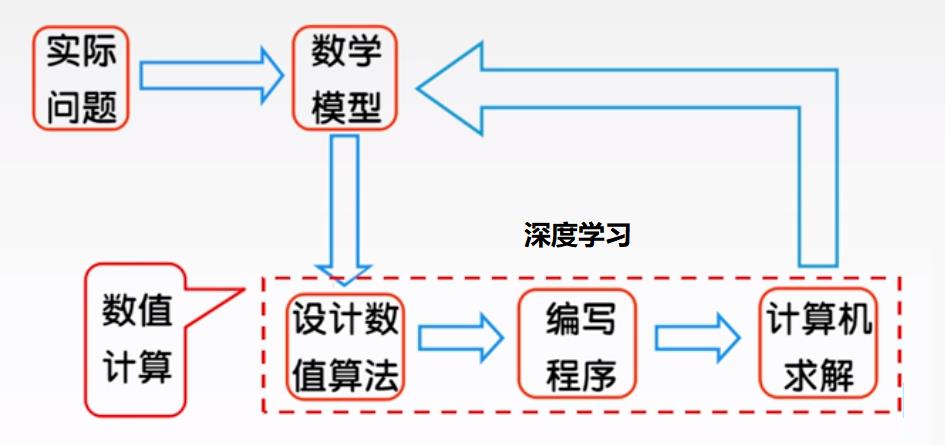
数学建模的过程:就是一个数学领域的问题。
数值计算的过程:这是一个计算机领域+数学领域的问题。
Python编程语言:这是一个计算机领域的问题。
大多数程序员喜欢直接上来就是看代码,然后自己从代码的角度摸索背后的原理,这确实是一种快捷的方法。在互联网领域,这可能是可行的,然而在人工智能深度学习领域,这很难走远、深入。
如果一上来,就能够有一幅地图,这幅地图,能够帮助我们中后期在遇到难题,遇到不懂的问题的时候,能够知道到哪里寻找答案,本文讨论的问题,就是这张地图。
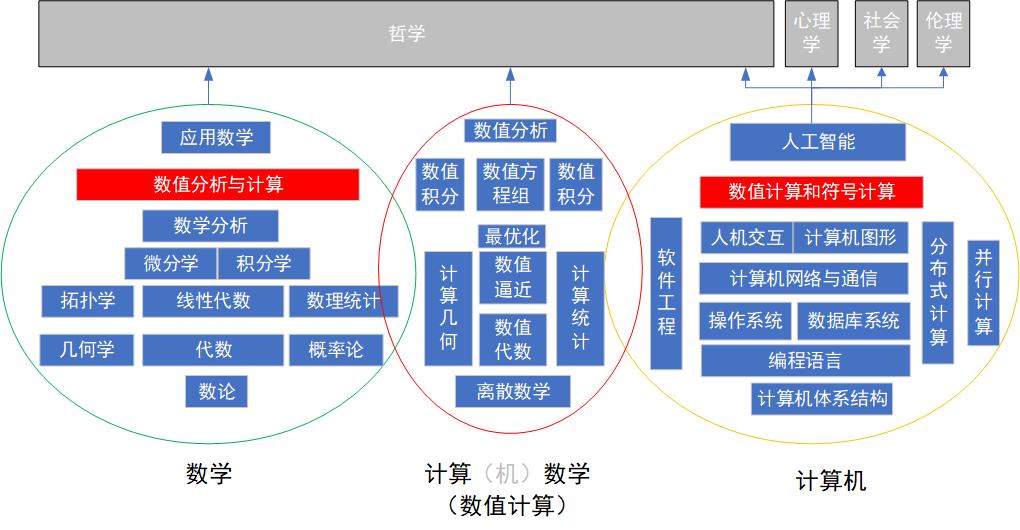

第2章 数学
2.1 概述定义
数学是研究数量、结构、变化、空间以及信息等概念的一门学科。
数学是人类对事物的抽象结构与模式进行严格描述的一种通用手段,可以应用于现实世界的任何问题,所有的数学对象本质上都是人为定义的。
从这个意义上,数学属于形式科学,而不是自然科学。不同的数学家和哲学家对数学的确切范围和定义有一系列的看法。
在人类历史发展和社会生活中,数学发挥着不可替代的作用,同时也是学习和研究现代科学技术必不可少的基本工具。
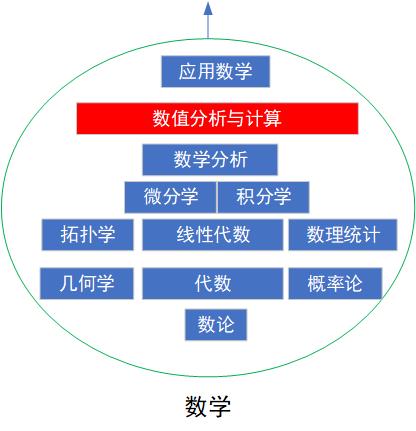
2.2 数学分支

- 数论(number theory ),早期称为算术。数学理论,是纯粹数学的分支之一,主要研究整数的性质,分为初等与高等数论。--- 张量的算术运算。
- 几何学:是研究用数字的方式表达空间结构及性质的一门学科。它是数学中最基本的研究内容之一,与分析、代数等等具有同样重要的地位,并且关系极为密切。--- 数据的可视化。
- 拓扑学(topology),是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。在拓扑学里,重要的拓扑性质包括连通性与紧致性。--- 知识图谱可以认为是一种知识的拓扑结构。
- 代数:是研究确定性现象数量规律的数学分支,是研究数、数量、关系、结构与代数方程的数学分支。代数的研究对象不仅是数字,而是各种抽象化的结构,即关系。例如整数集作为一个带有加法、乘法和序关系的集合就是一个代数结构。其中我们只关心各种关系及其性质,包括线性与非线性关系,变量和函数运算就是属于代数。--- 变量、神经网络参数、普通函数、loss函数、神经网络函数。
- *线性代数:线性(linear)指量与量之间按比例、成直线的关系,它的研究对象是向量,向量空间(或称线性空间),线性变换和有限维的线性方程组。关注的多维空间到多维空间的线性变换关系,通过线性代数,可以把一个复杂的非线性关系转化成多维数据的线性关系。--- 张量的各种矩阵运算、神经网络的正向传播。
- 概率论:是研究随机现象数量规律的数学分支。随机现象是相对于决定性现象而言的,在一定条件下必然发生某一结果的现象称为决定性现象。是一门研究不确定性事情发生的可能性的学问。---分类问题就是不确定性问题,是可能性问题,是猜测问题。
- 数理统计学:是统计学分支学科。以概率论为理论基础,对受随机因素影响的不确定性现象进行大量的观测或试验,以有效的方法获取样本、提取信息,进而对随机现象的统计规律(如方差、分布、相关性等)作判断。--- 大量神经网络参数用随机数初始化。
- 微分学:是指研究函数的导数(变化率)与微分及其在函数研究中的应用,微分学的基础是建立在实数、函数、极限、连续性等一组基本概念之上的。研究自变量在无穷小的变化区间内引起因变量变化大小变化的对应关系。--梯度下降就最值、loss函数的最优化、方向传播。
- 积分学:研究积分学的研究对象也是函数,研究是函数坐标轴区间上的面积与自变量的关系,包括定积分与不定积分。微分与积分统称为微积分。---对概率密度函数求积分计算概率大小。
- 数学分析:是专门研究实数与复数及其函数的数学分支。它的发展由微积分开始,并扩展到函数的连续性、可微分及可积分等各种特性。这些特性,有助我们应用在对物理世界的研究,研究及发现自然界的规律。---链式求导
- 数值计算/计算数学:计算数学也叫做数值计算方法或数值分析,指有效使用数字计算机求上述数学问题近似解的方法与过程,以及由相关理论构成的学科。数值计算主要研究如何利用计算机更好的解决各种数学问题,包括连续系统离散化和离散形方程的求解,并考虑误差、收敛性和稳定性等问题。---线性拟合、梯度下降、数值积分、数值微分.......
第3章 计算机科学
3.1 什么是计算机与计算机科学
计算机是一种进行算术和逻辑运算的机器,而且对于由若干台计算机联成的系统而言还有通信问题,并且处理的对象都是信息,因而也可以说,计算机科学是研究信息处理的科学。
计算机科学的大部分研究是基于“冯·诺依曼计算机”和“图灵机”的,它们是绝大多数实际机器的计算模型。
3.2 研究领域
计算机科学学科的4个主要领域:计算理论,算法与数据结构,编程方法与编程语言,以及计算机元素与架构。
研究对象的关键技术领域:软件工程,操作系统,数据库系统,人机交互,计算机图形学,计算机网络与通信,并行计算,分布式计算,机器翻译,数值和符号计算,人工智能。
- 软件工程:软件工程是对于设计、实现和修改软件的研究,以确保软件的高质量、适中的价格、可维护性,以及能够快速构建。它是一个系统的软件设计方法,涉及工程实践到软件的应用
- 计算机体系结构:计算机系统结构,或者数字计算机组织,是一个计算机系统的概念设计和根本运作结构。它主要侧重于CPU的内部执行和内存访问地址。这个领域经常涉及计算机工程和电子工程学科,选择和互连硬件组件以创造满足功能、性能和成本目标的计算机。
- 操作系统:是管理计算机硬件与软件资源的计算机程序。操作系统需要处理如管理与配置内存、决定系统资源供需的优先次序、控制输入设备与输出设备、操作网络与管理文件系统等基本事务。操作系统也提供一个让用户与系统交互的操作界面
- 编程语言与计算机编程:程序员编辑程序让电脑执行的过程就叫编程,计算机编程是软件工程的一个分支,编程语言(programming language)可以简单的理解为一种计算机和人都能识别的语言。一种计算机语言让程序员能够准确地定义计算机所需要使用的数据,并精确地定义在不同情况下所应当采取的行动。
- 数据库系统:计算机是用软件逻辑处理数据,数据库是指长期存储在计算机内的,有组织,可共享的数据的集合。数据库中的数据按一定的数学模型组织、描述和存储,具有较小的冗余,较高的数据独立性和易扩展性,并可为各种用户共享,这些数据库研究的重点。
- 人机交互:是一门研究系统与用户之间的交互关系的学问。系统可以是各种各样的机器,也可以是计算机化的系统和软件。人机交互界面通常是指用户可见的部分。用户通过人机交互界面与系统交流,并进行操作。人机交互,可以是图形、也可以是命令行或菜单。
- 计算机网络与通信:计算机网络系统就是利用通信设备和线路将地理位置不同、功能独立的多个计算机系统互联起来,以功能完善的网络软件实现网络中资源共享和信息传递的系统。通过计算机的互联,实现计算机之间的通信,从而实现计算机系统之间的信息、软件和设备资源的共享以及协同工作等功能,其本质特征在于提供计算机之间的各类资源的高度共享,实现便捷地交流信息和交换思想。
- 并行计算:相对于串行计算来说的,研究通过同时使用多种计算资源解决计算问题的过程,是提高计算机系统计算速度和处理能力的一种有效手段。并行计算系统既可以是专门设计的、含有多个处理器的超级计算机,也可以是以某种方式互连的若干台的独立计算机构成的集群。通过并行计算集群完成数据的处理,再将处理的结果返回给用户。
- 分布式计算:分布式计算是一种计算方法,和集中式计算是相对的。研究如何把一个需要非常巨大的计算能力才能解决的问题分成许多小的部分,然后把这些部分分配给许多计算机进行处理,最后把这些计算结果综合起来得到最终的结果。
- 计算机图形学:研究如何在计算机中表示图形、以及利用计算机进行图形的计算、处理和显示的相关原理与算法。深度学习中的计算机视觉,其基础就是计算机图形学。
- 数值计算和符号计算:使用数字计算机求数学问题近似解的方法与过程,以及由相关理论构成的学科。
- 人工智能:研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域的研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。

第4章 数值计算方法
4.1 什么是数值计算/计算数学
计算数学也叫做数值计算方法或数值分析。
数值计算指有效使用数字计算机求数学问题近似解的方法与过程,以及由相关理论构成的学科。包括连续系统的离散化和离散形系统的求解,并考虑误差、收敛性和稳定性等问题。
数值计算主要研究如何利用计算机更好的解决各种数学问题。
计算机解决数学问题的方法与纯数学的方法解决数学问题是不同的,纯数学的方法主要关注数学公式的发现、推导和利用。而计算机解决数学问题时,更多受限于计算机的二进制数据形态,因此自身的特独特方法,这就涉及到数值计算研究的领域。
人工智能机器学习和深度学习,本质上就是一个数值计算问题。
4.2 研究领域
从数学类型来分,数值运算的研究领域包括:
数值分析、数值逼近、数值微分和数值积分、数值代数、最优化方法、常微分方程数值解法、积分方程数值解法、偏微分方程数值解法、计算几何、计算概率统计等。
随着计算机的广泛应用和发展,许多计算领域的问题,如计算物理、计算力学、计算化学、计算经济学等都可归结为数值计算问题。
下面的这些数学问题,在深度学习都得到了应用:
- 数值分析: 数值分析(numerical analysis),为数学的一个分支,是研究分析用计算机求解数学计算问题的数值计算的方法及其理论的学科。它以数字计算机求解数学问题的理论和方法为研究对象,为计算数学的主体部分。
- 离散数学:是研究离散量的结构及其相互关系的数学学科。离散的含义是指不同的连接在一起的元素,主要是研究基于离散量的结构和相互间的关系,其对象一般是有限个或可数个元素。
- 数值代数:它以矩阵理论和数学分析为基础,主要研究线性与非线形代数方程组、代数特征值问题与最小二乘问题等的高效数值解法及其稳定和收敛性质,计算机实现和计算复杂性理论,以及这些方法与理论对于实际问题的应用。
- 数值逼近*:如何将一复杂、非线性函数关系,用较简单函数(线性或非线性)来找到最佳逼近,并且通过量化可以表征误差的大小。
- 数值微分:根据函数在一些离散点的函数值,推算它在某点的导数或某高阶导数的近似值。通常用差商代替微商,或用一能近似代替该函数的较简单的函数(如多项式、样条函数)的相应导数作为所求导数的近似值
- 数值积分:用数值逼近的方法近似计算给定的定积分值。借助于电子计算设备,数值积分可以快速而有效地计算复杂函数的积分。
- 最优化方法:指在某些约束条件下,决定某些可选择的变量应该取何值,使所选定的目标函数达到最优的问题。即运用最新科技手段和处理方法,使系统达到总体最优,从而为系统提出设计、施工、管理、运行的最优方案
- 常微分方程数值解法、
- 积分方程数值解法、
- 偏微分方程数值解法、
- 计算几何、
- 计算概率统计

作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119710145

以上是关于[人工智能-数学基础-1]:深度学习中的数学地图:计算机数学数值计算数值分析数值计算微分积分概率统计.....的主要内容,如果未能解决你的问题,请参考以下文章