[人工智能-深度学习-5]：人工神经元数学模型激活函数人工神经网络

Posted 2021-09-25 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：[人工智能-深度学习-5]：人工神经元数学模型、激活函数、人工神经网络_文火冰糖（王文兵）的博客-CSDN博客

---

目录

第1章 前序知识准备

第2章 人工神经元的数学模型

2.1 概述

2.2 神经元的基本功能

2.3 人工神经元的数学模型的提出

2.5 人工神经元的本质

2.6 神经元的简化模型（不带激活函数）

2.7 人工神经元的种类与应用场合

第3章 激活函数的种类

3.1 Sigmoid函数

3.2 tanh函数函数

3.3 Relu函数

3.4 ELU (Exponential Linear Units) 函数

3.5 激活函数的本质

第4章 人工神经网络ANN的数学模型

4.1 概述

4.2 单层神经网络

4.4 二层神经网络 

4.5 四层神经网络

4.6 深层神经网络 

---

第1章 前序知识准备

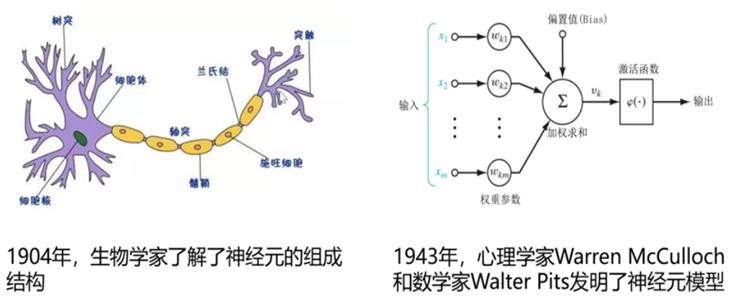
[人工智能-深度学习-4]：生物神经系统与神经元细胞简介

[人工智能-深度学习-4]：生物神经系统与神经元细胞简介_文火冰糖（王文兵）的博客-CSDN博客

第2章 人工神经元的数学模型

2.1 概述

人工神经网络是在现代神经生物学研究基础上提出的模拟生物过程，反映人脑某些特性的一种计算结构。

它不是人脑神经系统的真实描写，而只是它的某种抽象、简化和模拟。

在人工神经网络中，人工记忆神经元常被称为“处理单元”。有时从网络的观点出发常把它称为“节点”。
人工记忆神经元是对生物神经元的一种形式化描述，它对生物神经元的信息处理过程进行抽象，并用数学语言予以描述；对生物神经元的结构和功能进行模拟，并用模型图予以表达。

单个人工神经元具有一定的、简单的学习功能，并能够进行简单的信息处理。

而由神经元构建的神经网络具有大规模的、复杂的学习功能，并能够进行复杂的信息处理。

2.2 神经元的基本功能

神经元和神经网络的两个基本功能：

（1）学习能力 =》 机器学习 =》 深度学习

（2）信息处理能力 =》 后向传播 =》 预测能力，两大基本预测能力包括：

• 回归拟合
• 统计分类

2.3 神经网络的复杂功能包括：

（1）视觉图像处理

（2）听觉音频处理

（3）自然语言处理

（4）语言思维处理

（5）知识图谱

.......

上述的能力基本上都在试图模拟人类大脑的功能，工程上，在某些方面的实际效果甚至已经超过了人类。

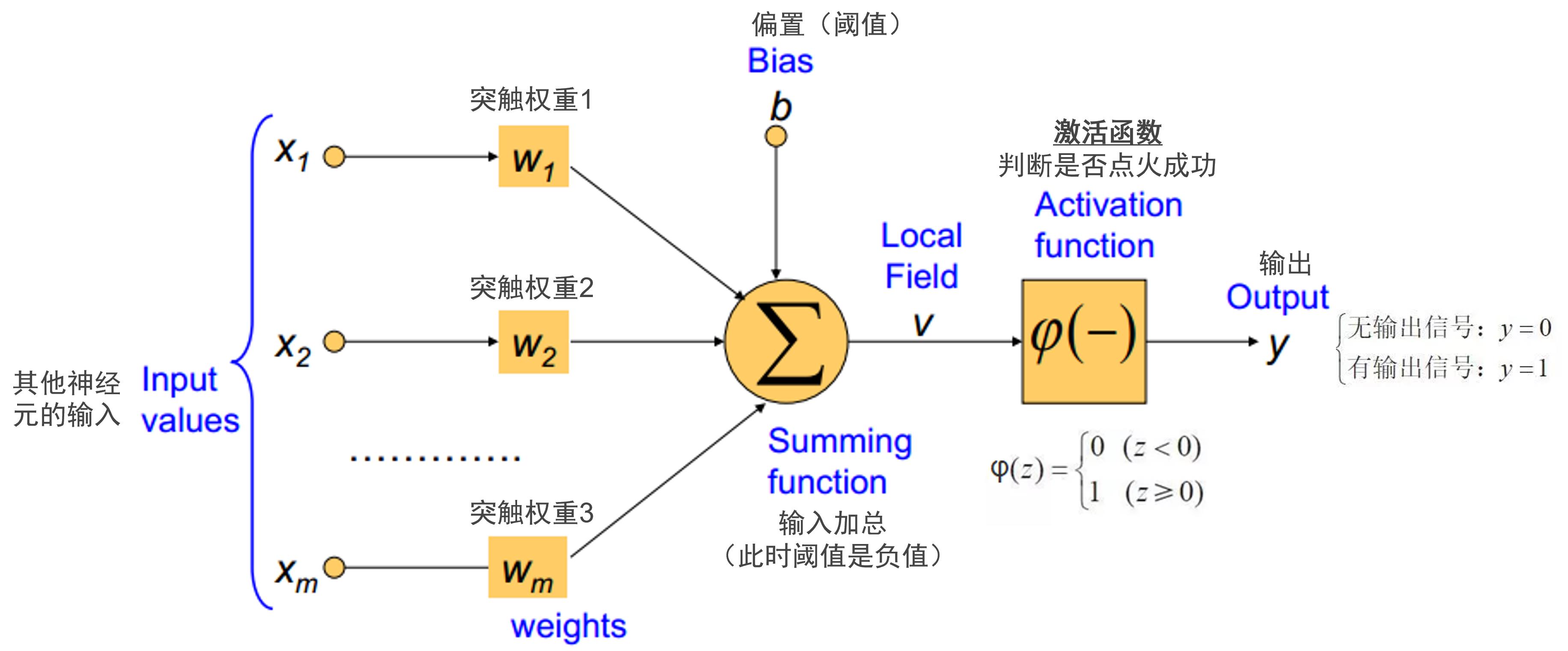
2.3 人工神经元的数学模型的提出

2.4 人工神经元数学模型的数学函数表达式

（1）每一路输入的数学模型

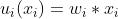
这是一个一元一次线性函数。

该模型模拟的是生物神经元的来自每一路树突的生物电信号的输入。

（2）所有路输入的数学模型：

 

这是一个N元的一次线性函数。

该模型模拟的是生物神经元的细胞体，它把所有输入的生物电信号进行叠加和整合。

（3）带偏置电平的所有输入的数学模型： 

 

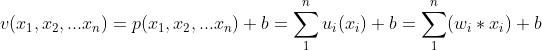
这是一个带偏置b的N元的一次线性函数。

该模型模拟的是生物神经元细胞内部的生物电的电位相对于神经元外部的电位差。

（4）对输出进行抑制的输出模型：激活函数

生物神经元对输入的生物电信号有几个重要的特性，这个特性不是线性函数能模拟的。

• 无论来自树突的输入信号的叠加后的幅度有多大，输出信号的幅度是有限的，不是无限大，也就是说，输出与所有输入之间并非线性的。
• 并非有任何的输入信号，都会导致输出，所有输入信号的幅度，必须得到某个阈值门限，才会有输入信号。

因此，除了对输入信号进行叠加外，还需要一个称为激活函数的函数。其作用如下

• 限制输出

神经元的一次函数，输入与输出是线性关系，因此输出是无穷大。

为了限制神经元的输出信号的幅度，需要通过某种激活函数对输出信号进行限制。

• 提高门槛

神经元的一次函数，输入与输出是线性关系，因此输出是任意值。

生物神经元只有在输入信号得到一定的门限时，才会有输出。

为了模拟生物神经元的门槛功能，需要通过某种激活函数来对输出信号的最低值进行限制。

在深度学习领域，激活函数不是唯一的，有多种不同的激活函数来模拟生物体神经元上述的特性，这里姑且定位：
 

（5）神经元整体的数学模型

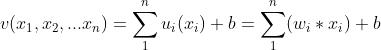
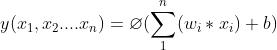
2.5 人工神经元的本质

人工神经元的本质是：N元的1次函数与激活函数构建的复合函数。

2.6 神经元的简化模型（不带激活函数）

（1）一元一次函数

• 只有一个输入参数
• 没有激活函数

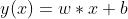
最简单的神经元，就是一个一元一次函数，具有天然的一元一次函数线性拟合的能力。

在之前的文章中，已经多次探讨过一元一次函数的线性拟合问题。

其几何意义就是一根直线。

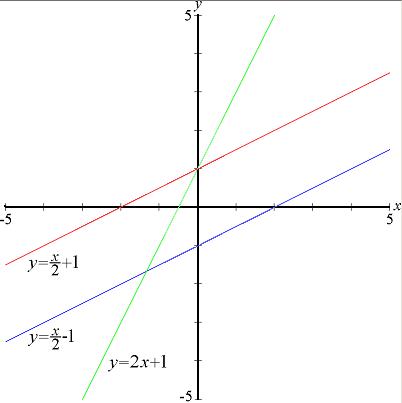
（2）多元一次函数

• 有N一个输入参数
• 没有激活函数

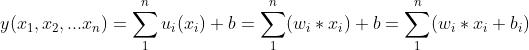
这是一个n个无关的一元一次函数的线性叠加。

其几何意义如下：

2.7 人工神经元输入信号处理的矩阵表达式

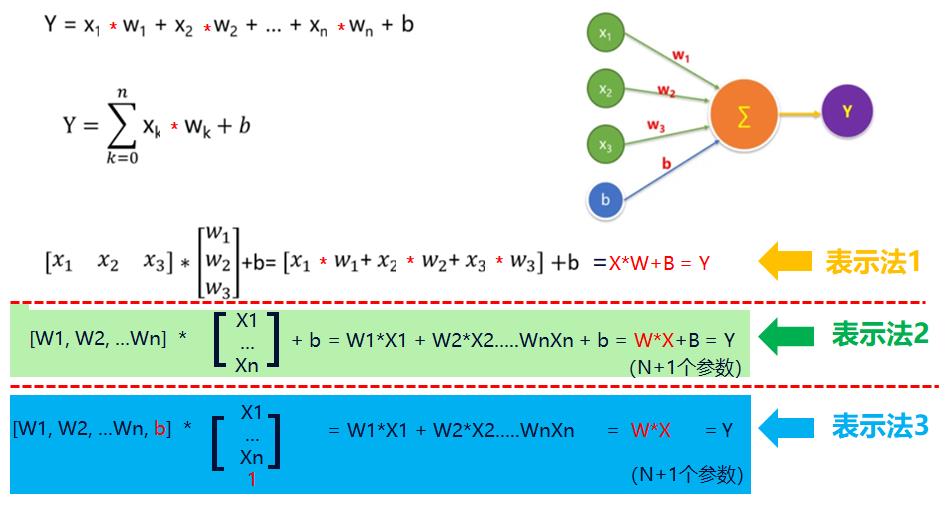
 在上图中，b与w参数进行了整合。

• b对应的输入参数Xi为恒定值
• b与w具有同等的位置。

就得到了最简化的模型 =》 W * X = Y

其中:

• W为n+1长度的行矩阵
• X为n+1长度的列矩阵
• Y为数值标量

2.7 人工神经元的种类与应用场合

第3章 激活函数的种类

参考：[Python系列-16]：人工智能 - 数学基础 -6- 常见数学函数、激活函数大全

[Python系列-16]：人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_文火冰糖（王文兵）的博客-CSDN博客

3.1 Sigmoid函数

（1）公式

（2）图形

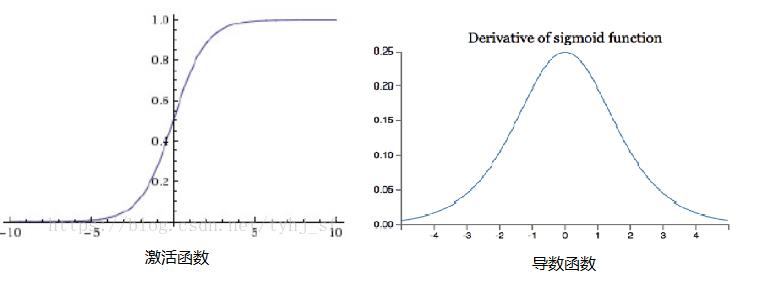
（3）特点

• 无论线性函数的输出是多大，该激活函数把输出限制在(0,1)之间.
• 如果线性函数的输出值为负无穷时，输出为0；
• 如果线性函数的输出值为正无穷时，输出为1.
• 如果线性函数的输出值为0时，输出中值为0.5.
• 导函数平滑

3.2 tanh函数函数

（1）公式

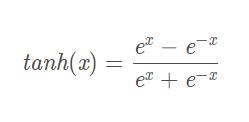
 （2）图形

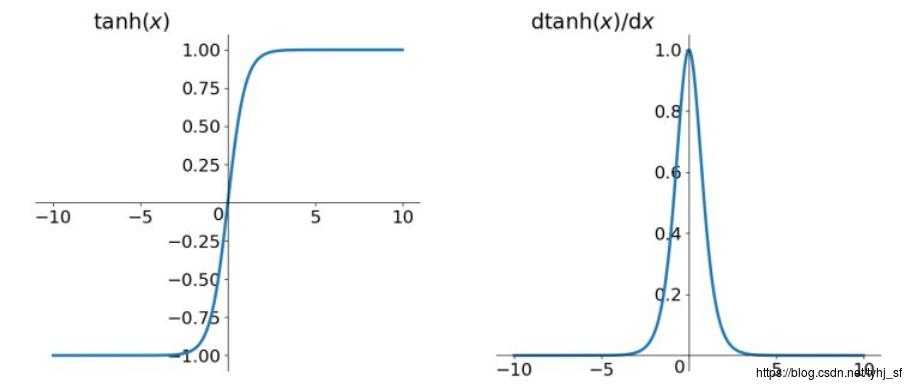
（3）特点

• 无论线性函数的输出是多大，该激活函数把输出限制在(-1,1)之间.
• 如果线性函数的输出值为负无穷时，输出为-1；
• 如果线性函数的输出值为正无穷时，输出为+1.
• 如果线性函数的输出值为0时，输出中值为0.
• 导函数平滑

3.3 Relu函数

（1）公式

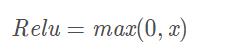
（2）图形

（3）特点

• 无论线性函数的输出是多大，该激活函数把输出限制在(0,+无穷)之间，即把所有的负数都映射成0.
• 如果线性函数的输出值为负数时，输出为0；限制负数幅度映射为0.
• 如果线性函数的输出值为正数时，输出等于输入y = x，不限制正数的映射幅度。
• 如果线性函数的输出值为0时，输出为0.
• 导函数不平滑

3.4 ELU (Exponential Linear Units) 函数

（1）数学公式

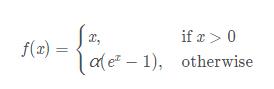
（2）图形表示

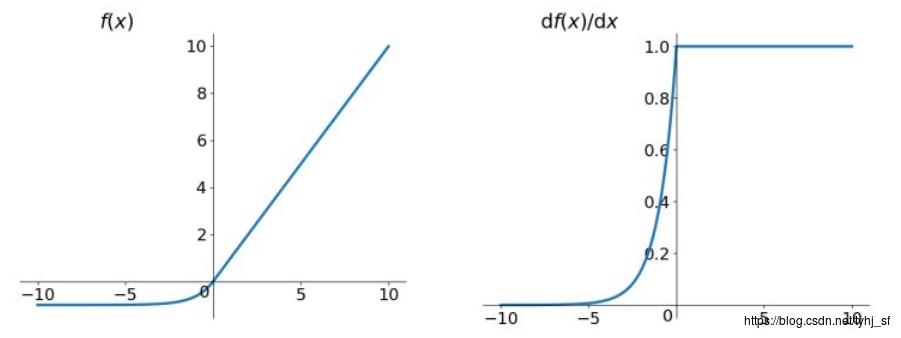
（3）特点

• 当x<0时，采用指数映射，限制负数的幅度。
• 当x>0时，采用线性映射，不限制正数的幅度。
• 当x=0是，映射值为0.
• 导函数不平滑

3.5 激活函数的本质

（1）初等函数

激活函数的本质是初等函数。

（2）空间映射

激活函数的本质，是不同数值空间的映射：

把一个无限幅度的数值空间，映射成一个有限幅度的数值空间。

案例1：指数函数：

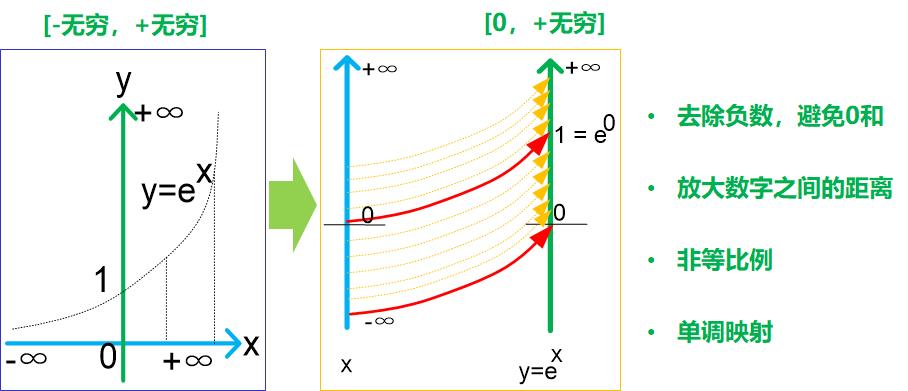
•  自变量x：为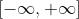的数值空间
•  因变量y：为

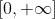
经过映射，原先有的数值的顺序关系还保留，但数字范围被收缩。

案例2： Sigmoid函数：

•  自变量x：为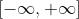的数值空间
•  因变量y：经过映射后，数值被限制在[0, 1]之间.

第4章 人工神经网络ANN的数学模型

4.1 概述

人工神经网络（Artificial Neural Network，即ANN ），是20世纪80 年代以来人工智能领域兴起的研究热点。

它从信息处理角度对人脑神经元网络进行抽象， 建立某种简单模型，按不同的连接方式组成不同的网络。在工程与学术界也常直接简称为神经网络或类神经网络。

神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。

网络的输出则依赖于神经元的网络连接方式，以及各个神经元的权重参数。

而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

最近十多年来，人工神经网络的研究工作不断深入，已经取得了很大的进展，其在模式识别、智能机器人、自动控制、预测估计、生物、医学、经济等领域已成功地解决了许多现代计算机难以解决的实际问题，表现出了良好的智能特性。

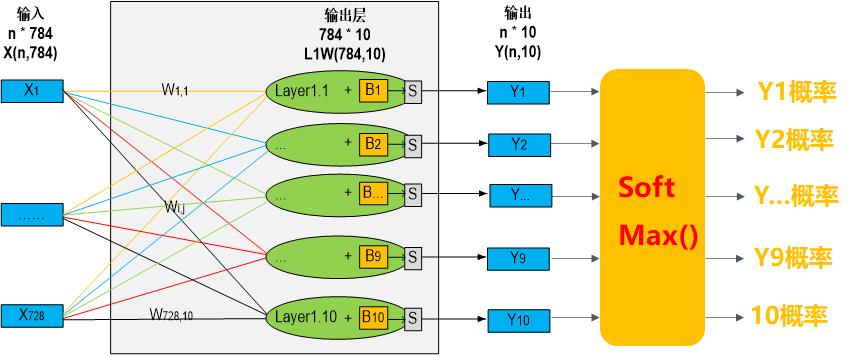
4.2 单层神经网络

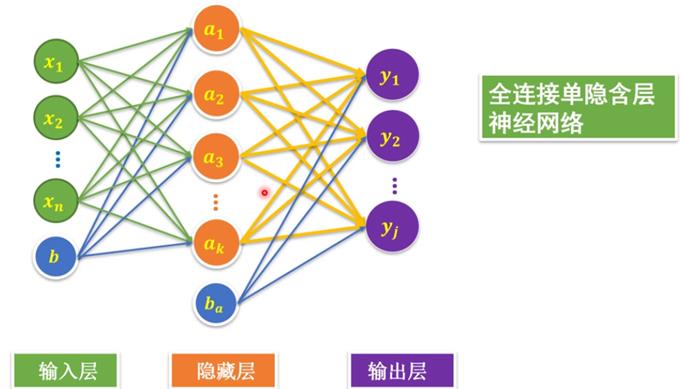
4.4 二层神经网络 

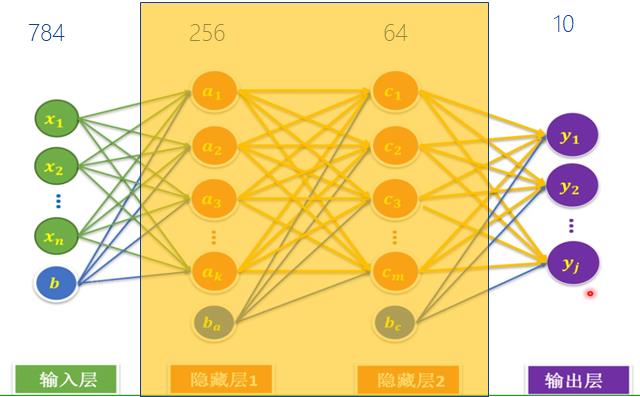
4.5 四层神经网络

4.6 深层神经网络 

深层神经网络的层数可以高达几十层、上百层，甚至上千层。

关于神经网络的连接方式，后续有专门的章节讨论。

---

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：[人工智能-深度学习-5]：人工神经元数学模型、激活函数、人工神经网络_文火冰糖（王文兵）的博客-CSDN博客