Maximum Palindromic String(最大回文串)

Posted 2021-09-05 Dream_it_possible！

Question

        Given a string s,  find the longest  palindromic substring  in s, You may assume that maximum length of s is 1000;

How to determine whether the string is a palindromic?

  /**
     * 判断该字符串是否是回文串
     * Determines whether the string is  a palindromic.
     *
     * @param source
     * @return
     */
    private static boolean check(String source) {
        int i = 0, j = source.length() - 1;
        while (i >= 0 && j > i) {
            if (source.charAt(i) == (source.charAt(j))) {
                i++;
                j--;
            } else {
                return false;
            }
        }
        return true;
    }

        you also can use stack to deteimine whether the string is a palindromic.

Method One

        Find all substring that staisfy the condition, and get one with the largest length .

    /**
     * 方法一:  找出所有满足条件的子串，即回文串，比较长度，取出最长的。
     * method one : Find all substrings that satisfy the condition, and get one with the largest length.
     *
     * @param source
     * @return
     */
    private static String findMaxPalindromicSubStr(String source) {
        String target = "";
        for (int i = 0; i < source.length(); i++) {
            for (int j = i + 1; j < source.length(); j++) {
                String temp = source.substring(i, j+1);
                boolean isPalindromic = check(temp);
                if (isPalindromic) {
                    if (temp.length() > target.length()) {
                        target = temp;
                    }
                }
            }
        }
        return target;
    }

print result:

        We can find have two satisfy string in s, but 'ouphaahpuo' has the maximum length.

        As a result, we can use a dual for loop, but it take a lot of time,It's o(n3). now, Let's find a better method 

Method two

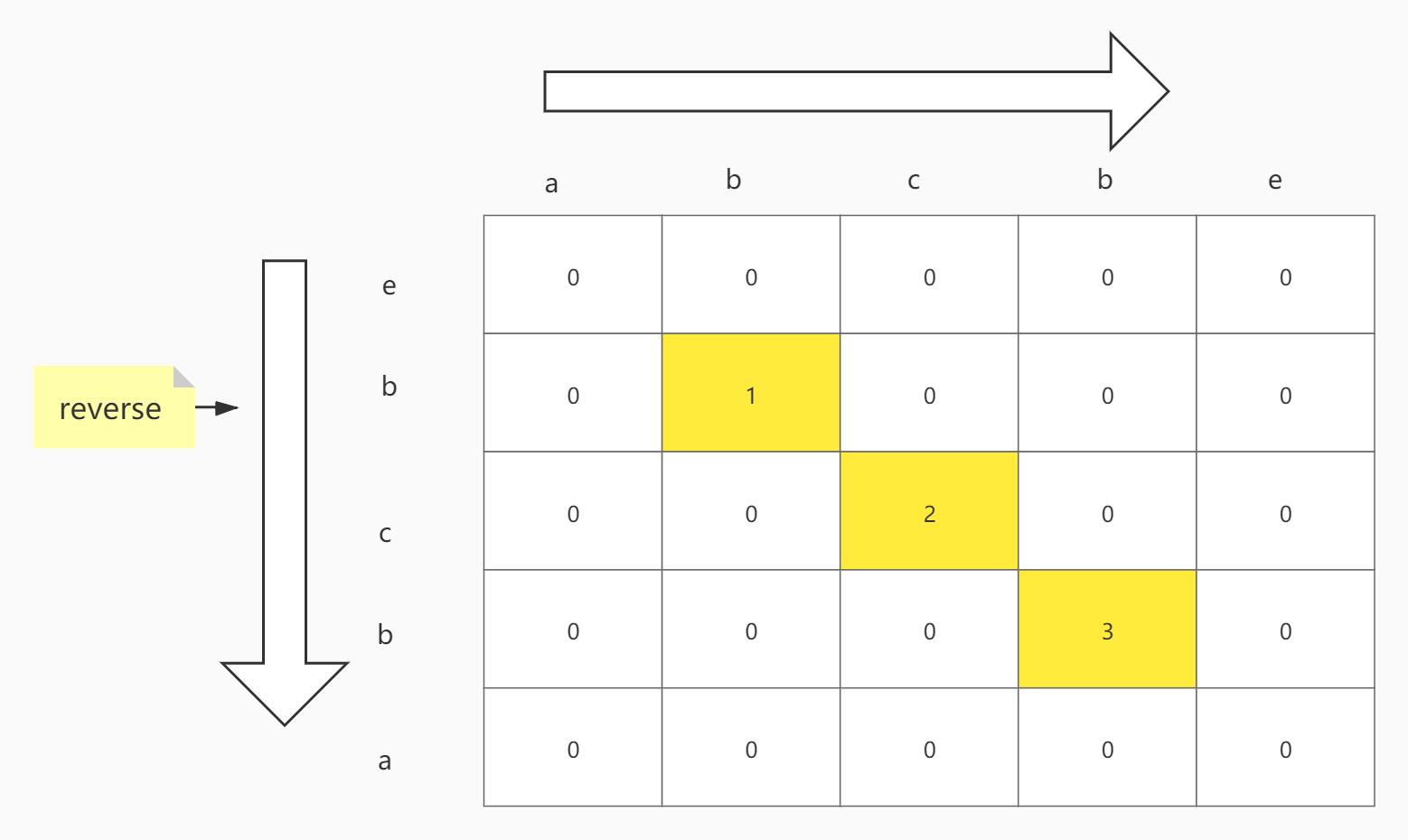
       We can use space for time , Using a two-demensional array,and find equal consecutive equal characters. 

        The last of consecutive value is the maximum palindromic length. The i is the end index of maximum palindromic.

        Please see the flowing chart,  Example string :  abcbe

    /**
     * 方法二: 采用空间换时间的方式，利用二维数组，找到相等的字符并统计连续相等的个数。
     * Method two: use space for time,Using a two-dimensional array, find equal character and count the number of
     * consecutive equal characters.
     */
    private static String findBetterMaxPalindromicSubStr(String source) {
        String reverse = new StringBuilder(source).reverse().toString();
        int length = source.length();
        int maxLen = 0;
        int maxEnd = 0;
        int[][] arr = new int[length][length];
        for (int i = 0; i < length; i++) {
            for (int j = 0; j < length; j++) {
                if (source.charAt(i) == reverse.charAt(j)) {
                    if (i == 0 || j == 0) {
                        arr[i][j] = 1;
                    } else {
                        arr[i][j] = arr[i - 1][j - 1] + 1;
                    }
                    if (arr[i][j] > maxLen) {
                        maxLen = arr[i][j];
                        maxEnd = i;
                    }
                }
            }
        }
        return source.substring(maxEnd - maxLen + 1, maxEnd + 1);
    }

Pring result:

         From what has been discussed above, we can easy find Method Two is superior to Method One. it's o(n2);

Complete Code        

package leetcode100;

/**
 * @author bingbing
 * @date 2021/8/11 0011 11:11
 * 最大回文子串问题
 */
public class MaxPalindromicSubStrProblem {


    public static void main(String[] args) {
        String s = "ajpffpjaaopuouphaahpuo";
        String result = findMaxPalindromicSubStr(s);
        System.out.println(result);
        String r = findBetterMaxPalindromicSubStr(s);
        System.out.println(r);
    }

    /**
     * 方法一:  找出所有满足条件的子串，即回文串，比较长度，取出最长的。
     * method one : Find all substrings that satisfy the condition, and get one with the largest length.
     *
     * @param source
     * @return
     */
    private static String findMaxPalindromicSubStr(String source) {
        String target = "";
        for (int i = 0; i < source.length(); i++) {
            for (int j = i + 1; j < source.length(); j++) {
                String temp = source.substring(i, j + 1);
                boolean isPalindromic = check(temp);
                if (isPalindromic) {
                    if (temp.length() > target.length()) {
                        target = temp;
                    }
                }
            }
        }
        return target;
    }

    /**
     * 方法二: 采用空间换时间的方式，利用二维数组，找到相等的字符并统计连续相等的个数。
     * Method two: use space for time,Using a two-dimensional array, find equal character and count the number of
     * consecutive equal characters.
     */
    private static String findBetterMaxPalindromicSubStr(String source) {
        String reverse = new StringBuilder(source).reverse().toString();
        int length = source.length();
        int maxLen = 0;
        int maxEnd = 0;
        int[][] arr = new int[length][length];
        for (int i = 0; i < length; i++) {
            for (int j = 0; j < length; j++) {
                if (source.charAt(i) == reverse.charAt(j)) {
                    if (i == 0 || j == 0) {
                        arr[i][j] = 1;
                    } else {
                        arr[i][j] = arr[i - 1][j - 1] + 1;
                    }
                    if (arr[i][j] > maxLen) {
                        maxLen = arr[i][j];
                        maxEnd = i;
                    }
                }
            }
        }
        return source.substring(maxEnd - maxLen + 1, maxEnd + 1);
    }


    /**
     * 判断该字符串是否是回文串
     * Determines whether the string is  a palindromic.
     *
     * @param source
     * @return
     */
    private static boolean check(String source) {
        int i = 0, j = source.length() - 1;
        while (i >= 0 && j > i) {
            if (source.charAt(i) == (source.charAt(j))) {
                i++;
                j--;
            } else {
                return false;
            }
        }
        return true;
    }

}