HPU树状数组入门
Posted skywalker767
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了HPU树状数组入门相关的知识,希望对你有一定的参考价值。
树状数组(Binary Indexed Tree)
Author: Skywalker
Creation time:2021/8/10 21:28
Last update:2021/8/12 21:10
情景引入
在处理一段区间的和的时候,我们可以通过前缀和算法来提高运算效率,除去预处理,能做到每次询问 o ( 1 ) o(1) o(1)算出,这个时间复杂度是极其优秀的,但是如果修改一个点后,再次询问一段区间的和,我们发现,最坏情况下,我们要更新 n n n次数组,我们不能接受。那么,如何快速的询问一段区间的长度,并且修改的时候更新速度也要足够优秀,这时候,就体现出了树状数组算法的优越性。
即:能以 o ( l o g n ) o(logn) o(logn)的时间复杂度进行单点修改,以 o ( l o g n ) o(logn) o(logn)的时间复杂度进行区间查询。
l o g log log级别的算法是极其可靠的。 2 31 l o g 2^{31} ~log~ 231 log 后也不过是 31 31 31而已(这边的 l o g log log是以 2 2 2为底)。
前置知识
顾名思义,树状数组是根据树形结构来优化运算,从而达到可观的时间复杂度,我们需要一些工具来进行遍历树的每个节点,来方便我们的运算。
**lowbit函数的定义:**lowbit函数的作用是返回二进制下最后一位 1 1 1代表的十进制数,例如: 12 ( 1100 ) 12(1100) 12(1100),那么他的最后一位 1 1 1所代表的十进制数就是 4 ( 100 ) 4(100) 4(100)。
lowbit函数的实现:
int lowbit(int n)
{
return n & (-n);
}
lowbit函数的证明:
设
x
的
最
低
位
的
1
在
第
k
位
,
那
么
0
~
k
−
1
位
都
是
0
−
x
=
(
∼
x
+
1
)
取
反
加
一
,
取
反
后
0
∼
k
−
1
都
会
变
成
1
,
+
1
后
,
则
0
∼
k
−
1
又
消
成
了
0
第
k
位
变
成
1
,
前
面
都
是
原
来
的
取
反
的
结
果
,
则
为
一
个
零
,
一
个
一
,
取
与
后
为
0
得
证
设x的最低位的1在第k位,那么0~k - 1位都是0\\\\ -x = (\\sim x + 1)取反加一,取反后0 \\sim k -1都会变成1,+1后,则0 \\sim k-1又消成了0\\\\ 第k位变成1,前面都是原来的取反的结果,则为一个零,一个一,取与后为0\\\\ 得证\\\\
设x的最低位的1在第k位,那么0~k−1位都是0−x=(∼x+1)取反加一,取反后0∼k−1都会变成1,+1后,则0∼k−1又消成了0第k位变成1,前面都是原来的取反的结果,则为一个零,一个一,取与后为0得证
lowbit只是一个工具,证明有兴趣可以考虑,无兴趣可看可不看。
树状数组
铺垫了一点点,下面来到我们的树状数组,下面将从:树状数组的理论基础,树状数组的代码实现,树状数组的用途来进行叙述。
树状数组的理论基础:
树状数组 = 前缀和 + 二进制拆分
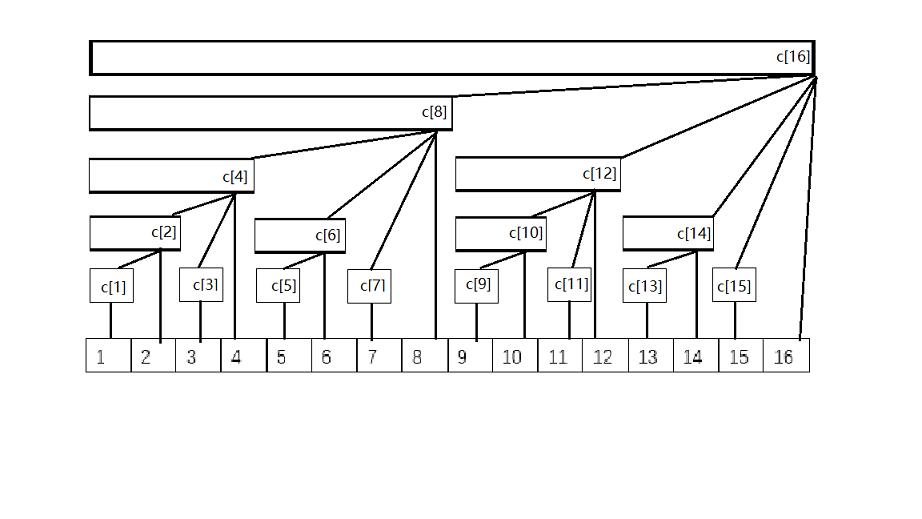
- 每个内部节点 c [ x ] c[x] c[x]保存以它为根的子树的所有节点和。
- 每个内部节点 c [ x ] c[x] c[x]保存的节点个数等于lowbit(x)的位数。
- 除树根外,每个内部节点 c [ x ] c[x] c[x]的父节点是c[x + lowbit(x)]。
- 树的深度为 O ( l o g ( n ) ) O(log(n)) O(log(n))
以上性质来自算法进阶指南.
c [ x ] 保 存 的 是 序 列 a 的 区 间 [ x − l o w b i t + 1 , x ] 的 和 即 : ∑ i = x − l o w b i t ( x ) − 1 x a [ i ] c[x]保存的是序列a的区间[x - lowbit + 1 , x]的和\\\\ 即:\\sum_{i = x - lowbit(x) - 1}^xa[i] c[x]保存的是序列a的区间[x−lowbit+1,x]的和即:i=x−lowbit(x)−1∑xa[i]
树状数组的代码实现:
树状数组支持的基本操作是查询前缀和,即序列第1~x个数的和,[1 , x]已经被划分成了
l
o
g
(
N
)
log(N)
log(N)个小区间,而每个区间,都在
c
c
c数组中,所以查询区间前缀和的代码如下,其时间复杂度为
O
(
l
o
g
N
)
O(logN)
O(logN).
- 查询操作,查询a[1 ~ x]的和
int query(int x)
{
int ans = 0;
for(int i = x;i >= 1;i -= lowbit(i)) ans += c[i];
return ans;
}
当然,如果查询 l ∼ r l \\sim r l∼r的前缀和,我们可以利用前缀和思想, q u e r y ( r ) − q u e r y ( l − 1 ) query(r) - query(l - 1) query(r)−query(l−1)
树状数组支持的第二个操作是单点增加,在 x x x位置加上value后,树状数组只需要 l o g ( N ) log(N) log(N)的时间复杂度,维护树状结构和其性质。
- 单点插入 , 在x位置插入一个值v
void add(int x , int v)
{
for(int i = x;i <= n;i += lowbit(i)) c[i] += v;
}
至此,树状数组的两大基础操作,已经全部概述完毕,下面是树状数组的应用。
树状数组的应用:
- 因为其独特的结构,用于存储,修改,和查询,前缀和能有很好的效果
- 求逆序对
若 i < j i < j i<j,且 a [ i ] > a [ j ] a[i] > a[j] a[i]>a[j],则称 a [ i ] a[i] a[i]与 a [ j ] a[j] a[j]构成逆序对,我们已知的逆序对求法较为优秀的算法是归并排序,然而,树状数组也可以做到。
可以正序求出逆序对,也可以逆序遍历求出逆序对,这边给出的是逆序求逆序对的方法。
- 在序列 a a a的数值范围上建立树状数组,对于每个 a [ i ] a[i] a[i],累加到答案 a n s ans ans中。
- 执行单点增加操作,把位置 a [ i ] a[i] a[i]上出现的数加上1,相当于( t r [ a [ i ] ] + + tr[a[i]] ++ tr[a[i]]++)。
for(int i = n; i ; i --)
{
ans += query(a[i] - 1);
add(a[i] , 1);
}
- ans即为所求
树状数组的拓展应用:
利用差分知识,我们可以维护区间修改,单点查询,篇幅有限,这里不展开了。
练习题目
| 题目名称 | 考察知识点 |
|---|---|
| Sort it(例题1) | 树状数组求逆序对 |
| Inversion | 离散化,树状数组求逆序对 |
| 敌兵布阵(例题2) | 树状数组模版题 |
| Japan | 树状数组求逆序对 |
| Matrix | 二维树状数组 |
| A Simple Problem with Integers | 树状数组+差分+推公式 |
| Stars | 树状数组求逆序对 |
| Mobile phones | 二维树状数组 |
| Bubble Sort | 树状数组,思维 |
| 空间大师 | 树状数组,二分 |
例题1代码:
#include <bits/stdc++.h>
#define lowbit(x) (x & (-x))
using namespace std;
typedef long long LL;
const int N = 1000;
int n;
int a[N + 10];
LL tr[N + 10];
LL query(int x)
{
LL ans = 0;
for(int i = x;i >= 1;i -= lowbit(i)) ans += tr[i];
return ans;
}
void add(int x , int v)
{
for(int i = x;i <= n;i += lowbit(i)) tr[i] += v;
}
int main()
{
while(~scanf("%d" , &n))
{
LL ans = 0;
memset(tr , 0 , sizeof tr);
for(int i = 1;i <= n;i ++) scanf("%d" , &a[i]);
for(int i = n; i ;i --)
{
ans += query(a[i] - 1);
add(a[i] , 1);
}
printf("%lld\\n" , ans);
}
return 0;
}
例题2代码
#include <bits/stdc++.h>
#define lowbit(x) (x & (-x))
using namespace std;
typedef long long LL;
const int N = 50010;
int n , t;
int a[N];
LL tr[N + 10];
LL query(int x)
{
LL ans = 0;
for(int i = x;i >= 1;i -= lowbit(i)) ans += tr[i];
return ans;
}
void add(int x , int v)
{
for(int i = x;i < N;i += lowbit(i)) tr[i] += v;
}
int main()
{
scanf("%d" , &t);
for(int ii = 1;ii <= t;ii ++)
{
memset(tr , 0 , sizeof tr);
scanf("%d" , &n);
for(int i = 1;i <= n;i ++)
{
scanf("%d" , &a[i]);
add(i , a[i]);
}
printf("Case %d:\\n" , ii);
int x , y;
string op;
while(cin >> op)
{
if(op == "End") break;
scanf("%d %d" , 树状数组从入门到弃疗