整型和浮点数据的储存

Posted 2021-09-04 梦乡回雪

文章目录

• 前言
• 一、整型数据的储存
• • 大小端
• 二、浮点型数组的储存
• • 浮点数并不是简单的二进制补码在计算机中存储
  • 1.IEEE标准
  • • S
    • E
    • • E不全是0或者不全是1
      • E全是1
    • M
  • 举例子：

---

前言

提示：这里可以添加本文要记录的大概内容：
例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、整型数据的储存

大小端

我们知道C语言中的几种数据类型以及对应的大小

char	字符数据类型
short	短整型
int	整形
long	长整型
long long	更长的整形
float	单精度浮点数
double	双精度浮点数

• 那么我们声明定义一个变量a，我们知道数据是以二进制补码储存的，那么写出对应的二进制原反补码相等并转化为十六进制
  

• 而这时我们调用内存去观察a的存储形式，会发现顺序有点不太一样
  

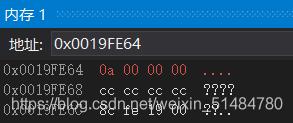
• 原因是因为大小端储存模式

大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址中；
小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地址中。

图解说明小端储存：

那么大端存储就是00 00 00 0a
并且大部分编译器都是小端储存

二、浮点型数组的储存

浮点数并不是简单的二进制补码在计算机中存储

1.IEEE标准

根据国际标准IEEE（电气和电子工程协会） 754，
任意一个二进制浮点数V可以表示成下面的形式：
(-1)^S * M * 2^E

1. (-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。
2. M表示有效数字，大于等于1，小于2。
3. 2^E表示指数位

举例来说： 十进制的5.0，写成二进制是 101.0 ，相当于 1.01×2^2 。 那么，按照上面V的格式，可以得出s=0，
M=1.01，E = 2。

IEEE745规定：对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。

S

也就是说S的一个比特位存放 1或者0表示正负，

E

首先，E为一个无符号整数（unsigned int） 这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的
取值范围为0~2047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，存入内存时E的真
实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。比如，2^10的E
是10，所以保存成32位浮点数时，必须保存成10+127=137，即100010

E不全是0或者不全是1

• E中8个比特位存放时需要先把原来的数字加上127，读取的时候需要减去127 #### E全是0
• 这时，浮点数的指数E等于1-127（或者1-1023）即为真实值， 有效数字M不再加上第一位的1，而是还原为
  0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。

E全是1

• 这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；

M

• 存放有效数据

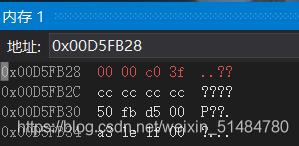
举例子：

查看内存：（也再次验证了小端储存）