LeetCode802. 找到最终的安全状态（图论三色标记法拓扑排序）/847. 访问所有节点的最短路径（特殊的bfs，状态压缩，dp）

Posted 2021-09-01 Zephyr丶J

802. 找到最终的安全状态

2021.8.5 每日一题

题目描述

在有向图中，以某个节点为起始节点，从该点出发，每一步沿着图中的一条有向边行走。如果到达的节点是终点（即它没有连出的有向边），则停止。

对于一个起始节点，如果从该节点出发，无论每一步选择沿哪条有向边行走，最后必然在有限步内到达终点，则将该起始节点称作是 安全 的。

返回一个由图中所有安全的起始节点组成的数组作为答案。答案数组中的元素应当按 升序 排列。

该有向图有 n 个节点，按 0 到 n - 1 编号，其中 n 是 graph 的节点数。图以下述形式给出：graph[i] 是编号 j 节点的一个列表，满足 (i, j) 是图的一条有向边。

示例 1：

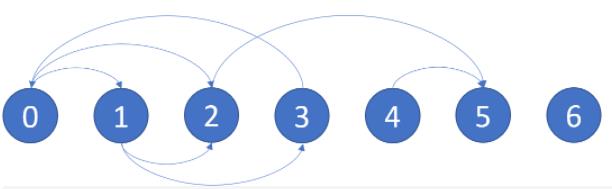
输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]
解释：示意图如上。

示例 2：

输入：graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出：[4]

提示：

n == graph.length
1 <= n <= 104
0 <= graph[i].length <= n
graph[i] 按严格递增顺序排列。
图中可能包含自环。
图中边的数目在范围 [1, 4 * 104] 内。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-eventual-safe-states
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

图论来了

三色标记法，mark一下：

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        //n范围很大，并且边的个数在4*10^4，最多O1了
        //只要是一个圈内的，就不行
        //那么怎么找环呢
        //由一个节点出发，遍历能到达的点，如果最后又能回到自己，就说明找到环了
        //但是该怎么表示呢？？？
        //想了下入度出度怎么搞，但是还是不会

        //学习一下三色标记法的思想，昨天刚看了cms和g1，笑哭
        //三种颜色，0 1 2 白色、灰色、黑色，分别表示没有遍历过，正在遍历或成环、安全节点

        int l = graph.length;
        //节点的颜色
        int[] color = new int[l];
        List<Integer> res = new ArrayList<>();
        //遍历所有节点
        for(int i = 0; i < l; i++){
            //如果不是在环里，就加入结果
            if(threecolor(i, color, graph)){
                res.add(i);
            }
        }
        return res;
    }

    //三色标记法，false表示不安全，即有环
    public boolean threecolor(int idx, int[] color, int[][] graph){
        //如果这个点走过了，那么就直接返回
        //没有这一句会超时
        if(color[idx] > 0)
            return color[idx] == 2;
        //如果到达了一个没有出度的节点，那么说明到头了，这个节点是安全的
        if(graph[idx].length == 0){
            color[idx] = 2;
            return true;
        }
        //先将该节点的颜色标记成灰色
        color[idx] = 1;
        //遍历所有连接的节点
        for(int i = 0; i < graph[idx].length; i++){
            //如果遇到的节点是灰色的，那么说明走到环里了
            if(color[graph[idx][i]] == 1)
                return false;
            //如果有一个节点连接是不安全的，该节点就是不安全的
            if(!threecolor(graph[idx][i], color, graph)){
                return false;
            }
        }
        //如果能走到这里，说明这个点是安全的
        color[idx] = 2;
        return true;
    }
}

拓扑排序（自从那个图论月后就再也没有看到过）：
简单解释：https://www.jianshu.com/p/3347f54a3187

题目扩展：https://blog.csdn.net/qq_41713256/article/details/80805338

在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点。
先统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度减一。
一直做改操作，直到所有的节点都被分离出来。
如果最后不存在入度为0的节点，那就说明有环，不存在拓扑排序，也就是很多题目的无解的情况。

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        //拓扑排序
        //若一个节点出度为0，那么这个节点是安全的
        //如果一个节点所连接的节点，出度都是0，那么该节点也是安全的

        //那么就先找到出度为0的点，然后从这些点的入度遍历，将遍历到点的出度减1，
        //如果出度减到0了，那么说明这个点也是安全的（达到的所有点都是安全的，所以该点是安全的）

        //那么首先找到能到达出度为0节点的点，也可以说是反向建图

        int l = graph.length;
        List<List<Integer>> gra = new ArrayList<>();
        for(int i = 0; i < l; i++){
            gra.add(new ArrayList<>());
        }
        //统计出度的数组，其实没有也可以
        int[] outDeg = new int[l];
        //统计每个点的入度
        for(int i = 0; i < l; i++){
            for(int j = 0; j < graph[i].length; j++){
                gra.get(graph[i][j]).add(i);
            }
            outDeg[i] = graph[i].length;
        }

        //将出度为0的点加入队列
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 0; i < l; i++){
            if(outDeg[i] == 0)
                queue.add(i);
        }

        //然后遍历这些点入度，
        while(!queue.isEmpty()){
            int t = queue.poll();
            //遍历这个点的入度
            List<Integer> temp = gra.get(t);
            for(int i = 0; i < temp.size(); i++){
                //把这些点的出度减1
                int point = temp.get(i);
                outDeg[point]--;
                //如果这个点的出度为0了，那么这个点也要加入队列，方便遍历它连接的点
                if(outDeg[point] == 0)
                    queue.add(point);
            }
        }
        List<Integer> res = new ArrayList<>();
        for(int i = 0; i < l; i++){
            if(outDeg[i] == 0)
                res.add(i);
        }
        return res;
    }
}

847. 访问所有节点的最短路径

2021.8.6 每日一题

题目描述

存在一个由 n 个节点组成的无向连通图，图中的节点按从 0 到 n - 1 编号。

给你一个数组 graph 表示这个图。其中，graph[i] 是一个列表，由所有与节点 i 直接相连的节点组成。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

示例 1：

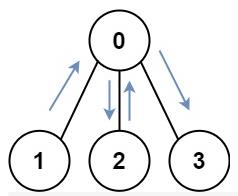
输入：graph = [[1,2,3],[0],[0],[0]]
输出：4
解释：一种可能的路径为 [1,0,2,0,3]

示例 2：

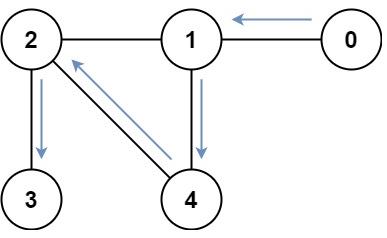
输入：graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出：4
解释：一种可能的路径为 [0,1,4,2,3]

提示：

n == graph.length
1 <= n <= 12
0 <= graph[i].length < n
graph[i] 不包含 i
如果 graph[a] 包含 b ，那么 graph[b] 也包含 a
输入的图总是连通图

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/shortest-path-visiting-all-nodes
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

看了题解，自己写的

第一种：特殊的bfs，状态压缩

这个题主要问题有两个：
一个是不知道从何开始遍历；第二个是遍历过的还能再走
所以做起来有点懵
那么如何解决这两个问题呢？
第一，如果不知道从何遍历，那么就开始把所有点都加入队列，都作为开头
第二，因为这个题是要求所有点都走过才算结束。再看到数据范围不大，12；所以想到用mask存储每个节点遍历的情况，每个位置，1表示这个点经过了， 0表示没有；把节点值 + mask当做组合节点加入队列，就不会有这种遍历过的还能再走这个问题了
另外，再加入一个状态，表示当前走过的路径长度，三元组存入队列

当走到一个位置，mask都为1，那么 说明所有点都走过了。就直接输出
为什么能保证这个输出的路径是最短的呢，因为队列是先入先出的，而开始时已经将每个点都加入队列了，所以能保证

实现上，为了快速判断某个组合节点是否走过，需要用一个哈希表存储（这里用数组实现的）

class Solution {
    public int shortestPathLength(int[][] graph) {
        //难了，深度好像不行，广度不会做啊
        //看了题解，主要就是什么意思呢
        //一般而言，搜索过程中，只存放这个节点，遍历过了就不遍历了
        //而因为这个题中，每个位置遍历过了，还可能再走，所以还需要存放一个状态，代表当前遍历过的点的状态
        //必须这两个都相同，才表示这个点已经被遍历过了
        //还有一个不同，就是可以从任一一个节点开始广度优先搜索，所以开始时放入l个节点
        //学

        int l = graph.length;
        //int[] 三个值，当前节点值，当前遍历的状态，路径长度
        Queue<int[]> queue = new LinkedList<>();
        
        //表示一个节点是否被遍历过，方便后面查看
        boolean[][] used = new boolean[l][1 << l];
        //初始化，表示这个点上，目前这个状态遍历过了
        //把所有节点加入队列
        for(int i = 0; i < l; i++){
            queue.offer(new int[]{i, 1 << i, 0});
            used[i][1 << i] = true;
        }

        
        while(!queue.isEmpty()){
            int[] temp = queue.poll();
            int[] connect = graph[temp[0]];
            for(int i = 0; i < connect.length; i++){
                int point = connect[i];
                int mask = (temp[1] | (1 << point));
                //如果mask都是1，即都走过了，就返回此时的路径
                //可以保证此时的路径就是最短路径
                if(mask == (1 << l) - 1)
                    return temp[2] + 1;
                //如果这种状态出现过了，就跳过
                if(used[point][mask])
                    continue;
                used[point][mask] = true;
                
                queue.offer(new int[]{point, mask, temp[2] + 1});
            }
        }
        return 0;
    }
}

状态压缩动态规划

class Solution {
    public int shortestPathLength(int[][] graph) {
        //状态压缩的动态规划写一下
        
        int l = graph.length;
        //预先处理两个点之间的距离
        int[][] dis = new int[l][l];
        //如果两个点不可达，置为最大数
        for(int i = 0; i < l; i++){
            Arrays.fill(dis[i], l + 1);
        }
        //两个点之间的距离是1
        for(int i = 0; i < l; i++){
            for(int j : graph[i]){
                dis[i][j] = 1;
            }
        }
        //用弗洛伊德算法，求出两个点之间的最短路
        for(int k = 0; k < l; k++){
            for(int i = 0; i < l; i++){
                for(int j = 0; j < l; j++){
                    dis[i][j] = Math.min(dis[i][j], dis[i][k] + dis[k][j]);
                }
            }
        }

        //状态压缩动态规划，对于每一个状态mask
        //要求到达这个状态的最短路径，就是从任一个节点出发，到达这个这个状态的最短路径
        //写一下

        int[][] dp = new int[l][1 << l];
        //初始化为最大值
        for(int i = 0; i < l; i++){
            Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
        }
        //遍历所有的状态
        for(int mask = 1; mask < (1 << l); mask++){
            //如果mask中只有一个为1，那么说明是开始状态，dp为0
            if((mask & (mask - 1)) == 0){
                //找出1的位置
                int u = Integer.bitCount(mask - 1);
                //最短路劲为0
                dp[u][mask] = 0;
            }else{
                for(int u = 0; u < l; u++){
                    //如果当前状态mask中，没有u，那么跳过
                    if((mask & (1 << u)) == 0){
                        continue;
                    }
                    //如果不等于0，那么说明可以从v转移过来
                    //那转移的点就是mask中其他为1的点
                    for(int v = 0; v < l; v++){
                        //如果mask中没有v这个点，或者u和v是相等的，那么跳过
                        if(u == v || (mask & (1 << u)) == 0)
                            continue;
                        //否则转移
                        //取出u的mask
                        int mask2 = mask ^ (1 << u);
                        //从v转移到u
                        dp[u][mask] = Math.min(dp[u][mask], dp[v][mask2] + dis[v][u]);
                    }
                }
            }
        }
        int res = Integer.MAX_VALUE;
        for(int i = 0; i < l; i++){
            res = Math.min(dp[i][(1 << l) - 1], res);
        }
        return res;
    }
}

再次总结一下这个状态压缩dp，看了三叶姐所提示的状态压缩dp，又略有启发

为什么要遍历mask来转移呢？

正常的状态方程，dp[u][mask]是由与u相连的点v来转移的，即dp[v][mask2]
但是这里并不能先求出dp[v][mask2]的值，导致这样转移不能进行
为什么无法求出呢，因为存在环，所以一个dp[v][mask2]并不能保证之前已经计算好了（后面还可能转移到）
所以，这里遍历的是mask
可以选择枚举mask中的所有位1的位置，也就是u，并且由其他为1的位置转移而来，也就是v
也可以和三叶姐一样枚举mask中所有位1的位置，充当u，然后其他为0的位置，充当下一步，v；这样就行转移
大前提：用弗洛伊德算法计算出两点之间的最短路