学会5个数据分析常见定律，数据敏感度提升N个度

Posted 2021-08-29 Leo.yuan

有时候在和技术或者业务交流时，如果对方时不时蹦出个这效应，那定律，自己又恰巧没有听过，这时候只能呵呵假装明白。

其实这些概念也没有什么神秘的，今天整理了一下咱们数分领域常见的效应和定律，用通俗易懂的例子辅助解释，让大家快速理解掌握！

1.辛普森悖论
辛普森悖论指的是，在对比AB两个群体的数据，将数据拆分成多个维度时，A组在各个维度下的表现均好于B，整体A组的表现却并不一定好于B。

没看懂？来，举个例子解释下

最近英国各大高校offer都发了，结果某所高校的两个学院，法学院和文学院，在招生上被怀疑有性别歧视，我们来看一下招生情况，分析分析。

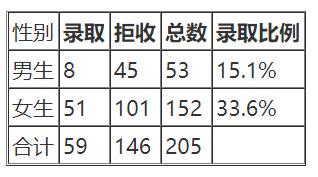
法学院招生情况

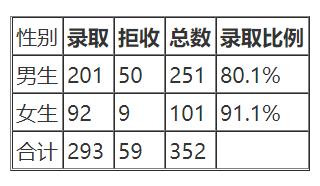
文学院招生情况

从表上录取比例数据来看，女生的录取比例都比男生高33.6%>15.1%，91.1%>80.1%

但把两个学院的数据汇总后

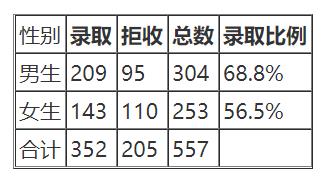
法学院、文学院数据汇总

会发现结果女生的录取比例反而比男生低，

这就是经典的辛普森悖论，即在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。

其实，“农村包围城市，武装夺取政权” 也是有类似的思想。

2、马太效应
马太效应出自圣经里的一则寓言：“凡是有的，还要加倍给他，让他多出来；没有的，就把他所有的夺过来，让他一点都没有”。通俗地解释就是 “强的越强，弱的越弱”。

马太效应在业务中非常常见。比如在推荐算法中，被判定为质量较好的用户所得到的资源就越多，这种情况也会形成反馈，得到的资源越多越会被判定为质量较好的用户，从而加剧这种效应（类似于短视频点赞越多曝光越多，曝光越多点赞越多）。

3.本福特定律
本福特定律，是说一堆从实际生活得出的数据中，以1为首位数字的数的出现机率约为总数的三成，这个定律至今没有经过一个严格的证明。

他就像是一个监控指标，当一组数据不符合本福特定律时，就有理由怀疑数据是否造假。所以此定律经常用在检测上市公司财报是否造假以及选举中是否有舞弊现象。

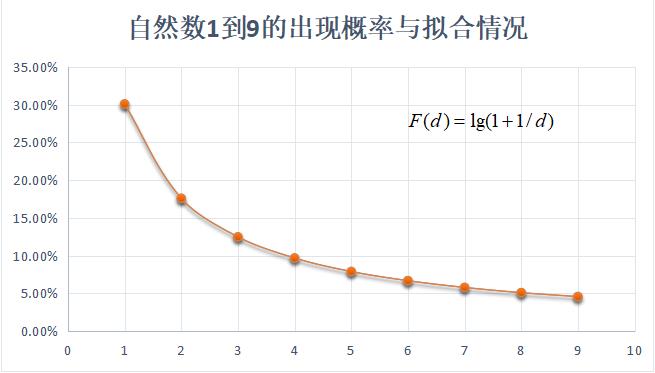
需要注意的是，它可用于检查各种数据是否有造假，但要注意使用条件：1.数据至少3000笔以上；2.不能有人为操控。

4、幸存者偏差
幸存者偏差，是优胜劣汰之后自然选择出的一个道理：未幸存者已无法发声。

人们只看到经过某种筛选而产生的结果，而没有意识到忽略了被筛选掉的人。

举个例子，大家肯定都听过这句话：“读书有什么用，我的小学同学他从小成绩一塌糊涂，初中都没念完就退学了，现在生意做得可大了，我本科毕业还不是996租着房吃着泡面。”

但，实际情况是一个班中会读书的那帮孩子日后也有生意做得不错的、也有租房吃泡面的、也有在家啃老的，可平均生活水准高于不读书的。但不读书的孩子中有一些可能欠一屁股债躲起来了、失业没有工作，这些人你看不到，你只能看到那些幸存者，生意做得可大。

5、帕累托定律
这个名字大家可能并不熟悉，但是一定听过二八定律，管理学家帕累托通过研究大量事实发现：社会上20%的人占有80%的社会财富。

比如活跃用户中仅有20%的付费用户，付费用户中20%的用户贡献了80%的收入等等。当然20%与80%只是一个统计数据，其实质讲的是 “在因和果、努力和收获之间，普遍存在着不平衡关系” ， 即不平衡关系存在的确定性和可预测性。

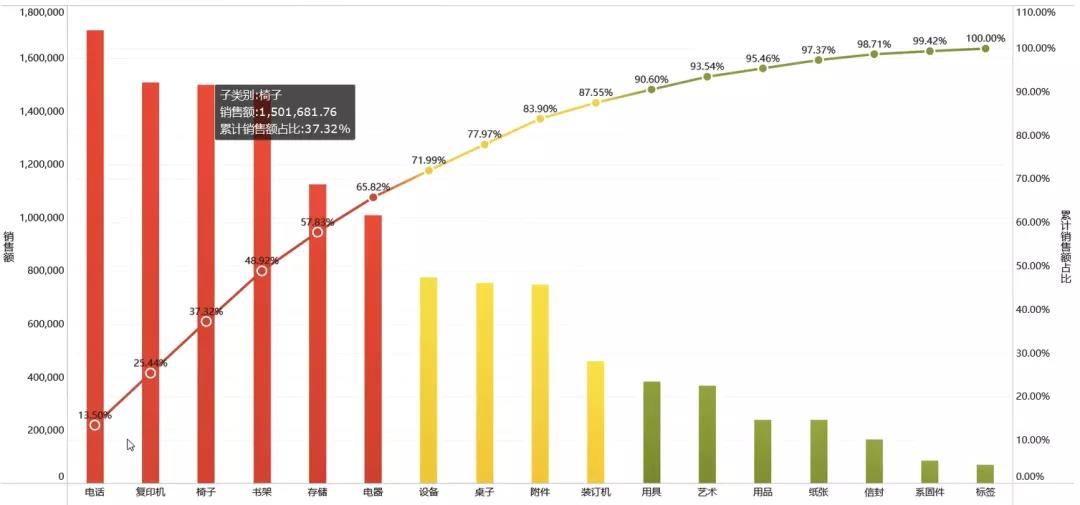
二八定律告诉我们要把精力放在更本质的事情上，不经规划地做事情很有可能会浪费80%的精力去产出20%的东西。

在数分工作中，有些同学在做分析的时候，可能经常有这种感受，跑了n个sheet的数据，结果写报告的时候，只用了四五个数据。

所以在分析的习惯是先思考产生问题的原因，并对每个可能的原因赋予相应的权重，然后以最简单方便的方法来验证各个原因，快速排除错误方向，而不是在每个原因上都做详细的解释。