Efficient Symmetric Primitives for Advanced Cryptographic Protocols (A Marvellous Contribution) 学习笔记
Posted mutourend
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Efficient Symmetric Primitives for Advanced Cryptographic Protocols (A Marvellous Contribution) 学习笔记相关的知识,希望对你有一定的参考价值。
1. 引言
Aly等人2019年论文《Efficient Symmetric Primitives for Advanced Cryptographic Protocols (A Marvellous Contribution)》。
sponge结构用于构建hash函数 from an underlying permutation by iteratively applying it to a large state。该state包含 b = r + c b=r+c b=r+c位,其中:
- r r r:为sponge rate
- c c c:为sponge capacity
可将长度变化的input,通过在每次递归过程中absorb input中的 r r r bit,hash为任意长度的output。
2. Rijndael-128 block cipher
Rijndael-128 cipher,俗称AES-128,包含了5个基础块:
- AddRoundKey
- SubBytes
- MixColumns
- ShiftRows
- ExpandKey(其中包含SubWords、AddWords、RotWords和AddConstants)
本文主要关注S-Boxes的调整(即SubBytes和SubWords)。
每个S-Box以一个字节为单位进行处理,S-Box
(
z
)
=
g
(
f
(
z
)
)
(z)=g(f(z))
(z)=g(f(z)),其中:
- f f f 函数(求倒数函数): f : F 2 8 → F 2 8 : x ↦ x 254 f:\\mathbb{F}_{2^8}\\rightarrow \\mathbb{F}_{2^8}:x\\mapsto x^{254} f:F28→F28:x↦x254,为adapted multiplicative inverse function over F 2 8 \\mathbb{F}_{2^8} F28。可抵抗differential攻击和linear攻击,同时可支持与MixColumns和ShiftRows扩散函数一起用于wide trail design strategy。【注意,有限域内有: x p − 1 m o d p ≡ 1 x^{p-1} \\mod p\\equiv 1 xp−1modp≡1,从而有倒数运算: x − 1 = x p − 2 x^{-1}=x^{p-2} x−1=xp−2。】
-
g
g
g 函数(affine多项式):
g
:
F
2
8
→
F
2
8
:
x
↦
M
x
+
b
g:\\mathbb{F}_{2}^8\\rightarrow \\mathbb{F}_2^8: x\\mapsto Mx+b
g:F28→F28:x↦Mx+b,为 SubBytes step 中的affine transformation。其中
M
∈
F
2
8
×
8
,
b
∈
F
2
8
M\\in\\mathbb{F}_2^{8\\times 8}, b\\in \\mathbb{F}_2^8
M∈F28×8,b∈F28。这种转换有助于增加S-Box结果的复杂性,以抵抗algebraic 攻击。
当affine transformation针对 F 2 \\mathbb{F}_{2} F2时,则整个S-Box可 以如下多项式表示(over F 2 8 \\mathbb{F}_{2^8} F28):
S-Box ( z ) = 0 x 05 ⋅ z 254 + 0 x 09 ⋅ z 253 + 0 x F 9 ⋅ z 251 + 0 x 25 ⋅ z 247 + 0 x F 4 ⋅ z 239 + 0 x 01 ⋅ z 223 + 0 x B 5 ⋅ z 191 + 0 x 8 F ⋅ z 127 + 0 x 63 (z) =0x05 \\cdot z^{254}+0x09\\cdot z^{253}+0xF9\\cdot z^{251}+0x25\\cdot z^{247}+0xF4\\cdot z^{239}+0x01\\cdot z^{223}+ 0xB5\\cdot z^{191} +0x8F\\cdot z^{127}+0x63 (z)=0x05⋅z254+0x09⋅z253+0xF9⋅z251+0x25⋅z247+0xF4⋅z239+0x01⋅z223+0xB5⋅z191+0x8F⋅z127+0x63
3. MiMC
MiMc的构建方式有:
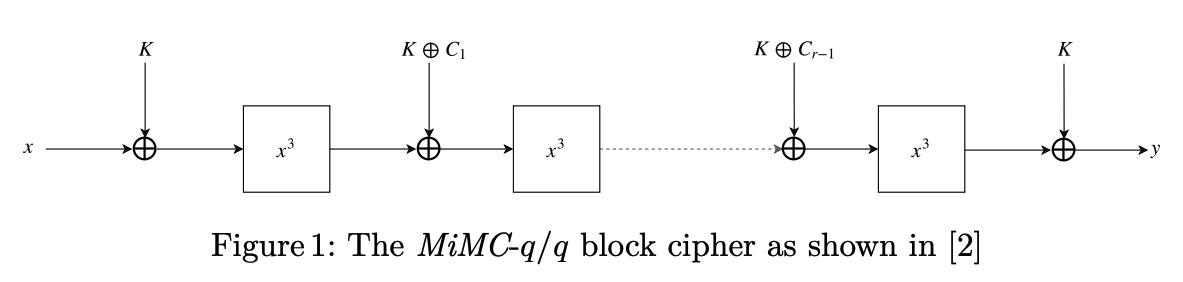
- 采用Albrecht等人2016年论文《Mimc: Efficient encryption and cryptographic hashing with minimal multiplicative complexity》中的block cipher构建,表示为MiMC-q/q:(其中
q
q
q为prime或为 prime power of 2。)在每一个round,每个state仅包含一个field element,包含一个field element in
F
\\mathbb{F}
F 会做立方运算,再与随机常量
C
i
C_i
Ci相加,每一个round插入的key
K
K
K是完全相同的。对于128位状态,需要82 rounds就足够。
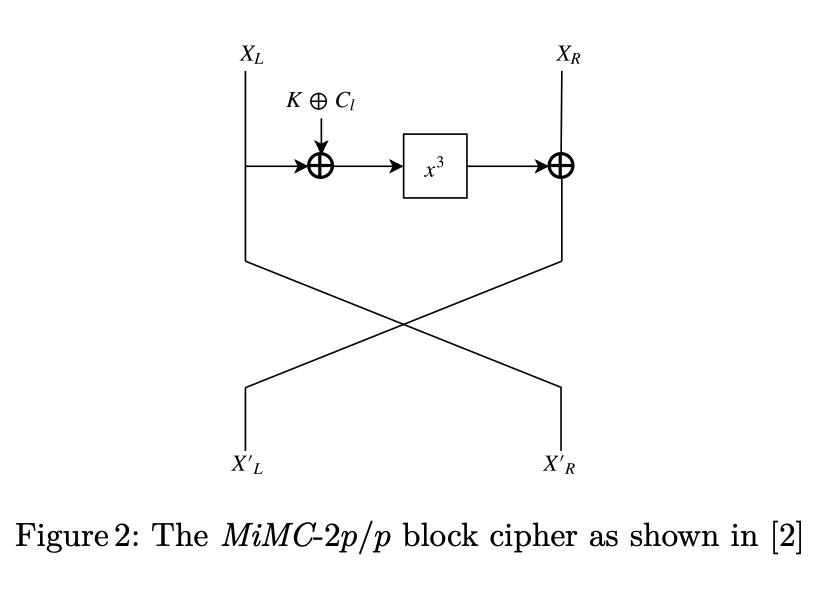
- 采用Feistel network构建,表示为MiMC-2p/p:(其中
p
p
p为prime或为 prime power of 2。)在每一个round,每个state包含2个
F
p
\\mathbb{F}_p
Fp elements,分别表示为
x
L
x_L
xL和
x
R
x_R
xR。第
l
l
l round的函数为:
x L ∣ ∣ x R ← x R + ( x L + K + C l ) 3 ∣ ∣ x L x_L||x_R\\leftarrow x_R+(x_L+K+C_l)^3||x_L xL∣∣xR←xR+(xL+K+Cl)3∣∣xL
其中 K K K为key, c l c_l cl为第 l l l round常量。对于128位状态,需164 rounds就足够。
4. Vision
采用Rijndael-128 block cipher,针对的field为
F
2
n
/
m
m
\\mathbb{F}_{2^{n/m}}^{m}
F2n/mm,具有
n
n
n-bit staten、
n
n
n-bit key和
n
n
n bits security。
Vision的最小round数为10,推荐round数为
2
⌈
n
/
5.5
m
⌉
2\\left \\lceil n/5.5m \\right \\rceil
2⌈n/5.5m⌉。
Vision中:
-
f
f
f 函数(求倒数函数)为:
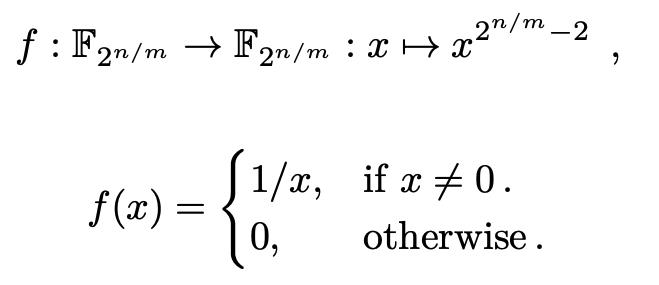
g g g 函数(affine多项式)为:奇数步为 B − 1 ( x ) B^{-1}(x) B−1(x),偶数步为 B ( x ) B(x) B(x)。
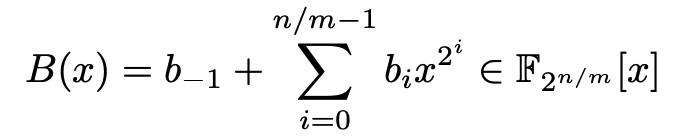
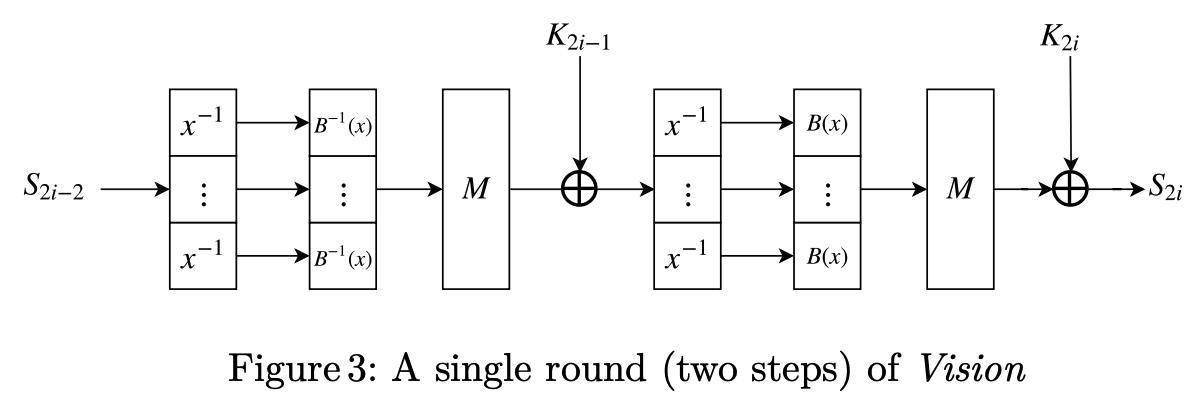
key schedule:是指基于一个key派生出所有round keys的算法。(calculates all the round keys from the key)。
Vision的key schedule为:
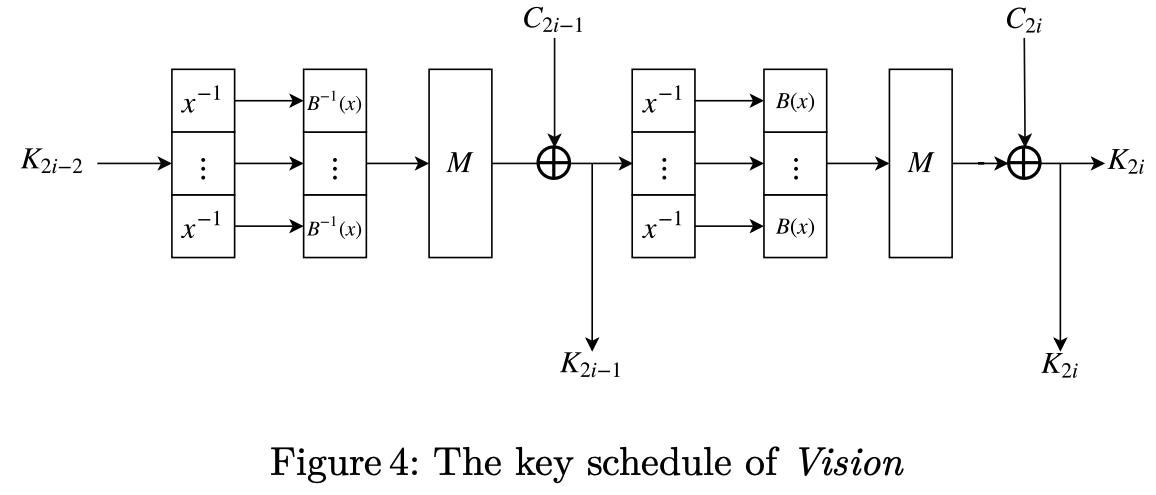
详细的Vision算法实现为:

5. Rescue
与Vision类似,但是其针对的域为 F p \\mathbb{F}_p Fp,而不是 F 2 n / m \\mathbb{F}_{2^{n/m}} F2Efficient GAN
Efficient-Net基于Efficient-Net效率网的目标识别算法的MATLAB仿真——详细版