动态规划悬线法

Posted 2021-08-23 御城变

悬线法是用来处理子矩阵相关的问题，在一个矩形中寻找一个最大的满足条件的矩阵
悬线法的基本思路，维护三个数组，l[N][N],r[N][N],up[N][N]。
l[N][N]:用来记录在当前这个位置满足条件的左边界，也就是可以往左延伸到哪一列。
r[N][N]:用来记录当前和这个位置满足条件的右边界，也就是可以往右延伸到哪一列
up[N][N]:用来记录当前这个位置满足条件高度，也就是可以往上延伸到哪个位置

eg：

P1169 [ZJOI2007]棋盘制作.
国际象棋是世界上最古老的博弈游戏之一，和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想，棋盘是一个8 \\times 88×8大小的黑白相间的方阵，对应八八六十四卦，黑白对应阴阳。
而我们的主人公小Q，正是国际象棋的狂热爱好者。作为一个顶尖高手，他已不满足于普通的棋盘与规则，于是他跟他的好朋友小W决定将棋盘扩大以适应他们的新规则。
小Q找到了一张由N \\times MN×M个正方形的格子组成的矩形纸片，每个格子被涂有黑白两种颜色之一。小Q想在这种纸中裁减一部分作为新棋盘，当然，他希望这个棋盘尽可能的大。
不过小Q还没有决定是找一个正方形的棋盘还是一个矩形的棋盘（当然，不管哪种，棋盘必须都黑白相间，即相邻的格子不同色），所以他希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积，从而决定哪个更好一些。
于是小Q找到了即将参加全国信息学竞赛的你，你能帮助他么？

对这个三个矩阵进行操作后就可以的得到这个子矩阵的长和宽
长为

int len=r[i][j]-l[i][j]+1;

宽为

up[i][j]

以此不断迭代可以得到最大的子矩阵面积

 ans2=max(ans2,up[i][j]*len);

测试样例：

3 7
0 0 1 0 1 0 1
1 0 1 0 1 1 0
1 0 1 0 1 0 1

#include<bits/stdc++.h>
using namespace std;
const int N=2010;
typedef long long ll;

int ma[N][N],l[N][N],r[N][N],up[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&ma[i][j]);
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            l[i][j]=j;
            r[i][j]=j;
            up[i][j]=1;            
        }
    }    
    for(int i=1;i<=n;i++)
    {
        for(int j=2;j<=m;j++)
        {
            if(ma[i][j]!=ma[i][j-1])
            {
                l[i][j]=l[i][j-1];
            }  
        }
        for(int j=m-1;j>=0;j--)
        {
            if(ma[i][j]!=ma[i][j+1])
            {
                r[i][j]=r[i][j+1];
            }
        }
    }

首先需要根据定义求出l[N][N],r[N][N],up[N][N]三个矩阵

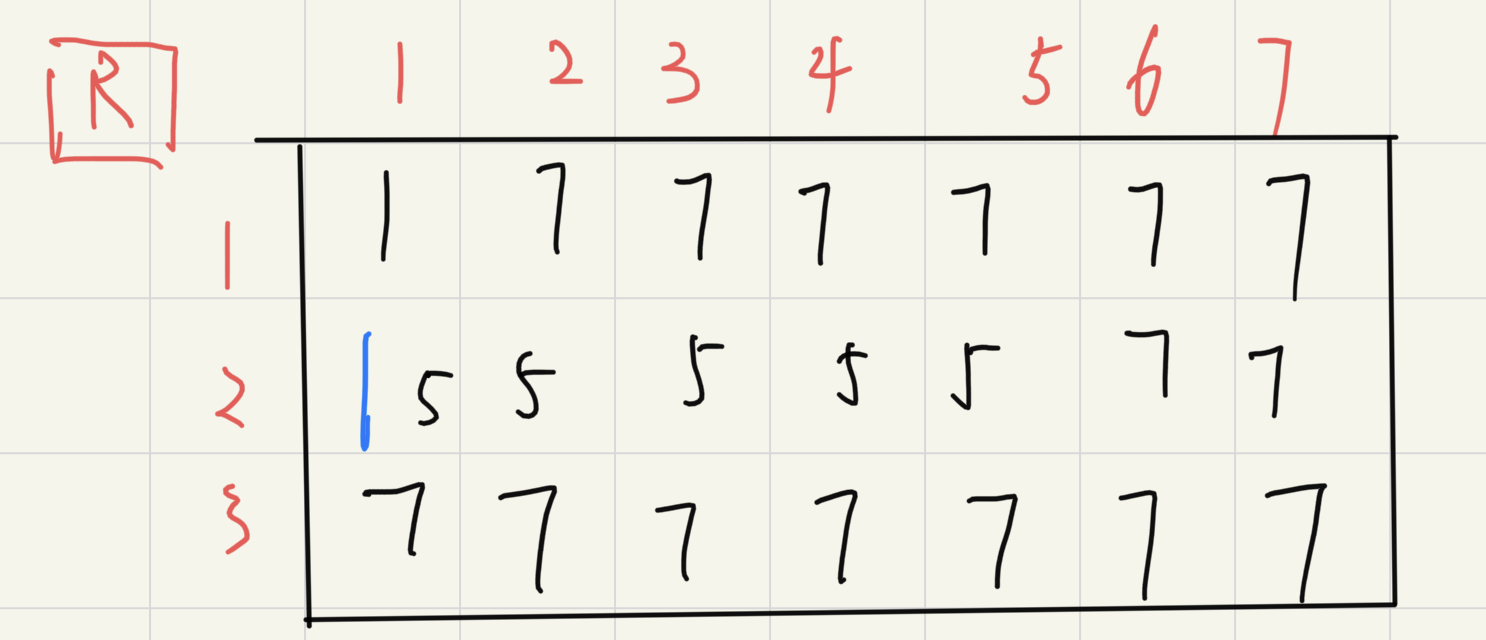
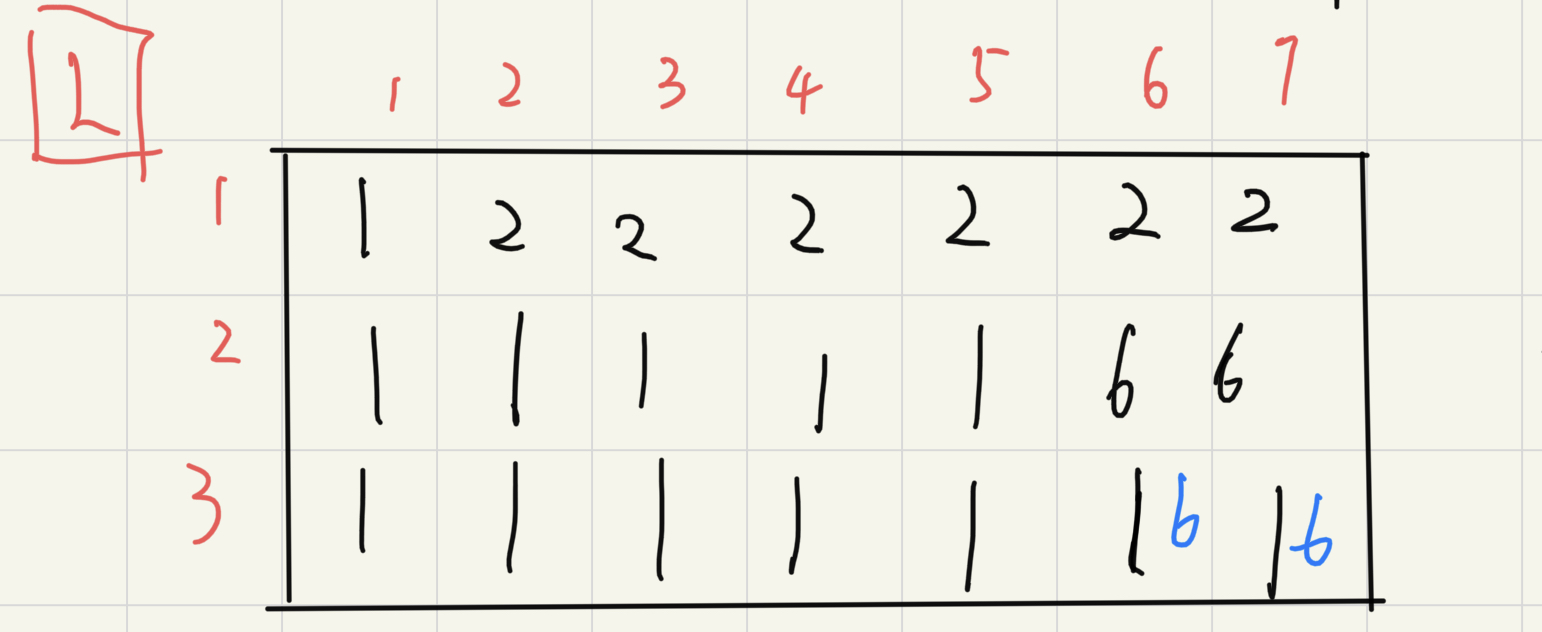
    int ans1=0,ans2=0;
    for(int i=1;i<n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(i==1)continue;
            if(ma[i][j]!=ma[i-1][j])
            {
                up[i][j]=up[i-1][j]+1;
                l[i][j]=max(l[i][j],l[i-1][j]);
                r[i][j]=min(r[i][j],r[i-1][j]);
            }
            int len=r[i][j]-l[i][j]+1;
            ans1=max(ans1,min(up[i][j],len));
            ans2=max(ans2,up[i][j]*len);
        }   
    }
    cout<<ans1*ans1<<endl;
    cout<<ans2<<endl;
    return 0;
}