数据结构(12)---二叉树之顺序结构

Posted 2021-08-21 李憨憨_

二叉树

---

文章目录

• 二叉树
• 二叉树的顺序结构及实现
• • 二叉树的顺序结构
  • 堆的概念及结构
  • 堆的创建
  • • 堆向下调整算法
  • 建堆的过程
  • 堆的插入
  • 堆的删除
  • 堆的排序
  • 堆的代码实现

---

二叉树的顺序结构及实现

二叉树的顺序结构

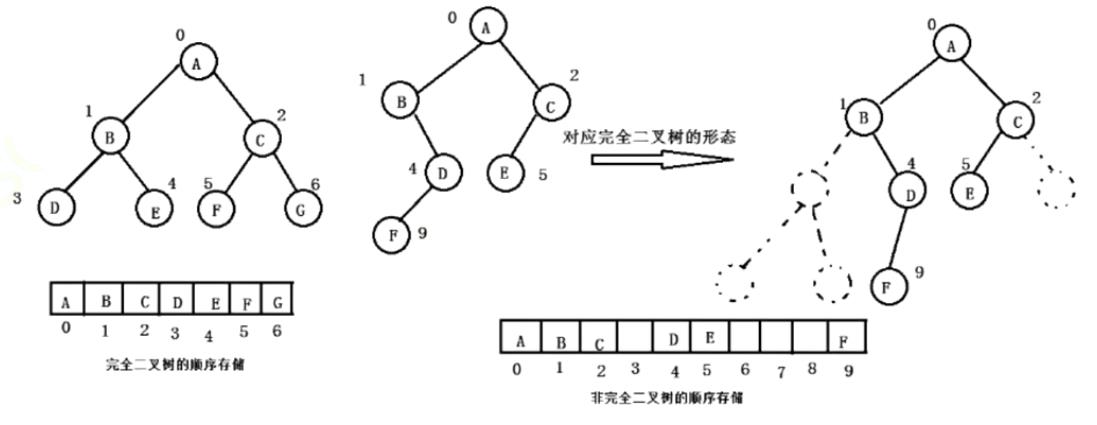
普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

堆的概念及结构

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
 堆的性质：
   堆中某个节点的值总是不大于或不小于其父节点的值；
   堆总是一棵完全二叉树。

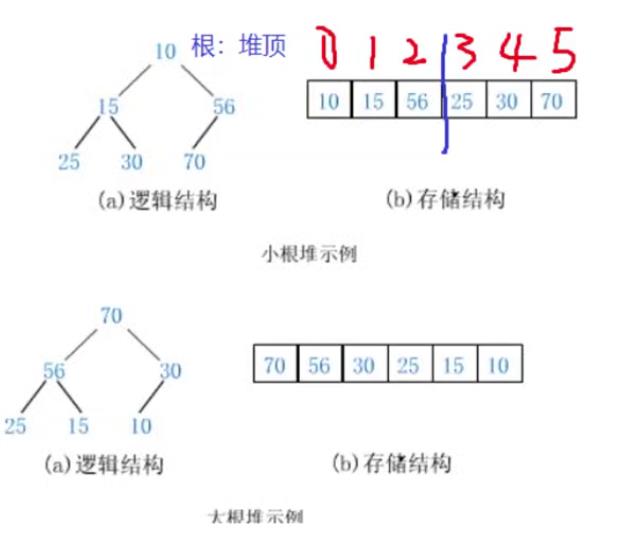
如果是小根堆, 根节点是所有节点中的最小值;
如果是大根堆, 根节点是所有节点中的最大值;

堆的创建

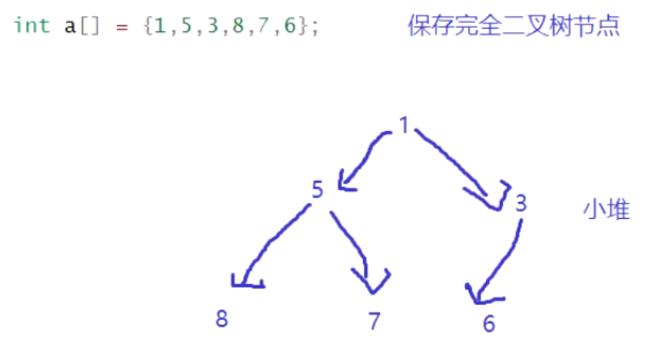
堆向下调整算法

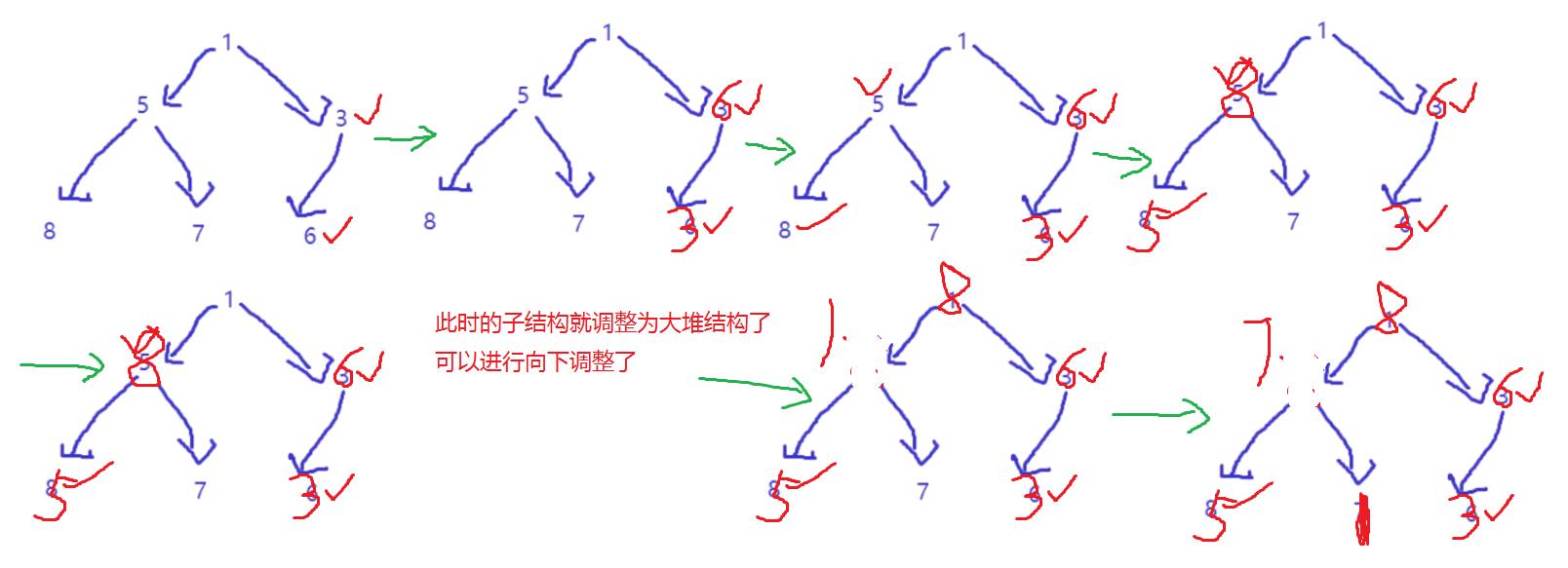
现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

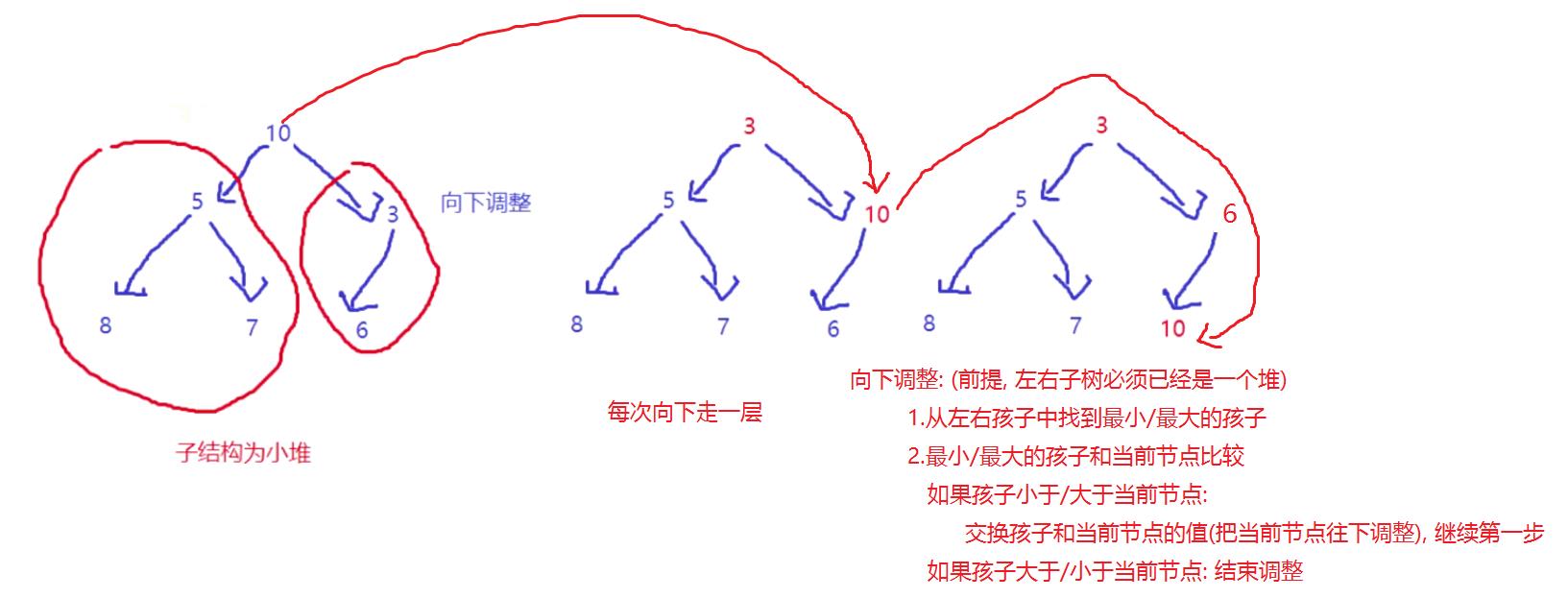
建堆的过程

堆的插入

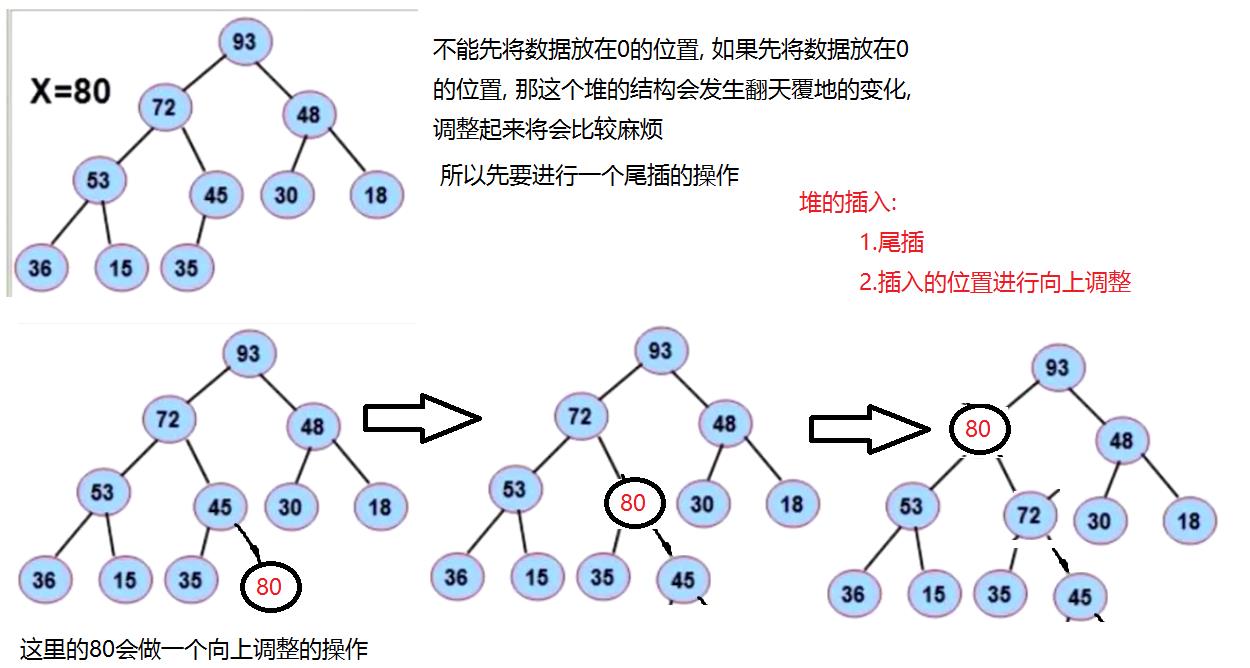
而且尾插效率是最高的, 不需要挪动元素

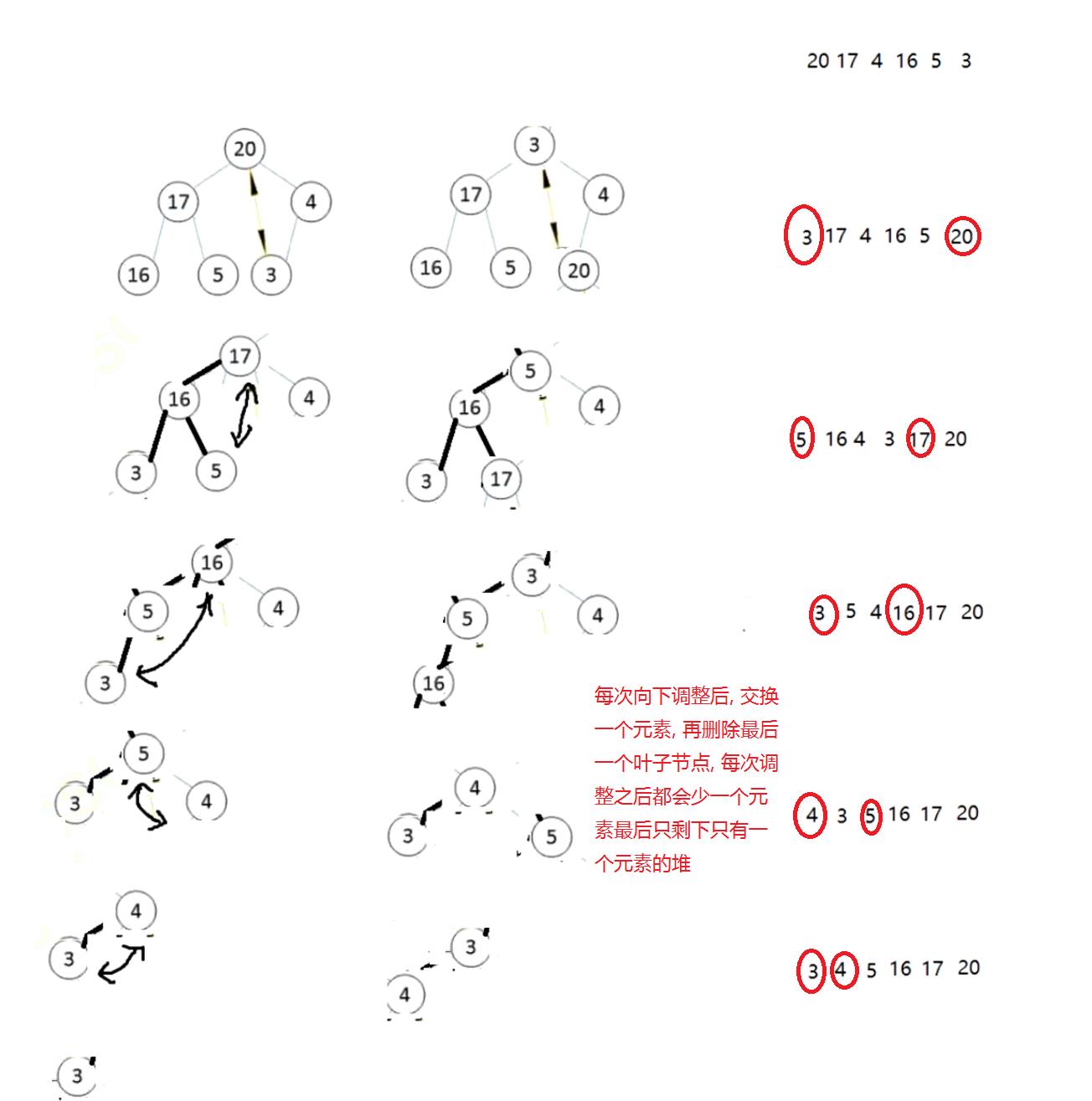
堆的删除

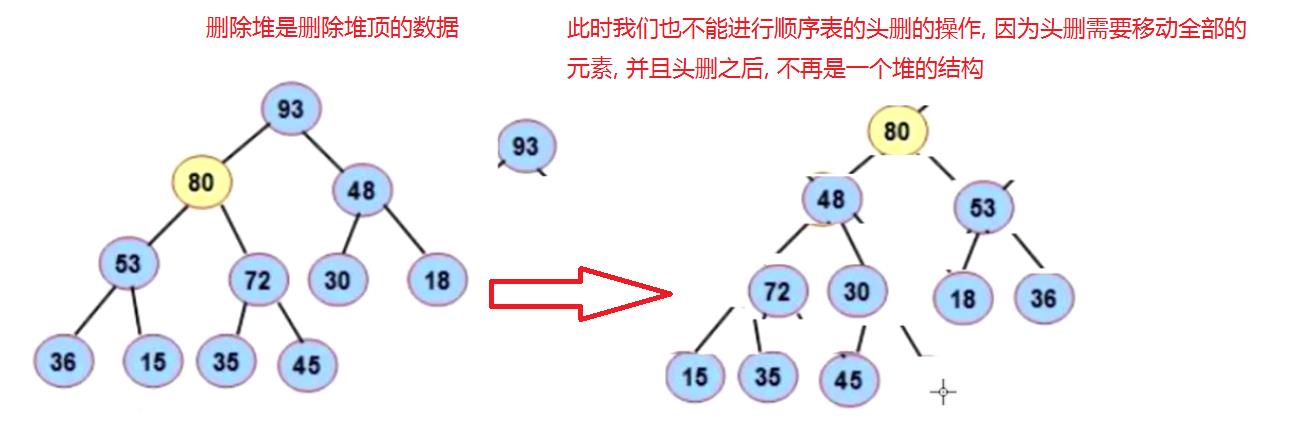
堆的排序

堆的代码实现

#include <stdio.h>
#include <stdlib.h>

//假设小堆
typedef int HDataType;

typedef struct heap
{
	HDataType* _data;
	int _size;
	int _capacity;
}heap;

//堆的初始化
void heapInit(heap* hp)
{
	if (hp == NULL)
		return;
	hp->_data = NULL;
	hp->_size = hp->_capacity = 0;
}

//检查容量
void checkCapacity(heap* hp)
{
	if (hp->_size == hp->_capacity)
	{
		int newC = hp->_capacity == 0 ? 1 : 2 * hp->_capacity;
		hp->_data = (HDataType*)realloc(hp->_data, sizeof(HDataType) * newC);
		hp->_capacity = newC;
	}
}

//交换
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

//堆的插入
void heapPush(heap* hp, HDataType val)
{
	if (hp == NULL)
		return;
	//检查容量
	checkCapacity(hp);
	//尾插
	hp->_data[hp->_size++] = val;
	//向上调整
	shiftUp(hp->_data, hp->_size, hp->_size - 1);
}

//堆的删除
void heapPop(heap* hp)
{
	if (hp->_size > 0)
	{
		//交换
		Swap(&hp->_data[0], &hp->_data[hp->_size - 1]);
		//尾删
		hp->_size--;
		//从堆顶位置开始向下调整
		shiftDown(hp->_data, hp->_size, 0);
	}
}

//获取堆顶元素
HDataType heapTop(heap* hp)
{
	return hp->_data[0];
}

//堆的判空
int heapEmpty(heap* hp)
{
	if (hp == NULL || hp->_size == 0)
		return 1;
	else
		return 0;
}

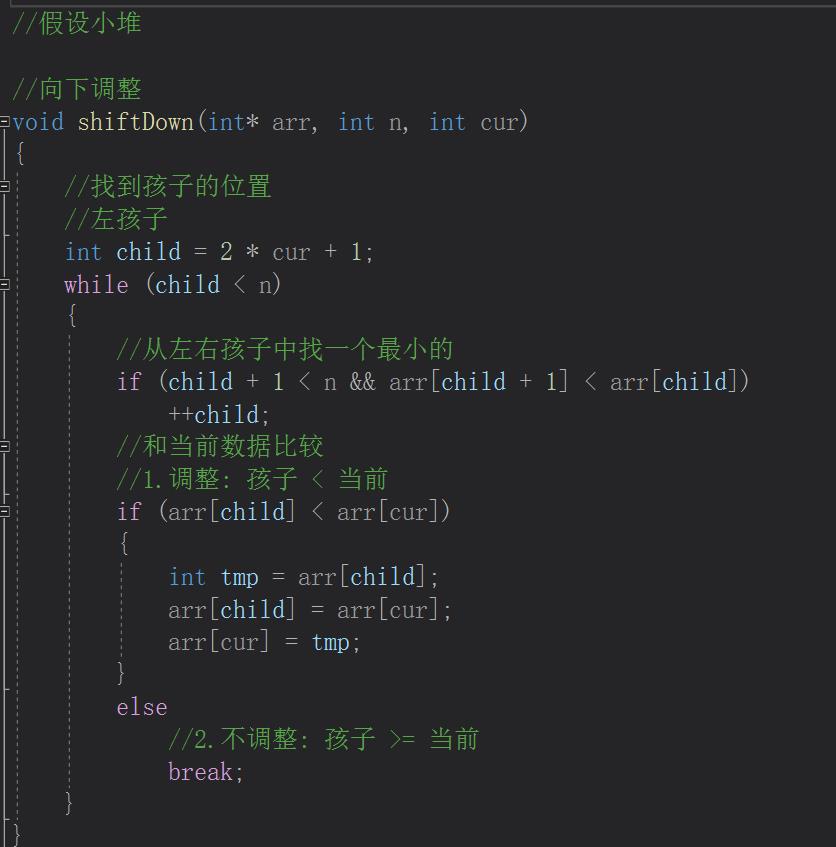
//向下调整
void shiftDown(int* arr, int n, int cur)
{
	//找到孩子的位置
	//左孩子
	int child = 2 * cur + 1;
	while (child < n)
	{
		//从左右孩子中找一个最小的
		if (child + 1 < n && arr[child + 1] < arr[child])
			++child;
		//和当前数据比较
		//1.调整: 孩子 < 当前
		if (arr[child] < arr[cur])
		{
			int tmp = arr[child];
			arr[child] = arr[cur];
			arr[cur] = tmp;
		}
		else
			//2.不调整: 孩子 >= 当前
			break;
	}
}

//向上调整
void shiftUp(int* arr, int n, int cur)
{
	//和父节点进行比较
	int parent = (cur - 1) / 2;
	while (cur > 0)
	{
		if (arr[cur] < arr[parent])
		{
			int tmp = arr[cur];
			arr[cur] = arr[parent];
			arr[parent] = tmp;
			//更新位置
			cur = parent;
			parent = (cur - 1) / 2;
		}
		else
			break;
	}
}