数据结构之哈希表
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之哈希表相关的知识,希望对你有一定的参考价值。
文章目录
一:哈希的基本概念
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素的时候,必须要经过关键码的多次比较,搜索的效率取决于比较的次数
- 顺序查找时间复杂度 O ( N ) O(N) O(N)
- 平衡树的则为树的高度,即 O ( l o g 2 N ) O(log_{2}N) O(log2N)
理想的查找应该是这样子的:不经过任何比较,一次直接就可以从表中找到待查找的元素。如果构造一种存储结构,通过某种函数(哈希函数)使元素的存储位置与它的关键码之间建立一一映射的关系,那么时间复杂度可以达到 O ( 1 ) O(1) O(1)
例如:有一个数据集合{1,7,6,4,5,9}
哈希函数设置为
h
a
s
h
(
k
e
y
)
=
k
e
y
%
c
a
p
a
c
i
t
y
hash(key)=key \\% capacity
hash(key)=key%capacity
对每个数据分别定址,你可以理解代入
f
(
x
)
f(x)
f(x),算得的函数值就是地址

二:常见哈希函数
(1)直接定址法 ( 常 用 ) _{(常用)} (常用)
取关键字的某个线性函数为散列地址,即
H
a
s
h
(
K
e
y
)
=
A
∗
K
e
y
+
B
Hash(Key)=A*Key+B
Hash(Key)=A∗Key+B
优点: 简单、快速、均匀
缺点: 需要事先知道关键字的分布情况
适用情形: 适合查找比较小且连续的情况
比如LeetCode387:字符串中的第一个唯一字符展现的就是直接定址,字母与数组下标一一映射,映射函数就是每个字母与小写字母 a a a的相对位置,地址就是数组下标
class Solution {
public:
int firstUniqChar(string s)
{
int count[26]={0};
for(int i=0;i<s.size();i++)
{
count[s[i]-'a']++;
}
for(int i=0;i<s.size();i++)
{
if(count[s[i]-'a']==1)
return i;
}
return -1;
}
};
(2)除留余数法 ( 常 用 ) _{(常用)} (常用)
设散列表中允许的地址数为
m
m
m ,取一个不大于m,但是最接近或者等于
m
m
m的质数
p
p
p作为除数,按照哈希函数
H
a
s
h
(
K
e
y
)
=
k
e
y
%
p
(
p
≤
m
)
Hash(Key)=key\\%p(p\\leq m)
Hash(Key)=key%p(p≤m)
将关键码转换为哈希地址
这种方法最大的缺陷就是会产生哈希冲突——不同的关键字映射到了相同的地址

(3)平方取中法 ( 了 解 ) _{(了解)} (了解)
取关键字平方后的中间几位作为 H a s h Hash Hash地址。一个数平方后的中间几位数和数的每一位都相关,由此得到的Hash地址随机性会更大,适用于不知道关键字的分布,而位数又不是很大的情况
比如关键字 1234 1234 1234,其平方后的结果为 1522756 1522756 1522756,可以取227作为哈希地址
(4)数字分析法 ( 了 解 ) _{(了解)} (了解)
设有 n n n个 d d d位数,每一位可能有 r r r种不同的符号取值,这 r r r种不同的符号在各个位上出现的频率不一定相同,可能在某些位上分布较为均匀,每种符号出现的机会均等,而在某系位上分布不均匀只有某种符号经常出现。可以根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。比较适合于处理关键字位数较大的情况,以及事先知道关键字的分布情况
生活中常见的就是手机号

(5)折叠法 ( 了 解 ) _{(了解)} (了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短一点),然后这几部分重叠求和,并按照散列表表长,取后几位作为散列地址。
比较适合于事先不知道关键字的分布,以及关键字位数较多的情况。
(6)随机数法 ( 了 解 ) _{(了解)} (了解)
选择一个随机数,取关键字的随机函数值作为其哈希地址,即
H
(
K
e
y
)
=
r
a
n
d
o
m
(
k
e
y
)
H(Key)=random(key)
H(Key)=random(key)
其中
r
a
n
d
o
m
random
random为随机函数
三:解决Hash冲突
前面说过,如果哈希函数选择的不合适,经常会出现不同的关键字被映射在同一个地址的情况。如果出现了这种情况,我们就必须解决冲突。
(1)闭散列(开放定址法)
当产生哈希冲突时,如果哈希表没有被装满,那么哈希表中必然还会有空的位置,所以开放定址法就会不断寻找空的位置,找到空的位置将关键字塞入进去。根据找的方法不同,开放定址法又分为线性探测法和二次探测法
A:线性探测法
从没有发生冲突的位置开始,依次向后探测,直到找到下一个空的位置为止。
比如下面哈希表没有冲突

接着来了一个新的关键字,根据哈希函数,它将会被映射在地址为4的位置,但是4的位置已经有关键字了,所以会产生冲突。采用线性探测法就会从冲突开始的位置,依次向后探测,直到找到空位置,如果找到最后,将会返回开头重新找起
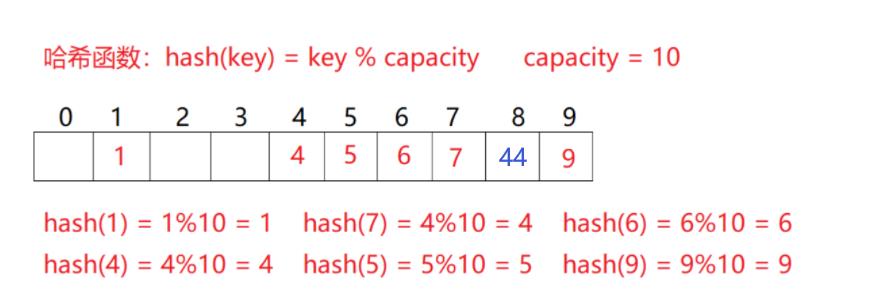
但是这里产生了一个很大问题:散列表是用来查找的,我们查找是根据关键字依靠散列函数定位的,44原本的地址就是下标4,但是由于产生了冲突,其最新的位置变为了8,那么这样的话根据散列函数算得的位置就错误了。
所以在这种情况下查找,如果第一次算得的哈希地址处的关键字和预料的不一样,那么并不能直接说明该关键字并不在散列表中,因此一旦查找不一致,应该从下一个位置开始依次比对,如果这个过程中比对正确了,那么返回最新的位置;如果饶了一圈最终还是回到了当初的位置,那么可以说明该关键字并不在散列表中。
线性探测有点显而易见,非常简单易于实现;但是缺点也很大,就是数据容易产生堆积,这种堆积会引发多米诺效应,如果堆积太大,大大降低效率
B:二次探测法
二次探测法指的并不是线性探测两次。线性探测解决冲突最大的弊端就是找空位置的时候是挨个挨个去找的,而二次探测法找下一个位置的方法为:
H
i
=
(
H
0
+
i
2
)
%
m
)
H_{i}=(H_{0}+i^{2})\\%m )
Hi=(H0+i2)%m)
其中 i = 1 , 2 , 3 , , , , i=1,2,3,,,, i=1,2,3,,,,, H 0 H_{0} H0是通过散列函数 H a s h ( x ) Hash(x) Hash(x)对元素的关键码$ K e y 进 行 计 算 得 到 的 地 址 , Key进行计算得到的地址, Key进行计算得到的地址,m$为表的大小
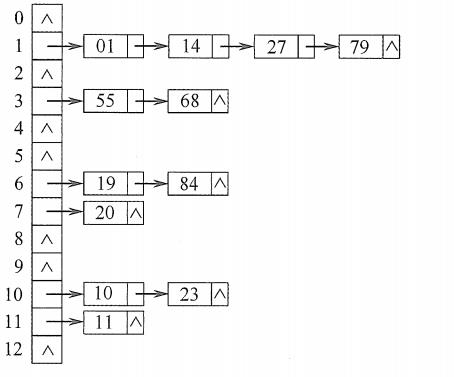
(2)开散列(链地址法)
开散列首先会对关键字集合用散列函数计算散列地址,具有相同地址的关键字会归于同一个子集合,每一个子集合称之为一个桶,各个桶中的元素通过一个单链表链接起来,可链表的头结点存储在哈希表中
以上是关于数据结构之哈希表的主要内容,如果未能解决你的问题,请参考以下文章