[DataStructure]非线性数据结构之哈希表二叉树及多叉树 Java 代码实现
Posted Spring-_-Bear
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[DataStructure]非线性数据结构之哈希表二叉树及多叉树 Java 代码实现相关的知识,希望对你有一定的参考价值。
非线性数据结构
数据结构中线性结构指的是数据元素之间存在着 “一对一” 的线性关系的数据结构。如
(a1,a2,a3,.....,an)a1为第一个元素,an为最后一个元素,此集合即为一个线性结构的集合。相对应于线性结构,非线性结构的逻辑特征是一个结点元素可能对应多个直接前驱和多个后继
一、哈希表
1. 哈希表定义
- 哈希表(
Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表- 哈希函数:直接寻址法、数字分析法、平方取中法、折叠法、随机数法、除留余数法
- 处理冲突的方法:开放寻址法、再散列法、链地址法(拉链法)、建立一个公共溢出区
2. 哈希表 java 代码实现
/**
* @author Spring-_-Bear
* @datetime 2022/3/15 9:26
*/
public class HashTable
private final LinkedList[] table;
private final int size;
public HashTable(int size)
this.size = size;
table = new LinkedList[size];
for (int i = 0; i < size; i++)
table[i] = new LinkedList();
/**
* 根据 val 查找节点信息
*
* @param val val
* @return EmployeeNode
*/
public LinkedList.ListNode find(int val)
int index = hash(val);
return table[index].find(val);
/**
* 从哈希表中删除节点
*
* @param id id
*/
public void delete(int id)
int index = hash(id);
table[index].delete(id);
/**
* 将节点添加到哈希表链表中
*
* @param node 节点
*/
public void add(LinkedList.ListNode node)
int index = hash(node.val);
table[index].add(node);
/**
* 遍历哈希表
*/
public void list()
for (int i = 0; i < size; i++)
System.out.print(i);
table[i].list();
/**
* 哈希函数:除留余数法
*
* @param val 节点 val
* @return node 应位于 hash 表中的位置
*/
public int hash(int val)
/*
* 除留余数法:取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址,
* 即 H(key) = key MOD p, p <= m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。
* 对 p 的选择很重要,一般取素数或 m,若 p 选的不好,容易产生同义词
*/
return val % 7;
class LinkedList
private ListNode head = null;
public static class ListNode
public int val;
public ListNode next;
public ListNode(int val)
this.val = val;
@Override
public String toString()
return "ListNode" +
"val=" + val +
'';
/**
* 尾插法添加节点
*
* @param node 节点
*/
public void add(ListNode node)
if (head == null)
head = node;
return;
ListNode cur = head;
while (cur.next != null)
cur = cur.next;
cur.next = node;
/**
* 打印链表
*/
public void list()
ListNode cur = head;
while (cur != null)
System.out.println(cur);
cur = cur.next;
/**
* 根据 val 在链表中查找节点
*
* @param val val
* @return ListNode
*/
public ListNode find(int val)
ListNode cur = head;
while (cur != null && cur.val != val)
cur = cur.next;
return cur;
/**
* 根据 val 删除链表中的对应节点(不带头节点)
*
* @param val val
* @return ListNode
*/
public ListNode delete(int val)
if (head == null)
return null;
ListNode temp;
ListNode current = head;
// 删除头节点且头节点后无节点
if (head.val == val && head.next == null)
temp = current;
head = null;
return temp;
// 删除头节点且头节点后仍有节点
if (head.val == val)
temp = current;
head = current.next;
return temp;
// 找到需要删除的节点的前一个节点
while (current.next != null && current.next.val != val)
current = current.next;
// 让当前节点指向当前节点的下下个节点或指向 null
temp = current.next;
if (current.next.next != null)
current.next = current.next.next;
else
current.next = null;
return temp;
二、二叉树
1. 二叉树的定义
- 二叉树(
binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树- 满二叉树:如果一棵二叉树只有度为
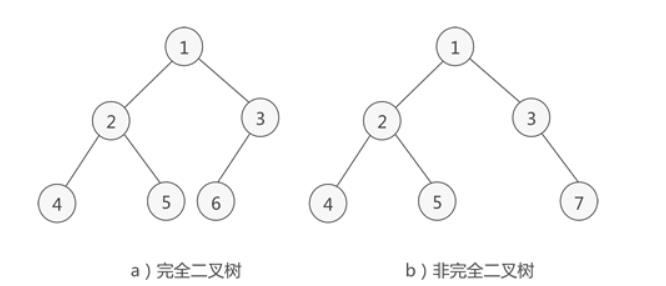
0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树(二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树)- 完全二叉树:深度为
k,有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时,称为完全二叉树(如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树)- 节点的度:一个节点拥有子树的数目称为节点的度
- 分支节点:也称为非终端节点,度不为零的节点称为非终端节点
- 树的度:树中所有节点的度的最大值
- 节点的层次:从根节点开始,假设根节点为第
1层,根节点的子节点为第2层,依此类推,如果某一个节点位于第L层,则其子节点位于第L+1层- 树的深度:也称为树的高度,树中所有节点的层次最大值称为树的深度
- 森林:由
m(m≥0)棵互不相交的树构成一片森林。如果把一棵非空的树的根节点删除,则该树就变成了一片森林,森林中的树由原来根节点的各棵子树构成
/**
* @author Spring-_-Bear
* @datetime 2022/3/15 10:59
*/
public class BinaryTree
public static class TreeNode
private final int id;
private final String name;
public TreeNode left;
public TreeNode right;
public TreeNode(int id, String name)
this.id = id;
this.name = name;
@Override
public String toString()
return "TreeNode" +
"id=" + id +
", name='" + name + '\\'' +
'';
2. 先序遍历二叉树(根->左->右)
/**
* 先序遍历
*
* @param root 根节点
*/
public void preOrder(TreeNode root)
System.out.println(root);
// 递归向左子树先序遍历
if (root.left != null)
preOrder(root.left);
// 递归向右子树先序遍历
if (root.right != null)
preOrder(root.right);
3. 中序遍历二叉树(左->根->右)
/**
* 中序遍历
*
* @param root 父节点
*/
public void midOrder(TreeNode root)
if (root.left != null)
midOrder(root.left);
System.out.println(root);
if (root.right != null)
midOrder(root.right);
4. 后序遍历二叉树(左->右->根)
/**
* 后序遍历
*
* @param root 父节点
*/
public void postOrder(TreeNode root)
if (root.left != null)
postOrder(root.left);
if (root.right != null)
postOrder(root.right);
System.out.println(root);
5. 前序查找
/**
* 前序查找
*
* @param root 根节点
* @param id 要查找的节点 id
* @return TreeNode 或 null
*/
public TreeNode preSearch(TreeNode root, int id)
if (root.id == id)
return root;
// 判断当前父节点的左子节点是否为空,不为空则递归前序查找
TreeNode treeNode = null;
if (root.left != null)
treeNode = preSearch(root.left, id);
if (treeNode != null)
return treeNode;
// 在根节点的左子树未找到,判断当前父节点的右子节点是否为空,不为空则递归前序查找
if (root.right != null)
treeNode = preSearch(root.right, id);
return treeNode;
6. 删除节点
/**
* 删除指定 id 的节点,并将节点返回
*
* @param root 父节点
* @param id id
* @return TreeNode 或 null
*/
public TreeNode delete(TreeNode root, int id)
TreeNode treeNode = null;
// 父节点为空返回 null
if (root == null)
return null;
// 父节点的子节点为空,判断父节点是否是目标节点
if (root.left == null && root.right == null)
return root.id == id ? root : null;
// 父节点的左子节点是目标节点
if (root.left != null && root.left.id == id)
treeNode = root.left;
root.left = null;
return treeNode;
// 父节点的右子节点是目标节点
if (root.right != null && root.right.id == id)
treeNode = root.right;
root.right = null;
return treeNode;
if (root.left != null)
// 向左递归删除目标节点
treeNode = delete(root.left, id);
if (root.right != null)
// 向右递归删除目标节点
treeNode = delete(root.right, id);
return treeNode;
7. 先序遍历数组
顺序二叉树通常只考虑完全二叉树
- 第 n 个元素的左子节点在顺序数组中的下标为
2 * n + 1- 第 n 个元素的右子节点在顺序数组中的下标为
2 * n + 2- 第 n 个元素的父节点在顺序数组中的下标为
(n - 1) / 2
/**
* 以二叉树前序遍历的方式遍历数组,
* index 初始值为 0
*
* @param array 数组
*/
public void preOrderArray(int[] array, int index)
if (array == null || array.length == 0)
return;
// 输出当前下标元素
System.out.print(array[index] + " ");
// 向左递归遍历
if (2 * index + 1 < array.length)
preOrderArray(array, 2 * index + 1);
// 向右递归遍历
if (2 * index + 2 < array.length)
preOrderArray(array, 2 * index + 2);
三、线索化二叉树
1. 线索化二叉树的定义
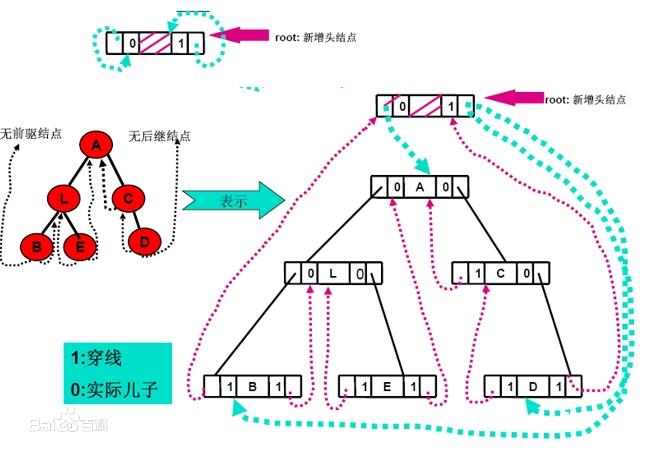
- 在二叉树的结点上加上线索的二叉树称为线索二叉树,对二叉树以某种遍历方式(如先序、中序、后序或层次等)进行遍历,使其变为线索二叉树的过程称为对二叉树进行线索化
n个节点的二叉链表中含有n + 1个空指针域(2 * n - (n - 1) = n + 1)。利用二叉链表中的空指针域,存放指向该结点在某种遍历次序下的前驱节点和后继节点的指针(这种附加的指针称为 “线索”)
/**
* @author Spring-_-Bear
* @datetime 2022/3/16 15:51
*/
public class ThreadedBinaryTree
/**
* 进行线索化时当前节点的上一个节点
*/
private TreeNode pre;
public static class TreeNode
private final int val;
public TreeNode left;
public TreeNode right;
/**
* 左指针类型:true - 当前节点左指针指向孩子节点
*/
boolean isLeftChild = true;
/**
* 右指针类型:true - 当前节点右指针指向孩子节点
*/
boolean isRightChild = true;
public TreeNode(int val)
this.val = val;
@Override
public String toString()
return "TreeNode" +
"val=" + val +
'';
2. 中序线索化二叉树
/**
* 中序线索化二叉树
*
* @param cur 二叉树当前节点
*/
public void midThreaded(TreeNode cur)
if (cur == null)
return;
// 线索化左子树
midThreaded(cur.left);
// 线索化当前节点,当前节点左指针为空,指向前驱节点
if (cur.left == null)
cur.left = pre;
cur.isLeftChild = false;
// 中序遍历的情况下无法知道当前节点的后继节点是什么,
// 所以将 cur 的后继关系留给 pre 处理
if (pre != null && pre.right == null)
pre.right = cur;
pre.isRightChild = false;
// 当前节点的前一个节点后移
pre = cur;
// 线索化右子树
midThreaded(cur.right);
3. 遍历中序线索化后的二叉树
/**
* 遍历中序线索化后的二叉树
*
* @param root 根节点
*/
public void midTraverseThreaded(TreeNode root)
if (root == null)
return;
TreeNode cur = root;
while (cur != null)
// 循环遍历直到找到左子树的最左节点
while (cur.isLeftChild)
cur = cur.left;
System.out.println(cur);
// 根据当前节点的后继节点继续遍历(右指针不指向孩子节点)
while (!cur.isRightChild)
cur = cur.right;
System.out.println(cur);
// 当前节点后移,重新判断
cur = cur.right;
四、哈夫曼树
1. 哈夫曼树的定义
- 给定
N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近- 哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为
0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)

2. 哈夫曼树的创建
/**
* @author Spring-_-Bear
* @datetime 2022/3/18 10:24
*/
public class HuffmanTree
public static class TreeNode implements Comparable<TreeNode>
private final int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val)
this.val = val;
@Override
public String toString()
return "TreeNode" +
"val=" + val +
'';
@Override
public int compareTo(TreeNode o)
// 根据 val 值从小到大排序
return this.val - o.val;
/**
* 根据传入的数据构建一颗哈夫曼树
*
* @param array 数组
* @return 哈夫曼树根节点
*/
public TreeNode createHuffmanTree(int[] array)
if (array == null || array.length == 0)
return null;
List<TreeNode> nodeList = new ArrayList<>