《Python深度学习》第三章-2（波士顿房价-回归问题）读书笔记

Posted 2021-08-20 Paul-Huang

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了《Python深度学习》第三章-2（波士顿房价-回归问题）读书笔记相关的知识，希望对你有一定的参考价值。

第三章-2(回归问题)

本次重点：
boston_housing的回归模型(K折验证，loss=‘mse’,metrics=‘mae’)

3.1 预测房价：回归问题

回归问题
前面两个例子都是分类问题，其目标是预测输入数据点所对应的单一离散的标签。另一种常见的机器学习问题是回归问题，它预测一个连续值而不是离散的标签。

Tip：不要将回归问题与 logistic 回归算法混为一谈。令人困惑的是，logistic 回归不是回归算法，而是分类算法。
数据集介绍
- 该数据集包含美国人口普查局收集的美国马萨诸塞州波士顿住房价格的有关信息, 数据集很小，只有506个案例。数据集都有以下14个属性（具体见链接）。
- 分为 404 个训练样本和 102 个测试样本。输入数据的每个特征（比如犯罪率）都有不同的取值范围。

3.1.1 加载和准备数据

加载数据

from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

查看数据

>>> train_data.shape
(404, 13)
>>> test_data.shape
(102, 13)
>>> train_targets
array([ 15.2, 42.3, 50. ... 19.4, 19.4, 29.1])

房价大都在 10 000~50 000 美元。

准备数据
```
# 数据预处理，注意均值和方差是由训练集来的。
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std
```
注意， $\\color{red}用于测试数据标准化的均值和标准差都是在训练数据上计算得到的$ 。在工作流程中，你不能使用在测试数据上计算得到的任何结果，即使是像数据标准化这么简单的事情也不行。

3.1.2 构建网络

一般来说： $\\color{red}训练数据越少，过拟合会越严重，而较小的网络可以降低过拟合$ 。

from keras import models
from keras import layers
def build_model():
	model = models.Sequential()
	# 因为需要将同一个模型多次实例化，所以用一个函数来构建模型
	model.add(layers.Dense(64, activation='relu',
							input_shape=(train_data.shape[1],)))
	model.add(layers.Dense(64, activation='relu'))
	model.add(layers.Dense(1))
	model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
	return model

model.compile()方法用于在配置训练方法时，告知训练时用的优化器、损失函数和准确率评测标准，即：model.compile(optimizer = 优化器，loss = 损失函数， metrics = ["准确率”]) 。

本例子中:

网络的最后一层只有一个单元，没有激活，是一个线性层。这是 $\\color{red}标量回归$ （标量回归是预测单一连续值的回归）的典型设置。添加激活函数将会限制输出范围。
编译网络用的是 $\\color{red} mse 损失函数$ ，即均方误差（MSE，mean squared error），预测值与目标值之差的平方。这是回归问题常用的损失函数。
$\\color{red}平均绝对误差$ （MAE，mean absolute error）。它是预测值与目标值之差的绝对值。

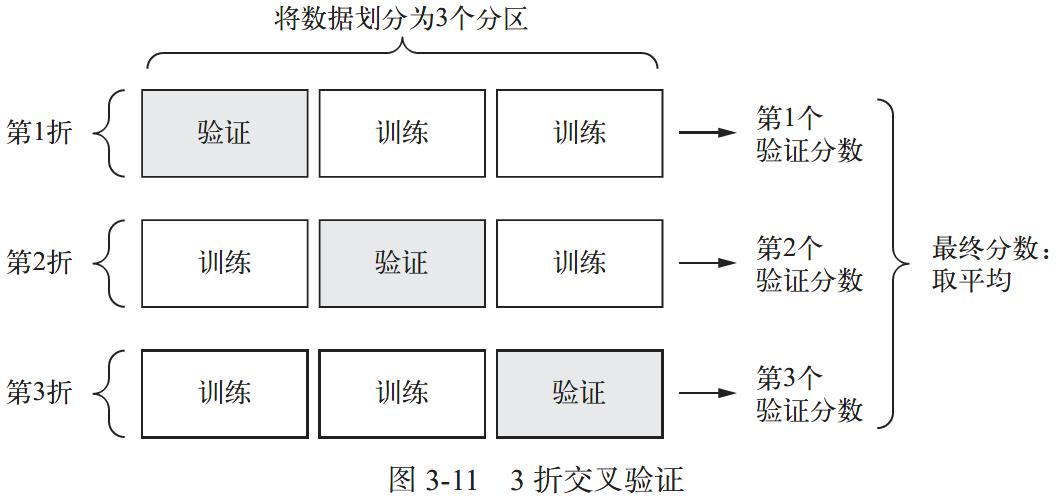
3.1.3 利用K 折验证来验证

原因
但由于 $\\color{red}数据点很少$ ，验证集会非常小（比如大约100 个样本）。 $\\color{red}验证集的划分方式$ 可能会造成验证分数上有 $\\color{red}很大的方差$ ，这样就无法对模型进行可靠的评估。
$\\color{red}K 折交叉验证$
1. 将可用数据划分为K个分区（K 通常取4 或5），实例化K个相同的模型；
2. 将每个模型在K-1 个分区上训练，并在剩下的一个分区上进行评估；
3. 模型的验证分数等于K 个验证分数的平均值。

代码实现

import numpy as np
k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []

for i in range(k):
	print('processing fold #', i)
	val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
	#准备验证数据：第k 个分区的数据
	val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
	partial_train_data = np.concatenate(
		[train_data[:i * num_val_samples],
		train_data[(i + 1) * num_val_samples:]],
		axis=0)
		# 准备训练数据：其他所有分区的数据
	partial_train_targets = np.concatenate(
		[train_targets[:i * num_val_samples],
		train_targets[(i + 1) * num_val_samples:]],
		axis=0)
	
	model = build_model()    #构建Keras 模型（已编译）
	model.fit(partial_train_data, partial_train_targets,
			epochs=num_epochs, batch_size=1, verbose=0)
	# 训练模型（静默模式，verbose=0）
	val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
	# 在验证数据上评估模型
	all_scores.append(val_mae)

fit函数的完整形式：

model.fit(训练集的输入特征，训练集的标签，batch_size= 每次喂入神经网络的样本数, 
		epochs=迭代多少次数据集, validation_data=
		(测试集的输入特征，测试集的标签，),
		 validation_split=从训练集划分多少比例给测试集，
		 validation_freq=多少次epoch测试一次)

设置num_epochs = 100，运行结果:

>>> all_scores
[1.920211911201477, 2.922642469406128, 2.498922824859619, 2.3978490829467773]
>>> np.mean(all_scores)
2.4349065721035004

每次运行模型得到的验证分数有很大差异，从1.9 到2.9 不等。平均分数（2.43）是比单一分数更可靠的指标——这就是K 折交叉验证的关键。

3.1.4 调整epochs次数并计算平均值

保存每折的验证结果

num_epochs = 500
all_mae_histories = []
for i in range(k):
	print('processing fold #', i)
	val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
	# 准备验证数据：第k 个分区的数据
	val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
	partial_train_data = np.concatenate(
		[train_data[:i * num_val_samples],
		train_data[(i + 1) * num_val_samples:]],
		axis=0) # 准备训练数据：其他所有分区的数据
	partial_train_targets = np.concatenate(
		[train_targets[:i * num_val_samples],
		train_targets[(i + 1) * num_val_samples:]],
		axis=0)
	model = build_model() #构建Keras 模型（已编译）
	history = model.fit(partial_train_data, partial_train_targets,
						validation_data=(val_data, val_targets),
						epochs=num_epochs, batch_size=1, verbose=0)
	#训练模型（静默模式，verbose=0）
	mae_history = history.history['val_mae']
	all_mae_histories.append(mae_history)

可以计算每个轮次中所有折MAE 的平均值。

计算所有轮次中的K 折验证分数平均值

average_mae_history = [
		np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

3.1.5 绘图

绘制验证分数

import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()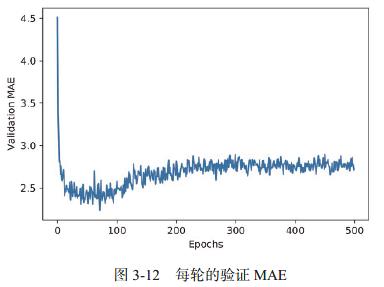

在这里插入图片描述

绘制验证分数（删除前10 个数据点）

def smooth_curve(points, factor=0.9):
	smoothed_points = []
	for point in points:
		if smoothed_points:
			previous = smoothed_points[-1]
			smoothed_points.append(previous * factor + point * (1 - factor))
		else:
			smoothed_points.append(point)
	return smoothed_points
	
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()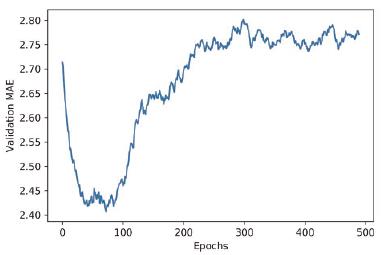

在这里插入图片描述

3.1.6 整体训练模型

model = build_model()# 一个全新的编译好的模型
model.fit(train_data, train_targets,
		epochs=80, batch_size=16, verbose=0) #在所有训练数据上训练模型
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

最终结果：

>>> test_mae_score
2.5532484335057877

相比，还是K折效果更好！

3.1.7 小结

$\\color{red}损失函数$ 。回归问题使用的损失函数与分类问题不同。回归常用的损失函数是均方误差（MSE）。
$\\color{red}回归指标$ 。同样，回归问题使用的评估指标也与分类问题不同。显而易见，精度的概念不适用于回归问题。常见的回归指标是平均绝对误差（MAE）。
$\\color{red}预处理$ 。如果输入数据的特征具有不同的取值范围，应该先进行预处理，对每个特征单独进行缩放。
$\\color{red}K折验证$ 。如果可用的数据很少，使用 K折验证可以可靠地评估模型。
$\\color{red}过拟合$ 。如果可用的训练数据很少，最好使用隐藏层较少（通常只有一到两个）的小型网络，以避免严重的过拟合。

总代码

from keras.datasets import boston_housing
from keras import models
from keras import layers
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
num_epochs = 500
all_mae_histories = []

# 数据预处理，注意均值和方差是由训练集来的。
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std

# 模型建立
def build_model():
	model = models.Sequential()
	# 因为需要将同一个模型多次实例化，所以用一个函数来构建模型
	model.add(layers.Dense(64, activation='relu',
							input_shape=(train_data.shape[1],)))
	model.add(layers.Dense(64, activation='relu'))
	model.add(layers.Dense(1))
	model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
	return model

# K折验证
for i in range(k):
	print('processing fold #', i)
	val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
	# 准备验证数据：第k 个分区的数据
	val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
	partial_train_data = np.concatenate(
		[train_data[:i * num_val_samples],
		train_data[(i + 1) * num_val_samples:]],
		axis=0) # 准备训练数据：其他所有分区的数据
	partial_train_targets = np.concatenate(
		[train_targets[:i * num_val_samples],
		train_targets[(i + 1) * num_val_samples:]],
		axis=0)
	model = build_model() #构建Keras 模型（已编译）
	history = model.fit(partial_train_data, partial_train_targets,
						validation_data=(val_data, val_targets),
						epochs=num_epochs, batch_size=1, verbose=0)
	#训练模型（静默模式，verbose=0）
	mae_history = history.history['val_mae']
	all_mae_histories.append(mae_history)

average_mae_history = [
		np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)
		]
# 绘制验证分数
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
	if smoothed_points:
		previous = smoothed_points[-1]
		smoothed_points.append(previous * factor + point * (1 - factor))
	else:
		smoothed_points.append(point)
return smoothed_points
	
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

# 整体训练模型
model = build_model()# 一个全新的编译好的模型
model.fit(train_data, train_targets,
		epochs=80, batch_size=16, verbose=0) #在所有训练数据上训练模型
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

以上是关于《Python深度学习》第三章-2（波士顿房价-回归问题）读书笔记的主要内容，如果未能解决你的问题，请参考以下文章

深度学习（波士顿房价预测）

：从线性神经网络入手深度学习（波士顿房价案例）

深度学习入门案例波士顿房价预测

机器学习之利用线性回归预测波士顿房价和可视化分析影响房价因素实战（python实现附源码超详细）

深度学习模型的构建