深度学习入门案例波士顿房价预测
Posted 川川菜鸟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习入门案例波士顿房价预测相关的知识,希望对你有一定的参考价值。
人工智能,机器学习,深度学习
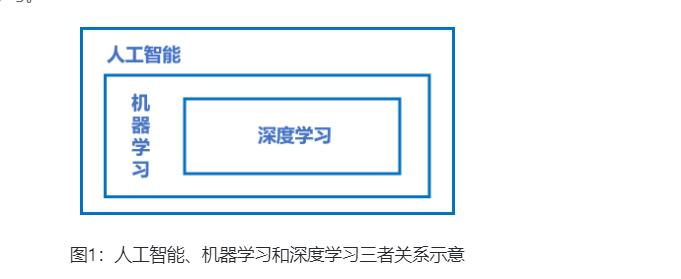
做个简单介绍:三者的关系如 图1 所示,即:人工智能 > 机器学习 > 深度学习。
深度学习设计框架:

环境查看
import paddle
import numpy as np
import os
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
print(paddle.__version__)
返回:

数据处理
在这里插入代码片
数据下载
如果你还没安装wget,点击教程安装:window配置安装wget
下载数据:
wget https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data -O housing.data
返回:

开始处理
def load_data():
# 从文件导入数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ', dtype=np.float32)
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \\
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算train数据集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \\
training_data.sum(axis=0) / training_data.shape[0]
# 记录数据的归一化参数,在预测时对数据做归一化
global max_values
global min_values
global avg_values
max_values = maximums
min_values = minimums
avg_values = avgs
# 对数据进行归一化处理
for i in range(feature_num):
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
模型设计
两步走:
定义init函数:在类的初始化函数中声明每一层网络的实现函数。在房价预测模型中,只需要定义一层全连接层,模型结构和使用Python和Numpy构建神经网络模型》章节模型保持一致。
定义forward函数:构建神经网络结构,实现前向计算过程,并返回预测结果,在本任务中返回的是房价预测结果。
class Regressor(paddle.nn.Layer):
# self代表类的实例自身
def __init__(self):
# 初始化父类中的一些参数
super(Regressor, self).__init__()
# 定义一层全连接层,输入维度是13,输出维度是1
self.fc = Linear(in_features=13, out_features=1)
# 网络的前向计算
def forward(self, inputs):
x = self.fc(inputs)
return x
训练配置
配置有如下四步:
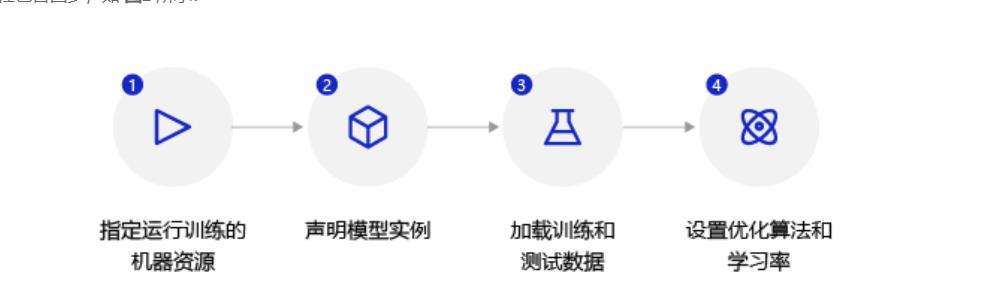
1.声明定义好的回归模型Regressor实例,并将模型的状态设置为训练。
2.使用load_data函数加载训练数据和测试数据。
3.设置优化算法和学习率,优化算法采用随机梯度下降SGD,学习率设置为0.01。
代码为:
# 声明定义好的线性回归模型
model = Regressor()
# 开启模型训练模式
model.train()
# 加载数据
training_data, test_data = load_data()
# 定义优化算法,使用随机梯度下降SGD
# 学习率设置为0.01
opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
注意:
模型实例有两种状态:训练状态.train()和预测状态.eval()。训练时要执行正向计算和反向传播梯度两个过程,而预测时只需要执行正向计算,为模型指定运行状态
训练过程
EPOCH_NUM = 10 # 设置外层循环次数
BATCH_SIZE = 10 # 设置batch大小
# 定义外层循环
for epoch_id in range(EPOCH_NUM):
# 在每轮迭代开始之前,将训练数据的顺序随机的打乱
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个batch包含10条数据
mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
# 定义内层循环
for iter_id, mini_batch in enumerate(mini_batches):
x = np.array(mini_batch[:, :-1]) # 获得当前批次训练数据
y = np.array(mini_batch[:, -1:]) # 获得当前批次训练标签(真实房价)
# 将numpy数据转为飞桨动态图tensor形式
house_features = paddle.to_tensor(x)
prices = paddle.to_tensor(y)
# 前向计算
predicts = model(house_features)
# 计算损失
loss = F.square_error_cost(predicts, label=prices)
avg_loss = paddle.mean(loss)
if iter_id%20==0:
print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.numpy()))
# 反向传播
avg_loss.backward()
# 最小化loss,更新参数
opt.step()
# 清除梯度
opt.clear_grad()
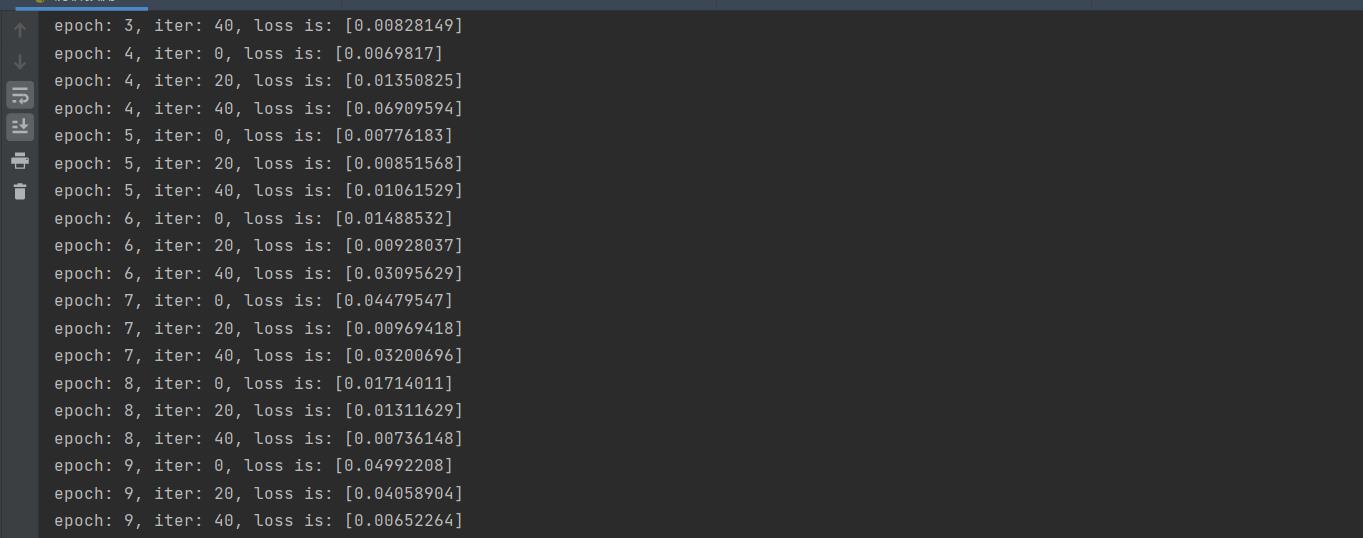
返回:
保存模型
将模型当前的参数数据model.state_dict()保存到文件中(通过参数指定保存的文件名 LR_model),以备预测或校验的程序调用。
代码为:
# 保存模型参数,文件名为LR_model.pdparams
paddle.save(model.state_dict(), 'LR_model.pdparams')
print("模型保存成功,模型参数保存在LR_model.pdparams中")
测试模型
通过load_one_example函数实现从数据集中抽一条样本作为测试样本,具体实现代码如下所示。
def load_one_example():
# 从上边已加载的测试集中,随机选择一条作为测试数据
idx = np.random.randint(0, test_data.shape[0])
idx = -10
one_data, label = test_data[idx, :-1], test_data[idx, -1]
# 修改该条数据shape为[1,13]
one_data = one_data.reshape([1,-1])
return one_data, label
# 参数为保存模型参数的文件地址
model_dict = paddle.load('LR_model.pdparams')
model.load_dict(model_dict)
model.eval()
# 参数为数据集的文件地址
one_data, label = load_one_example()
# 将数据转为动态图的variable格式
one_data = paddle.to_tensor(one_data)
predict = model(one_data)
# 对结果做反归一化处理
predict = predict * (max_values[-1] - min_values[-1]) + avg_values[-1]
# 对label数据做反归一化处理
label = label * (max_values[-1] - min_values[-1]) + avg_values[-1]
print("Inference result is {}, the corresponding label is {}".format(predict.numpy(), label))
返回:

通过比较“模型预测值”和“真实房价”可见,模型的预测效果与真实房价接近。
参考资料
百度深度学习飞桨:
https://www.paddlepaddle.org.cn/
完整源码
# coding=gbk
"""
作者:川川
@时间 : 2021/8/29 15:40
群:970353786
"""
#加载飞桨、Numpy和相关类库
import paddle
from paddle.nn import Linear
import paddle.nn.functional as F
import numpy as np
def load_data():
# 从文件导入数据
datafile = './housing.data'
data = np.fromfile(datafile, sep=' ', dtype=np.float32)
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \\
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算train数据集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \\
training_data.sum(axis=0) / training_data.shape[0]
# 记录数据的归一化参数,在预测时对数据做归一化
global max_values
global min_values
global avg_values
max_values = maximums
min_values = minimums
avg_values = avgs
# 对数据进行归一化处理
for i in range(feature_num):
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
class Regressor(paddle.nn.Layer):
# self代表类的实例自身
def __init__(self):
# 初始化父类中的一些参数
super(Regressor, self).__init__()
# 定义一层全连接层,输入维度是13,输出维度是1
self.fc = Linear(in_features=13, out_features=1)
# 网络的前向计算
def forward(self, inputs):
x = self.fc(inputs)
return x
# 声明定义好的线性回归模型
model = Regressor()
# 开启模型训练模式
model.train()
# 加载数据
training_data, test_data = load_data()
# 定义优化算法,使用随机梯度下降SGD
# 学习率设置为0.01
opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
EPOCH_NUM = 10 # 设置外层循环次数
BATCH_SIZE = 10 # 设置batch大小
# 定义外层循环
for epoch_id in range(EPOCH_NUM):
# 在每轮迭代开始之前,将训练数据的顺序随机的打乱
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个batch包含10条数据
mini_batches = [training_data[k:k + BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
# 定义内层循环
for iter_id, mini_batch in enumerate(mini_batches):
x = np.array(mini_batch[:, :-1]) # 获得当前批次训练数据
y = np.array(mini_batch[:, -1:]) # 获得当前批次训练标签(真实房价)
# 将numpy数据转为飞桨动态图tensor形式
house_features = paddle.to_tensor(x)
prices = paddle.to_tensor(y)
# 前向计算
predicts = model(house_features)
# 计算损失
loss = F.square_error_cost(predicts, label=prices)
avg_loss = paddle.mean(loss)
if iter_id % 20 == 0:
print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.numpy()))
# 反向传播
avg_loss.backward()
# 最小化loss,更新参数
opt.step()
# 清除梯度
opt.clear_grad()
# 保存模型
# 保存模型参数,文件名为LR_model.pdparams
paddle.save(model.state_dict(), 'LR_model.pdparams')
print("模型保存成功,模型参数保存在LR_model.pdparams中")
##测试模型
def load_one_example():
# 从上边已加载的测试集中,随机选择一条作为测试数据
idx = np.random.randint(0, test_data.shape[0])
idx = -10
one_data, label = test_data[idx, :-1], test_data[idx, -1]
# 修改该条数据shape为[1,13]
one_data = one_data.reshape([1,-1])
return one_data, label
# 参数为保存模型参数的文件地址
model_dict = paddle.load('LR_model.pdparams')
model.load_dict(model_dict)
model.eval()
# 参数为数据集的文件地址
one_data, label = load_one_example()
# 将数据转为动态图的variable格式
one_data = paddle.to_tensor(one_data)
predict = model(one_data)
# 对结果做反归一化处理
predict = predict * (max_values[-1] - min_values[-1]) + avg_values[-1]
# 对label数据做反归一化处理
label = label * (max_values[-1] - min_values[-1]) + avg_values[-1]
print("Inference result is {}, the corresponding label is {}".format(predict.numpy(), label))
希望能帮到你))
以上是关于深度学习入门案例波士顿房价预测的主要内容,如果未能解决你的问题,请参考以下文章