BP神经网络原理（详细推导）

Posted 2021-08-20 Sun-sky

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了BP神经网络原理（详细推导）相关的知识，希望对你有一定的参考价值。

文章目录

前言
第一步：正向传播激活神经网络
第二步：误差逆向传播
总结

前言

BP神经网络（Back propagation neural network）全称为多层前馈神经网络，其用于解决非线性问题。整个神经网络的步骤为：输入层接收外界的输入，隐藏层和输出层的神经元对输入的特征或信号通过权重矩阵进行加工，最终输出结果。过程中最重要的是获得加工所要的权重，本质上说神经网络的学习过程就是在学习神经元与神经元之间连接的权重。

提示：以下是本篇文章正文内容，下面案例可供参考

第一步：正向传播激活神经网络

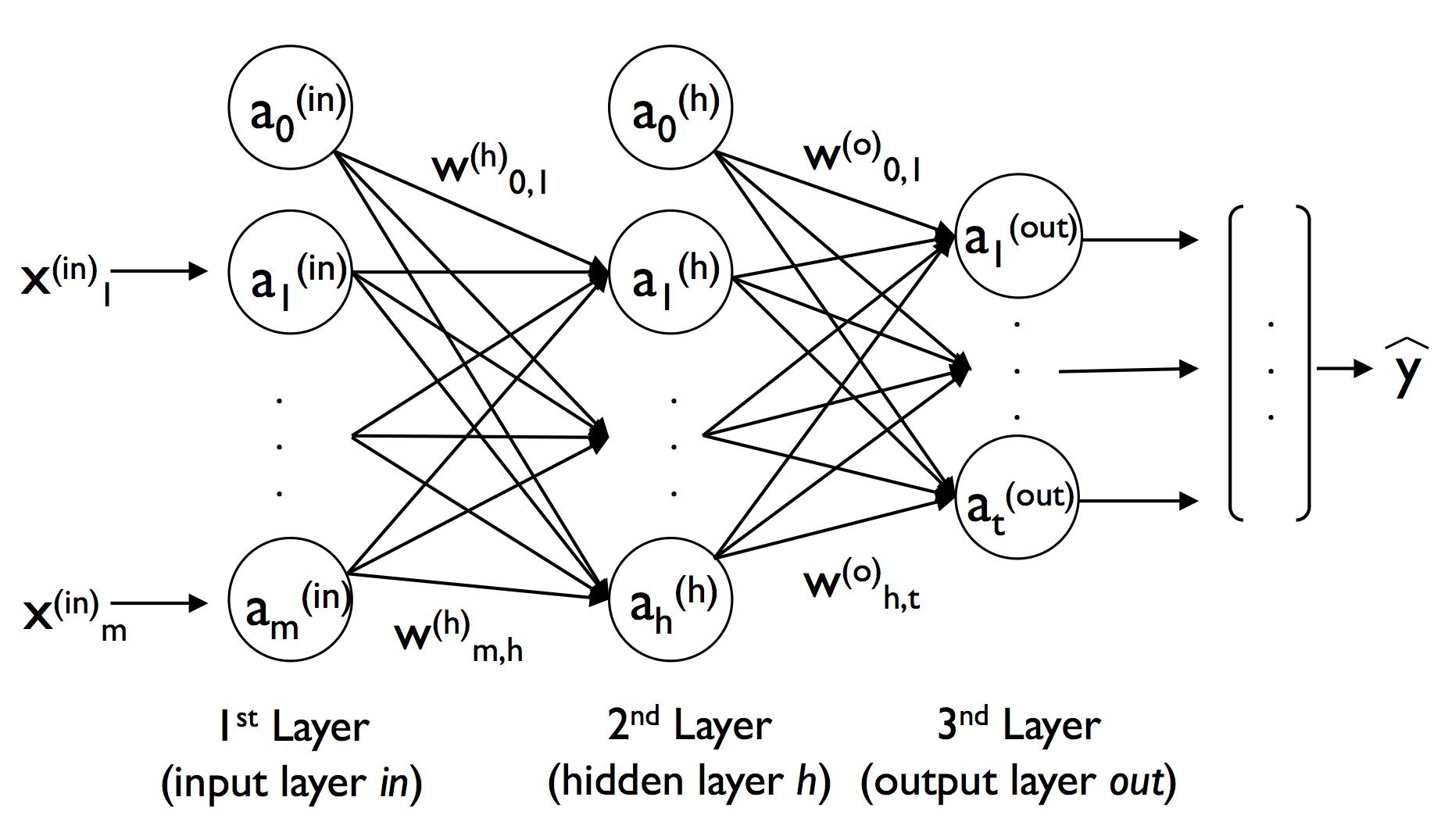
A.变量说明

关于BP神经网络的正向传播，我们以上图为例对变量进行一下说明：

$x^{(in)}_i ，a^{(in)}_i$ : 二者均表示输入层的第 $i$ 个输入单元（这样做是为了和后面的进行统一，二者相等的原因是输入层的神经元不起激活作用）；
$w^{(h)}_{m,h}$ :输入层的第 $m$ 个单元与隐藏层的的第 $h$ 个单元之间的权重（⚠️权重的标识很重要，而且不同的参考书用的也不同，读者一定要弄清楚）
$z^{(h)}_i$ : 隐藏层的第 $i$ 的净输入单元， $z^{(h)}_i =w^{(h)}_{1,i}a^{(in)}_1+ ...+w^{(h)}_{m,i}a^{(in)}_m$ ；
$a^{(h)}_i$ : 隐藏层的第 $i$ 的隐藏单元， $a^{(h)}_i = \\phi (z^{(h)}_i)$ ；
$w^{(o)}_{h,t}$ :隐藏层的第 $h$ 个单元与输出层的的第 $t$ 个单元之间的权重（⚠️权重的标识很重要，而且不同的参考书用的也不同，读者一定要弄清楚）
$z^{(out)}_i$ : 输出层的第 $i$ 的净输入单元， $z^{(out)}_i =w^{(out)}_{1,i}a^{(h)}_1+ ...+w^{(out)}_{h,i}a^{(h)}_h$ ；
$a^{(out)}_i$ : 输出层的第 $i$ 的输出单元， $a^{(out)}_i = \\phi (z^{(out)}_i)$ ；
$y^{[i]},a^{[i]}$ : 分别代表一组数据的实际结果中的第 $i$ 个（上角标视为索引），经过神经网络输出的第 $i$ 个；
关于激活函数，我们采用 sigmoid 函数 $\\phi (x) = \\cfrac{1}{1 + e^{-x}}$ ;

B.正向传播

熟悉完上面的量的意义之后，我们通过线性代数的知识导出BP神经网络的正向传播过程：

首先，输入层的各个单元 $\\bm A^{(in)}$ (不妨设阶数为：n*m )和通过指向隐藏层的权重矩阵 $\\bm W^{(h)}$ （阶数：m * h）做点乘，得到隐藏层的净输入向量： $\\bm Z^{(h)}$ （阶数： n * h）；

其次，将隐藏层的净输入向量进行激活，得到 $\\bm A^{(h)}$ ， $\\bm A^{(h)} = \\phi（\\bm Z^{(h)}）$ （阶数：n * h）；

再其次： $\\bm a^{(h)}$ 通过指向输出层的权重矩阵 $\\bm W^{(out)}$ （阶数：h * t），得到输出层的净输入向量： $\\bm Z^{(out)}$ （n * t）；

最后，将输出层的净输入向量进行激活，得到得到 $\\bm A^{(out)}$ ， $\\bm A^{(out)} = \\phi（\\bm Z^{(out}）$ （阶数：n * t），即我们的输出结果。

这其中涉及的矩阵运算罗列如下：

$\\bm Z^{(h)} = \\bm A^{(in)}\\bm W^{(h)}$ ;