BP算法的原理解释和推导
Posted Super__Tiger
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BP算法的原理解释和推导相关的知识,希望对你有一定的参考价值。
BP算法的原理解释和推导
已知的神经网络结构:

且已知的条件:
- a ( j ) = f ( z ( j ) ) \\mathbfa^\\left( \\mathbfj \\right)=\\mathbff\\left( \\mathbfz^\\left( \\mathbfj \\right) \\right) a(j)=f(z(j))
- z ( j ) = W ( j ) a ( j − 1 ) + b ( j ) ,而 θ ( j ) = W ( j ) , b ( j ) \\mathbfz^\\left( \\mathbfj \\right)=\\mathbfW^\\left( \\mathbfj \\right)\\mathbfa^\\left( \\mathbfj-1 \\right)+\\mathbfb^\\left( \\mathbfj \\right)\\text,而\\mathbf\\theta ^\\left( \\mathbfj \\right)=\\left\\ \\mathbfW^\\left( \\mathbfj \\right),\\mathbfb^\\left( \\mathbfj \\right) \\right\\ z(j)=W(j)a(j−1)+b(j),而θ(j)=W(j),b(j)
对于上图,如果我们想得到 ∂ l ∂ θ ( j ) \\frac\\partial \\mathbfl\\partial \\mathbf\\theta ^\\left( \\mathbfj \\right) ∂θ(j)∂l,可以通过 z ( j ) \\mathbfz^\\left( \\mathbfj \\right) z(j)建立l和θ(j)之间的联系,即 ∂ l ∂ θ ( j ) = ∂ l ∂ z ( j ) ∗ ∂ z ( j ) ∂ θ ( j ) \\frac\\partial \\mathbfl\\partial \\mathbf\\theta ^\\left( \\mathbfj \\right)=\\frac\\partial \\mathbfl\\partial \\mathbfz^\\left( \\mathbfj \\right)*\\frac\\partial \\mathbfz^\\left( \\mathbfj \\right)\\partial \\mathbf\\theta ^\\left( \\mathbfj \\right) ∂θ(j)∂l=∂z(j)∂l∗∂θ(j)∂z(j),而l和z(j)之间的联系则可以通过z(j+1)进行建立 ∂ l ∂ z ( j ) = ∂ l ∂ z ( j + 1 ) ∗ ∂ z ( j + 1 ) ∂ z ( j ) = ∂ l ∂ z ( j + 1 ) ∗ ∂ z ( j + 1 ) ∂ a ( j ) ∗ ∂ a ( j ) ∂ z ( j ) \\frac\\partial \\mathbfl\\partial \\mathbfz^\\left( \\mathbfj \\right)=\\frac\\partial \\mathbfl\\partial \\mathbfz^\\left( \\mathbfj+1 \\right)*\\frac\\partial \\mathbfz^\\left( \\mathbfj+1 \\right)\\partial \\mathbfz^\\left( \\mathbfj \\right)=\\frac\\partial \\mathbfl\\partial \\mathbfz^\\left( \\mathbfj+1 \\right)*\\frac\\partial \\mathbfz^\\left( \\mathbfj+1 \\right)\\partial \\mathbfa^\\left( \\mathbfj \\right)*\\frac\\partial \\mathbfa^\\left( \\mathbfj \\right)\\partial \\mathbfz^\\left( \\mathbfj \\right) ∂z(j)∂l=∂z(j+1)∂l∗∂z(j)∂z(j+1)=∂z(j+1)∂l∗∂a(j)∂z(j+1)∗∂z(j)∂a(j),由此,我们得到 ∂ l ∂ θ ( j ) = ∂ l ∂ z ( j + 1 ) ∗ ∂ z ( j + 1 ) ∂ a ( j ) ∗ ∂ a ( j ) ∂ z ( j ) ∗ ∂ z ( j ) ∂ θ ( j ) \\frac\\partial \\mathbfl\\partial \\mathbf\\theta ^\\left( \\mathbfj \\right)=\\frac\\partial \\mathbfl\\partial \\mathbfz^\\left( \\mathbfj+1 \\right)*\\frac\\partial \\mathbfz^\\left( \\mathbfj+1 \\right)\\partial \\mathbfa^\\left( \\mathbfj \\right)*\\frac\\partial \\mathbfa^\\left( \\mathbfj \\right)\\partial \\mathbfz^\\left( \\mathbfj \\right)*\\frac\\partial \\mathbfz^\\left( \\mathbfj \\right)\\partial \\mathbf\\theta ^\\left( \\mathbfj \\right) ∂θ(j)∂l=∂z(j+1)∂l∗∂a(j)∂z(j+1)∗∂z(j)∂a(j)∗∂θ(j)∂z(j)(链式求导法则),然后不断的迭代求导下去。
这里我们细心观察下式:
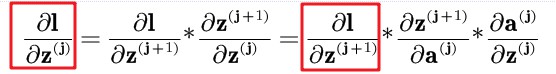
其中, ∂ z ( j + 1 ) ∂ a ( j ) = w ( j + 1 ) \\frac\\partial \\mathbfz^\\left( \\mathbfj+1 \\right)\\partial \\mathbfa^\\left( \\mathbfj \\right)=\\mathbfw^\\left( \\mathbfj+1 \\right) ∂a(j)∂z(j+1)=w以上是关于BP算法的原理解释和推导的主要内容,如果未能解决你的问题,请参考以下文章