BP神经网络算法推导

Posted 2023-02-22 伤心兮

一、BP神经网络

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛也是最简单的神经网络模型之一。

1.1 BP神经网络的结构

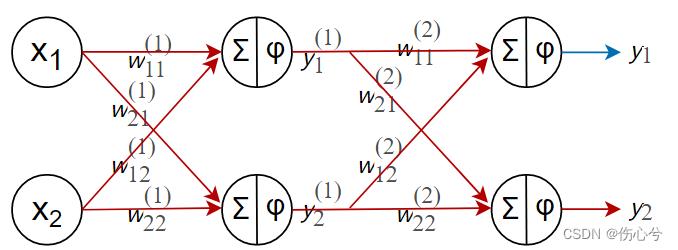
• 神经网络结构如下
• 其中$x_1,x_2$为输入，$\phi$为激活函数。BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。其均方误差表达式为$$\begin{array}{r}F=e_1^2+e_2^2=(d_1-y_1{)}^2+(d_2-y_2{)}^2\end{array}$$其中$e_1,e_2$为误差，$d_1,d_2$为样本真实标签，$y_1,y_2$为预测输。

1.2 BP神经网络算法流程

• BP神经网络包括前向传播的反向传播，其算法流程图如图所示，
  首先给定算法模型的输入输出，也就是所说的训练集。接着求取模型的实际输出，就是模型计算输出的真实值。之后进行误差的计算，当误差满足所设需求时，一般为90%-95%，或者循环次数达到所设置值时，则结束训练。否则求取误差梯度和权值阈值更新，重复求取实际输出。

1.3 前向传播

输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。以$y_1$这一条线路为例，
其前向传播公式为$$\begin{array}{r}{y}_1^{(1)}=\phi (x_1\cdot w_{11}^{(1)}+x_2\cdot w_{12}^{(1)})\end{array}$$令$v_1^{(1)}=x_1\cdot w_{11}^{(1)}+x_2\cdot w_{12}^1$,则上式变为
$$\begin{array}{r}{y}_1^{(1)}=\phi (v_1^{(1)})\end{array}$$最终前向传播的结果为$$\begin{array}{r}{y}_1=\phi (y_1^{(1)}\cdot w_{11}^{(2)}+y_2^{(1)}\cdot w_{12}^{(2)})\end{array}$$最终误差为：$$\begin{array}{r}{e}_1^2=[d_1-\phi (y_1^{(1)}\cdot w_{11}^{(2)}+y_2^{(1)}\cdot w_{12}^{(2)}){]}^2\end{array}$$令$v_1^{(2)}=y_1^{(1)}\cdot w_{11}^{(2)}+y_2^{(1)}\cdot w_{12}^{(2)}$得到， e 1 2 = [ d 1 − φ ( v 1 ( 2 ) ) ] 2 \\beginalign e_1^2=[d_1-\\varphi(v_1^(2))]^2 \\endalign BP神经网络算法推导

BP算法基本原理推导----《机器学习》笔记

神经网络——BP学习算法：反向传播算法推导

神经网络 误差逆传播算法推导 BP算法

卷积神经网络 CNN BP算法推导

神经网络——BP学习算法推导