Opencv3中SURF算法学习
Posted lucifer_zhy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Opencv3中SURF算法学习相关的知识,希望对你有一定的参考价值。
目录
流程图:
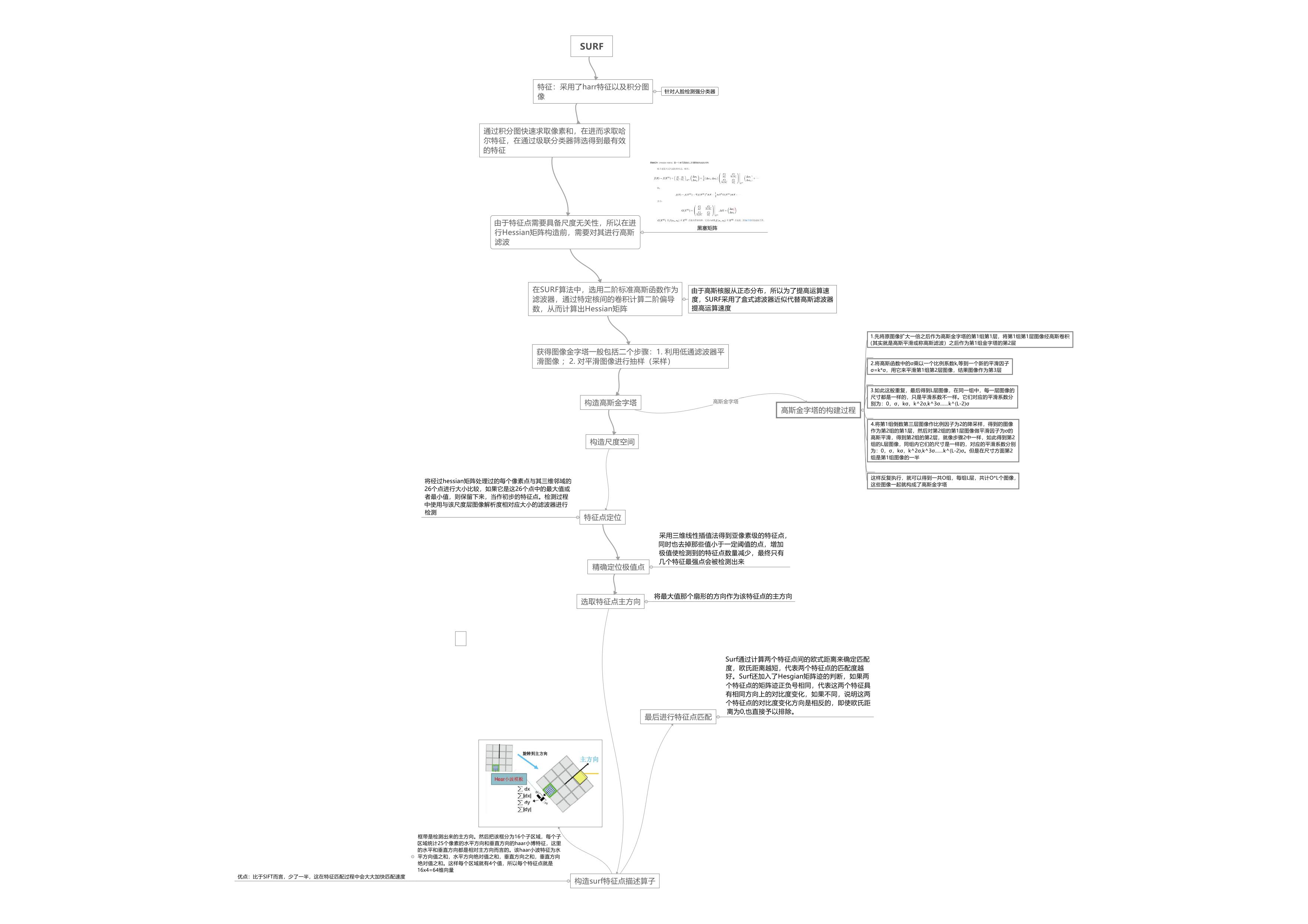
下载链接:https://download.csdn.net/download/qq_46418503/20416054
SURF算法:SURF(加速版的具有鲁棒性的特征),SURF是尺度不变特征变换算法(SIFT算法)的加速版。SURF最大的特征在于采用了harr特征以及积分图像的概念。
哈尔特征harr
Haar(哈尔)特征分为三类:边缘特征、线性特征、中心特征和对角线特征,组合成特征模板。特征模板内有白色和黑色两种矩形,并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。Haar特征值反映了图像的灰度变化情况。例如:脸部的一些特征能由矩形特征简单的描述,如:眼睛要比脸颊颜色要深,鼻梁两侧比鼻梁颜色要深,嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构,如边缘、线段较敏感,所以只能描述特定走向(水平、垂直、对角)的结构。

对于图中的A, B和D这类特征,特征数值计算公式为:v=Σ白-Σ黑,而对于C来说,计算公式如下:v=Σ白-2*Σ黑;之所以将黑色区域像素和乘以2,是为了使两种矩形区域中像素数目一致。我们希望当把矩形放到人脸区域计算出来的特征值和放到非人脸区域计算出来的特征值差别越大越好,这样就可以用来区分人脸和非人脸。
通过改变特征模板的大小和位置,可在图像子窗口中穷举出大量的特征。上图的特征模板称为“特征原型”;特征原型在图像子窗口中扩展(平移伸缩)得到的特征称为“矩形特征”;矩形特征的值称为“特征值”。
常用的矩形特征有三种:两矩形特征、三矩形特征、四矩形特征,如图:
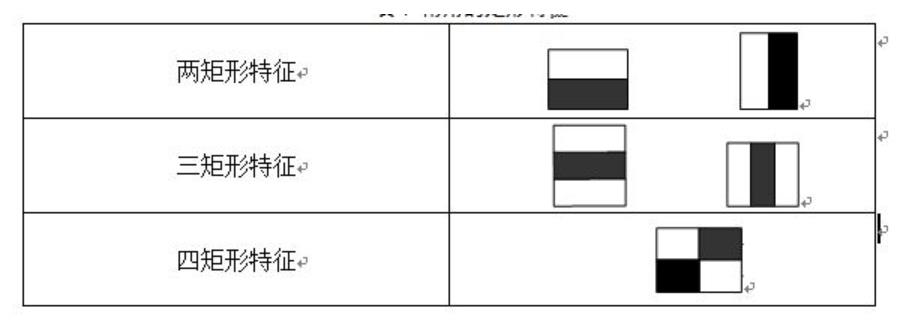
由图表可以看出,两矩形特征反映的是边缘特征,三矩形特征反映的是线性特征、四矩形特征反映的是特定方向特征。

上图中两个矩形特征,表示出人脸的某些特征。比如中间一幅表示眼睛区域的颜色比脸颊区域的颜色深,右边一幅表示鼻梁两侧比鼻梁的颜色要深。同样,其他目标,如眼睛等,也可以用一些矩形特征来表示。使用特征比单纯地使用像素点具有很大的优越性,并且速度更快。
子窗口中的特征个数即为特征矩形的个数。训练时,将每一个特征在训练图像子窗口中进行滑动计算,获取各个位置的各类矩形特征。在子窗口中位于不同位置的同一类型矩形特征,属于不同的特征。可以证明,在确定了特征的形式之后,矩形特征的数量只与子窗口的大小有关。在24×24的检测窗口中,矩形特征的数量约为160,000个。特征模板可以在子窗口内以“任意”尺寸“任意”放置,每一种形态称为一个特征。找出子窗口所有特征,是进行弱分类训练的基础。
子窗口内的条件矩形,矩形特征个数的计算:
如图所示的一个m*m大小的子窗口,可以计算在这么大的子窗口内存在多少个矩形特征。
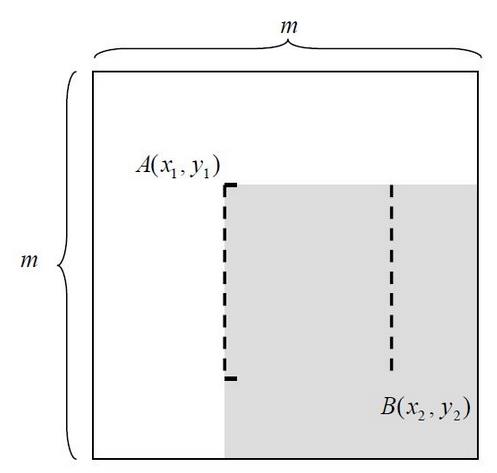
以 m×m 像素分辨率的检测器为例,其内部存在的满足特定条件的所有矩形的总数可以这样计算:
对于 m×m 子窗口,我们只需要确定了矩形左上顶点A(x1,y1)和右下顶点B(x2,63) ,即可以确定一个矩形;如果这个矩形还必须满足下面两个条件(称为(s, t)条件,满足(s, t)条件的矩形称为条件矩形):
1) x 方向边长必须能被自然数s 整除(能均等分成s 段);
2) y 方向边长必须能被自然数t 整除(能均等分成t 段);
于是这个矩形的最小尺寸为s×t 或t×s, 最大尺寸为[m/s]·s×[m/t]·t 或[m/t]·t×[m/s]·s;其中[ ]为取整运算符。//此处没有太懂,有懂兄台的希望可以留言告诉我下是什么意思;个人理解的s是分出来的最小矩形的其一边长为s,而不是分为s段;

由上分析可知,在m×m 子窗口中,满足(s, t)条件的所有矩形的数量为:
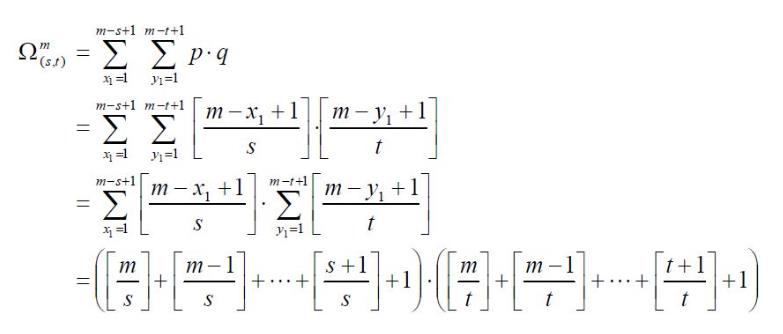
实际上,(s, t)条件描述了矩形特征的特征,下面列出了不同矩形特征对应的(s, t)条件:

下面以 24×24 子窗口为例,具体计算其特征总数量:

下面列出了,在不同子窗口大小内,特征的总数量:

矩形特征可位于图像任意位置,大小也可以任意改变,所以矩形特征值是矩形模版类别、矩形位置和矩形大小这三个因素的函数。故类别、大小和位置的变化,使得很小的检测窗口含有非常多的矩形特征,如:在24*24像素大小的检测窗口内矩形特征数量可以达到16万个。这样就有两个问题需要解决了:
(1)如何快速计算那么多的特征?---积分图大显神通;
(2)哪些矩形特征才是对分类器分类最有效的?---如通过AdaBoost算法来训练。
积分图
积分图就是只遍历一次图像就可以求出图像中所有区域像素和的快速算法,大大的提高了图像特征值计算的效率。
积分图主要的思想是将图像从起点开始到各个点所形成的矩形区域像素之和作为一个数组的元素保存在内存中,当要计算某个区域的像素和时可以直接索引数组的元素,不用重新计算这个区域的像素和,从而加快了计算(这有个相应的称呼,叫做动态规划算法)。积分图能够在多种尺度下,使用相同的时间(常数时间)来计算不同的特征,因此大大提高了检测速度。
积分图是一种能够描述全局信息的矩阵表示方法。积分图的构造方式是,位置(A)处的值是原图像在位置(A)左上角方向所有像素的和;
而Haar-like特征值无非就是两个矩阵像素和的差,同样可以在常数时间内完成。
一个区域的像素值的和,可以由该区域的端点的积分图来计算。由前面特征模板的特征值的定义可以推出,矩形特征的特征值可以由特征端点的积分图计算出来。以A矩形特征为例,如下图,使用积分图计算其特征值:
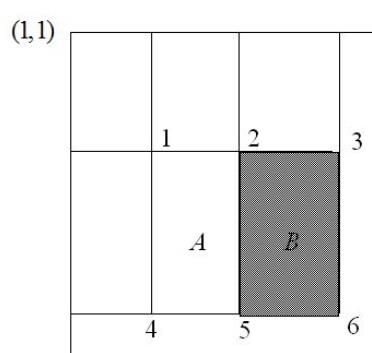
该矩形特征的特征值,由定义,为区域A的像素值减去区域B的像素值。
区域A的像素值:ii(5)+ii(1)-ii(2)-ii(4) ········(a)
区域B的像素值:ii(6)+ii(2)-ii(5)-ii(3) ········(b)
所以:该矩形特征的特征值(a)-(b);
所以,矩形特征的特征值,只与特征矩形的端点的积分图有关,而与图像的坐标无关。通过计算特征矩形的端点的积分图,再进行简单的加减运算,就可以得到特征值,正因为如此,特征的计算速度大大提高,也提高了目标的检测速度。
AdaBoost级联分类器
级联分类模型是树状结构可以用下图表示:
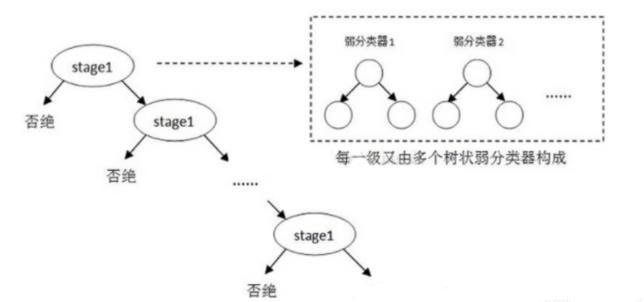
其中每一个stage都代表一级强分类器。当检测窗口通过所有的强分类器时才被认为是正样本,否则拒绝。实际上,不仅强分类器是树状结构,强分类器中的每一个弱分类器也是树状结构。由于每一个强分类器对负样本的判别准确度非常高,所以一旦发现检测到的目标位负样本,就不在继续调用下面的强分类器,减少了很多的检测时间。因为一幅图像中待检测的区域很多都是负样本,这样由级联分类器在分类器的初期就抛弃了很多负样本的复杂检测,所以级联分类器的速度是非常快的;只有正样本才会送到下一个强分类器进行再次检验,这样就保证了最后输出的正样本的伪正(false positive)的可能性非常低。
级联分类器是如何训练的呢?首先需要训练出每一个弱分类器,然后把每个弱分类器按照一定的组合策略,得到一个强分类器,我们训练出多个强分类器,然后按照级联的方式把它们组合在一块,就会得到我们最终想要的Haar分类器。
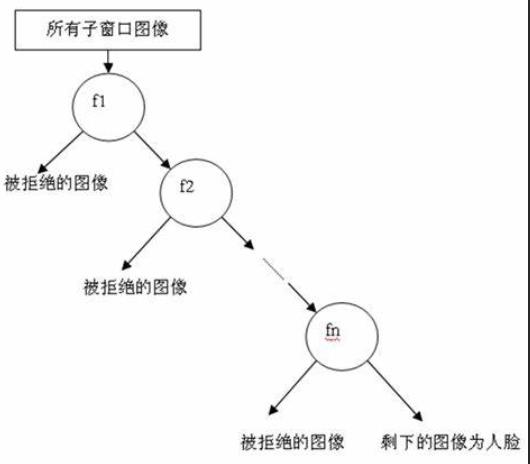
一个弱分类器就是一个基本和上图类似的决策树,最基本的弱分类器只包含一个Haar-like特征,也就是它的决策树只有一层,被称为树桩(stump)。
以20*20图像为例,78,460个特征,如果直接利用AdaBoost训练,那么工作量是极其极其巨大的。
所以必须有个筛选的过程,筛选出T个优秀的特征值(即最优弱分类器),然后把这个T个最优弱分类器传给AdaBoost进行训练。
弱分类器训练:
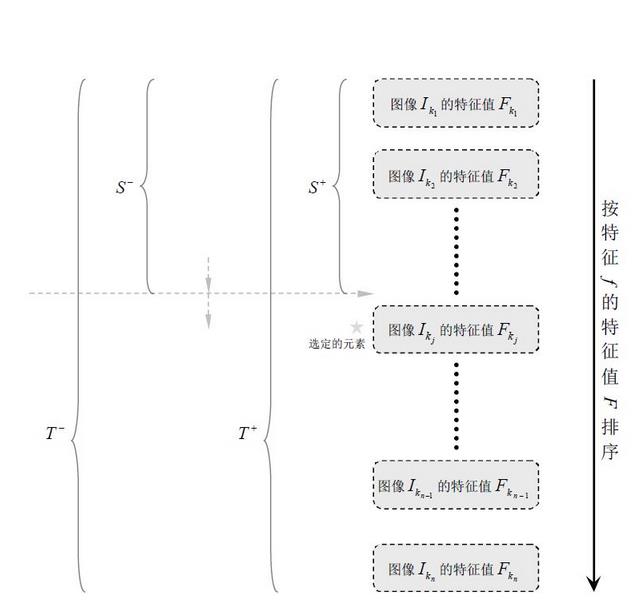
1、对于每个特征 ,计算所有训练样本的特征值,并将其排序:
2、扫描一遍排好序的特征值,对排好序的表中的每个元素,计算下面四个值:
计算全部正例的权重和 ;
计算全部负例的权重和 ;
计算该元素前之前的正例的权重和 ;
计算该元素前之前的负例的权重和 ;
3、选取当前元素的特征值 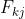 和它前面的一个特征值Fk,j−1之间的数作为阈值,所得到的弱分类器就在当前元素处把样本分开 —— 也就是说这个阈值对应的弱分类器将当前元素前的所有元素分为人脸(或非人脸),而把当前元素后(含)的所有元素分为非人脸(或人脸)。该阈值的分类误差为:
和它前面的一个特征值Fk,j−1之间的数作为阈值,所得到的弱分类器就在当前元素处把样本分开 —— 也就是说这个阈值对应的弱分类器将当前元素前的所有元素分为人脸(或非人脸),而把当前元素后(含)的所有元素分为非人脸(或人脸)。该阈值的分类误差为:
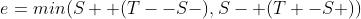
于是,通过把这个排序表从头到尾扫描一遍就可以为弱分类器选择使分类误差最小的阈值(最优阈值),也就是选取了一个最佳弱分类器。
强分类器训练:

注意,这里所说的T=200个弱分类器,指的是非级联的强分类器。若果是用级联的强分类器,则每个强分类器的弱分类器的个数会相对较少。
一般学术界所说的级联分类器,都是指的是级联强分类器,一般情况有10个左右的强分类器,每个强分类有10-20个弱分类器。当然每一层的强分类器中弱分类器的个数可以不相等,可以根据需要在前面的层少放一些弱分类器,后面的层次逐渐的增加弱分类器的个数。
SURF原理
(1)构建Hessian矩阵构造高斯金字塔尺度空间
黑塞矩阵
黑塞矩阵(Hessian Matrix)是一个多元函数的二阶偏导数构成的方阵;

SIFT采用的是DoG图像,而SURF采用的是Hessian矩阵(SURF算法核心)行列式近似值图像。在数学中,Hessian矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,即每一个像素点都可以求出一个2x2的Hessian矩阵,可计算出其行列式detH,可以利用行列式取值正负来判别该点是或不是极值点来将所有点分类。在SURF算法中,选用二阶标准高斯函数作为滤波器,通过特定核间的卷积计算二阶偏导数,从而计算出Hessian矩阵,但是由于特征点需要具备尺度无关性,所以在进行Hessian矩阵构造前,需要对其进行高斯滤波(由于高斯核服从正态分布,所以为了提高运算速度,SURF采用了盒式滤波器近似代替高斯滤波器提高运算速度),即与以方差为自变量的高斯函数的二阶导数进行卷积。通过这种方法可以为图像中每个像素计算出其H的行列式的决定值,并用这个值来判别特征点。
图像金字塔
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。
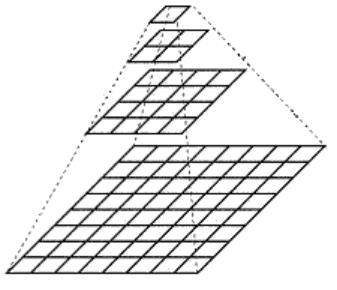
获得图像金字塔一般包括二个步骤:1. 利用低通滤波器平滑图像 ;2. 对平滑图像进行抽样(采样)。有两种采样方式——上采样(分辨率逐级升高)和下采样(分辨率逐级降低)
高斯金字塔
高斯金字塔式在Sift算子中提出来的概念,首先高斯金字塔并不是一个金字塔,而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval)。
高斯金字塔构建过程:
1. 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第2层,高斯卷积函数为:
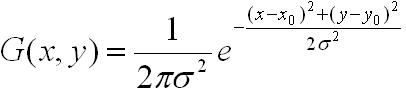
对于参数σ,在Sift算子中取的是固定值1.6。
2. 将σ乘以一个比例系数k,等到一个新的平滑因子σ=k*σ,用它来平滑第1组第2层图像,结果图像作为第3层。
3. 如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。它们对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。
4. 将第1组倒数第三层图像作比例因子为2的降采样,得到的图像作为第2组的第1层,然后对第2组的第1层图像做平滑因子为σ的高斯平滑,得到第2组的第2层,就像步骤2中一样,如此得到第2组的L层图像,同组内它们的尺寸是一样的,对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。但是在尺寸方面第2组是第1组图像的一半。
这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起就构成了高斯金字塔,结构如下:
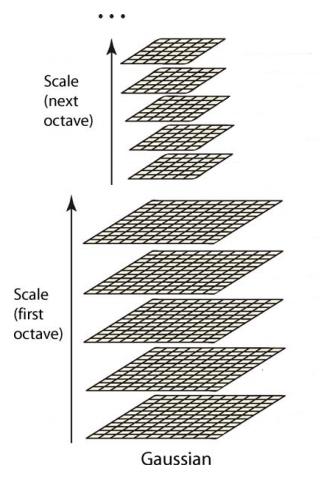
在同一组内,不同层图像的尺寸是一样的,后一层图像的高斯平滑因子σ是前一层图像平滑因子的k倍;在不同组内,后一组第一个图像是前一组倒数第三个图像的二分之一采样,图像大小是前一组的一半;
DOG金字塔
差分金字塔,DOG(Difference of Gaussian)金字塔是在高斯金字塔的基础上构建起来的,其实生成高斯金字塔的目的就是为了构建DOG金字塔。
DOG金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。概括为DOG金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。
DOG金字塔的构建可以用下图描述:
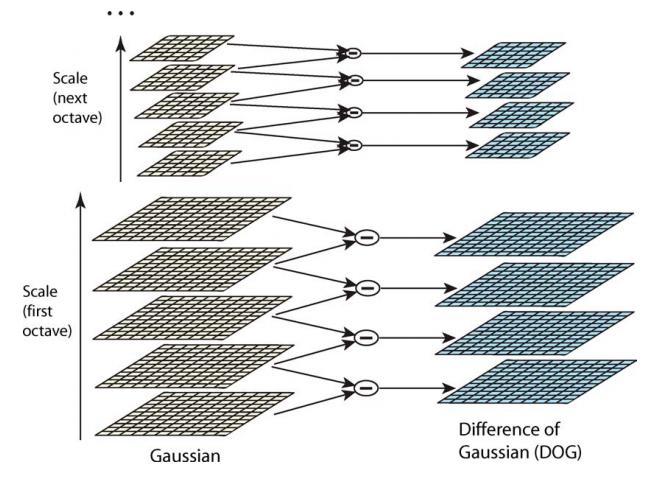
每一组在层数上,DOG金字塔比高斯金字塔少一层。后续Sift特征点的提取都是在DOG金字塔上进行的。
尺度空间
图像的尺度空间解决的问题是如何对图像在所有尺度下描述的问题。在高斯金字塔中一共生成O组L层不同尺度的图像,这两个量合起来(O,L)就构成了高斯金字塔的尺度空间,也就是说以高斯金字塔的组O作为二维坐标系的一个坐标,不同层L作为另一个坐标,则给定的一组坐标(O,L)就可以唯一确定高斯金字塔中的一幅图像。
尺度空间的形象表述:
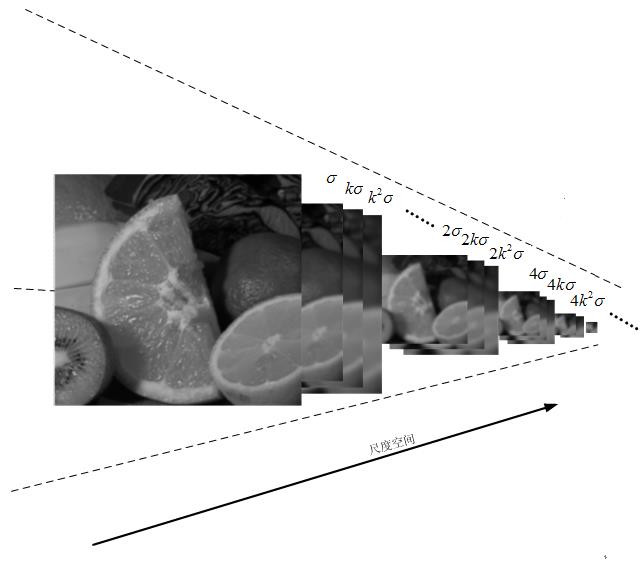
上图中尺度空间中k前的系数n表示的是第一组图像尺寸是当前组图像尺寸的n倍。
上面说这么多,只是得到了一张近似hessian的行列式图,类似SIFT中的DoG图。但是在金字塔图像中分为很多层, 每一层叫做一个octave,每一个octave中又有几张尺度不同的图片。在SIFT算法中,同一个octave层中的图片尺寸(大小)相同,但是尺度不同(模糊程度)不同,而不同的octave层中的图片尺寸也不相同,因为它是由上一层图片将采样得到的。在进行高斯模糊时,SIFT的高斯模板大小是始终不变的,只是在不同的octave之间改变图片的大小。而在SURF中,图片的大小是一直不变的,不同octave层的待检测图片是改变高斯模糊尺寸大小得到的,当然,同一个octave中不同图片用到的高斯模板尺寸也不同。算法允许尺度空间多层图像同时被处理,不需要对图像进行二次抽样,从而提高算法性能。
(2)利用非极大值抑制初步确定特征点
非极大值抑制
非极大值抑制,简称为NMS算法,其思想是搜素局部最大值,抑制极大值。NMS算法在不同应用中的具体实现不太一样,但思想是一样的。非极大值抑制,在计算机视觉任务中得到了广泛的应用,例如边缘检测、人脸检测、目标检测
以目标检测为例:目标检测的过程中在同一目标的位置上会产生大量的候选框,这些候选框相互之间可能会有重叠,此时我们需要利用非极大值抑制找到最佳的目标边界框,消除冗余的边界框。Demo如下图:

左图是人脸检测的候选框结果,每个边界框有一个置信度得分(confidence score),如果不使用非极大值抑制,就会有多个候选框出现。右图是使用非极大值抑制之后的结果,符合我们人脸检测的预期结果。
如何使用非极大值
前提:目标边界框列表及其对应的置信度得分列表,设定阈值,阈值用来删除重叠较大的边界框。
IoU:intersection-over-union,即两个边界框的交集部分除以它们的并集。
非极大值抑制的流程如下:
-
根据置信度得分进行排序
-
选择置信度最高的比边界框添加到最终输出列表中,将其从边界框列表中删除
-
计算所有边界框的面积
-
计算置信度最高的边界框与其它候选框的IoU。
-
删除IoU大于阈值的边界框
-
重复上述过程,直至边界框列表为空。
此步骤和SIFT类似,将经过hessian矩阵处理过的每个像素点与其三维邻域的26个点进行大小比较,如果它是这26个点中的最大值或者最小值,则保留下来,当作初步的特征点。检测过程中使用与该尺度层图像解析度相对应大小的滤波器进行检测。
(3)精确定位极值点
这里也和SIFT算法中类似,采用三维线性插值法得到亚像素级的特征点,同时也去掉那些值小于一定阈值的点,增加极值使检测到的特征点数量减少,最终只有几个特征最强点会被检测出来。
三维线性插值法
內插是数学领域数值分析中的通过已知的离散数据求未知数据的过程或方法。
根据若干离散的数据数据,得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合。这个过程叫做拟合。內插是曲线必须通过已知点的拟合。
1.线性插值
已知坐标 (x0, y0) 与 (x1, y1),要得到 [x0, x1] 区间内某一位置 x 在直线上的值。
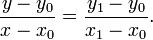
由于 x 值已知,所以可以从公式得到 y 的值
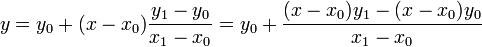
已知 y 求 x 的过程与以上过程相同,只是 x 与 y 要进行交换。
例如,
原来的数值序列:0,10,20,30,40
线性插值一次为:0,5,10,15,20,25,30,35,40
即认为其变化(增减)是线形的,可以在坐标图上画出一条直线 。
线性插值经常用于补充表格中的间隔部分。
两值之间的线性插值基本运算在计算机图形学中的应用非常普遍,以至于在计算机图形学领域的行话中人们将它称为 lerp。所有当今计算机图形处理器的硬件中都集成了线性插值运算,并且经常用来组成更为复杂的运算:例如,可以通过三步线性插值完成一次双线性插值运算。由于这种运算成本较低,所以对于没有足够数量条目的光滑函数来说,它是实现精确快速查找表的一种非常好的方法。
在一些要求较高的场合,线性插值经常无法满足要求。在这种场合,可以使用多项式插值或者样条插值来代替。
线性插值可以扩展到有两个变量的函数的双线性插值。
內插是数学领域数值分析中的通过已知的离散数据求未知数据的过程或方法。
根据若干离散的数据数据,得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合。这个过程叫做拟合。內插是曲线必须通过已知点的拟合。
已知坐标 (x0, y0) 与 (x1, y1),要得到 [x0, x1] 区间内某一位置 x 在直线上的值。
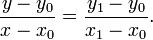
由于 x 值已知,所以可以从公式得到 y 的值
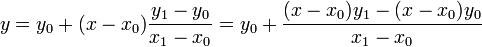
已知 y 求 x 的过程与以上过程相同,只是 x 与 y 要进行交换。
例如,
原来的数值序列:0,10,20,30,40
线性插值一次为:0,5,10,15,20,25,30,35,40
即认为其变化(增减)是线形的,可以在坐标图上画出一条直线 。
线性插值经常用于补充表格中的间隔部分。
两值之间的线性插值基本运算在计算机图形学中的应用非常普遍,以至于在计算机图形学领域的行话中人们将它称为 lerp。所有当今计算机图形处理器的硬件中都集成了线性插值运算,并且经常用来组成更为复杂的运算:例如,可以通过三步线性插值完成一次双线性插值运算。由于这种运算成本较低,所以对于没有足够数量条目的光滑函数来说,它是实现精确快速查找表的一种非常好的方法。
在一些要求较高的场合,线性插值经常无法满足要求。在这种场合,可以使用多项式插值或者样条插值来代替。
线性插值可以扩展到有两个变量的函数的双线性插值。双线性插值经常作为一种粗略的抗混叠滤波器使用,三线性插值用于三个变量的函数的插值。线性插值的其它扩展形势可以用于三角形与四面体等其它类型的网格运算。
2.三线性插值
三线性插值是在三维离散采样数据的张量积网格上进行线性插值的方法。这个张量积网格可能在每一维度上都有任意不重叠的网格点,但并不是三角化的有限元分析网格。这种方法通过网格上数据点在局部的矩形棱柱上线性地近似计算点 (x,y,z) 的值。
- 三线性插值在一次n=1三维D=3(双线性插值的维数:D=2,线性插值:D=1)的参数空间中进行运算,这样需要(1 + n)D = 8个与所需插值点相邻的数据点。
- 三线性插值等同于三维张量的一阶B样条插值。
- 三线性插值运算是三个线性插值运算的张量积。
实例
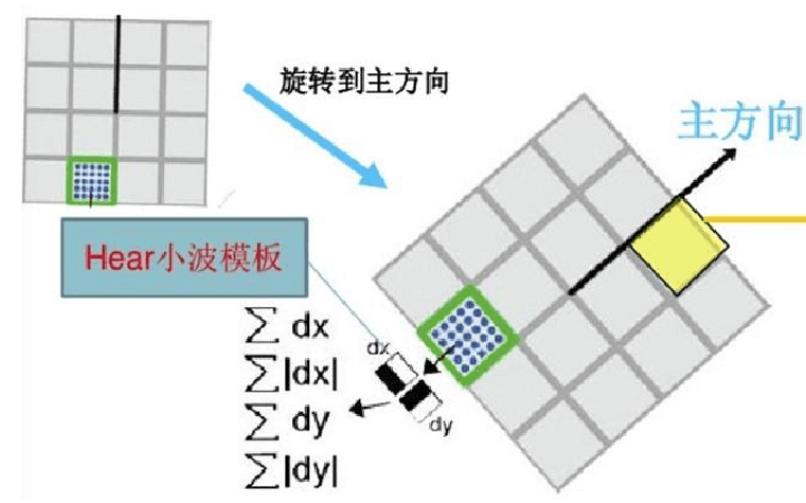
在一个步距为1的周期性立方网格上,取xd,yd,zd 为待计算点,距离小于 x,y,z, 的最大整数的差值,即,
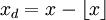
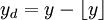
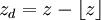
首先沿着z轴插值,得到:
![i_1=v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right],\\times(1-z_d)+v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right]\\times z_d](https://image.cha138.com/20210820/a359b52b6dd64e56857f94c5dd153738.jpg)
![i_2=v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right],\\times(1-z_d)+v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right]\\times z_d](https://image.cha138.com/20210820/2329a6b6beb248a798877e970f5d82f1.jpg)
![j_1=v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right],\\times(1-z_d)+v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right]\\times z_d](https://image.cha138.com/20210820/1087aefc33cf491890fc1fdb0badefaa.jpg)
![j_2=v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right],\\times(1-z_d)+v\\left[\\left\\lfloor x\\right\\rfloor,\\left\\lfloor y\\right\\rfloor\\left\\lfloor z\\right\\rfloor\\right]\\times z_d](https://image.cha138.com/20210820/61d572a9fd48459389075d38c2bf16a0.jpg)
然后,沿着y轴插值,得到:
w1 = i1(1 − yd) + i2yd
w2 = j1(1 − yd) + j2yd
最后,沿着x轴插值,得到:
IV = w1(1 − xd) + w2xd
这样就得到该点的预测值。
三线性插值的结果与插值计算的顺序没有关系,也就是说,按照另外一种维数顺序进行插值,例如沿着 x、 y、z 顺序插值将会得到同样的结果。这也与张量积的交换律完全一致。
(4)选取特征点的主方向
这一步与SIFT也大有不同,SIFT选取特征点主方向是采用在特征点邻域统计其梯度直方图,取直方图bin值最大的以及超过bin值80%的那些方向作为特征点的主方向。
而在SURF中,不统计其梯度直方图,而是统计特征点邻域内的harr小波特征。即在特征点的邻域(比如说,半径为6s的圆内,s为该点所在的尺度)内,统计60度扇形内所有点的水平haar小波特征和垂直haar小波特征总和,haar小波的尺寸变长为4s,这样一个扇形得到了一个值,然后60度扇形以一定间隔进行旋转,最后将最大值那个扇形的方向作为该特征点的主方向。
(5)构造surf特征点描述算子
在SIFT中,是在特征点周围取16x16的邻域,并把该邻域化为4x4个的小区域,每个小区统计8个方向的梯度,最后得到4x4x8=128维的向量,该向量作为该点SIFT描述子。
在SURF中,也是在特征点周围取一个正方形框,框的边长为20s(s是所检测到该特征点所在的尺度)。该框带方向,方向当然就是第(4)步检测出来的主方向了。然后把该框分为16个子区域,每个子区域统计25个像素的水平方向和垂直方向的haar小博特征,这里的水平和垂直方向都是相对主方向而言的。该haar小波特征为水平方向值之和,水平方向绝对值之和,垂直方向之和,垂直方向绝对值之和。这样每个区域就有4个值,所以每个特征点就是16x4=64维向量,相比于SIFT而言,少了一半,这在特征匹配过程中会大大加快匹配速度。
SURF采用Hessian矩阵获取图像局部最值十分稳定,但是在求主方向阶段太过于依赖局部区域像素的梯度方向,有可能使找到的主方向不准确。后面的特征向量提取以及匹配都严重依赖于主方向,即使不大偏差角度也可以造成后面特征匹配的放大误差,从而使匹配不成功。另外图像金字塔的层取得不够紧密也会使得尺度有误差,后面的特征向量提取同样依赖响应的尺度,发明者在这个问题上的折中解决办法是取适量的层然后进行插值。
(6)特征点匹配
Surf通过计算两个特征点间的欧式距离来确定匹配度,欧氏距离越短,代表两个特征点的匹配度越好。Surf还加入了Hesgian矩阵迹的判断,如果两个特征点的矩阵迹正负号相同,代表这两个特征具有相同方向上的对比度变化,如果不同,说明这两个特征点的对比度变化方向是相反的,即使欧氏距离为0,也直接予以排除chong
代码实现:
#include <iostream>
#include <stdio.h>
#include "opencv2/core.hpp"
#include "opencv2/core/utility.hpp"
#include "opencv2/core/ocl.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
#include "opencv2/features2d.hpp"
#include "opencv2/calib3d.hpp"
#include "opencv2/imgproc.hpp"
#include "opencv2/xfeatures2d.hpp"
using namespace cv;
using namespace cv::xfeatures2d;
const int LOOP_NUM = 10;
const int GOOD_PTS_MAX = 50;
const float GOOD_PORTION = 0.15f;
int64 work_begin = 0;
int64 work_end = 0;
static void workBegin()
{
work_begin = getTickCount();
}
static void workEnd()
{
work_end = getTickCount() - work_begin;
}
static double getTime()
{
return work_end /((double)getTickFrequency() )* 1000.;
}
struct SURFDetector
{
Ptr<Feature2D> surf;
SURFDetector(double hessian = 800.0)
{
surf = SURF::create(hessian);
}
template<class T>
void operator()(const T& in, const T& mask, std::vector<cv::KeyPoint>& pts, T& descriptors, bool useProvided = false)
{
surf->detectAndCompute(in, mask, pts, descriptors, useProvided);
}
};
template<class KPMatcher>
struct SURFMatcher
{
KPMatcher matcher;
template<class T>
void match(const T& in1, const T& in2, std::vector<cv::DMatch>& matches)
{
matcher.match(in1, in2, matches);
}
};
static Mat drawGoodMatches(
const Mat& img1,
const Mat& img2,
const std::vector<KeyPoint>& keypoints1,
const std::vector<KeyPoint>& keypoints2,
std::vector<DMatch>& matches,
std::vector<Point2f>& scene_corners_
)
{
//-- Sort matches and preserve top 10% matches
std::sort(matches.begin(), matches.end());
std::vector< DMatch > good_matches;
double minDist = matches.front().distance;
double maxDist = matches.back().distance;
const int ptsPairs = std::min(GOOD_PTS_MAX, (int)(matches.size() * GOOD_PORTION));
for( int i = 0; i < ptsPairs; i++ )
{
good_matches.push_back( matches[i] );
}
std::cout << "\\nMax distance: " << maxDist << std::endl;
std::cout << "Min distance: " << minDist << std::endl;
std::cout << "Calculating homography using " << ptsPairs << " point pairs." << std::endl;
// drawing the results
Mat img_matches;
drawMatches( img1, keypoints1, img2, keypoints2,
good_matches, img_matches, Scalar::all(-1), Scalar::all(-1),
std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS );
//-- Localize the object
std::vector<Point2f> obj;
std::vector<Point2f> scene;
for( size_t i = 0; i < good_matches.size(); i++ )
{
//-- Get the keypoints from the good matches
obj.push_back( keypoints1[ good_matches[i].queryIdx ].pt );
scene.push_back( keypoints2[ good_matches[i].trainIdx ].pt );
}
//-- Get the corners from the image_1 ( the object to be "detected" )
std::vector<Point2f> obj_corners(4);
obj_corners[0] = Point(0,0);
obj_corners[1] = Point( img1.cols, 0 );
obj_corners[2] = Point( img1.cols, img1.rows );
obj_corners[3] = Point( 0, img1.rows );
std::vector<Point2f> scene_corners(4);
Mat H = findHomography( obj, scene, RANSAC );
perspectiveTransform( obj_corners, scene_corners, H);
scene_corners_ = scene_corners;
//-- Draw lines between the corners (the mapped object in the scene - image_2 )
line( img_matches,
scene_corners[0] + Point2f( (float)img1.cols, 0), scene_corners[1] + Point2f( (float)img1.cols, 0),
Scalar( 0, 255, 0), 2, LINE_AA );
line( img_matches,
scene_corners[1] + Point2f( (float)img1.cols, 0), scene_corners[2] + Point2f( (float)img1.cols, 0),
Scalar( 0, 255, 0), 2, LINE_AA );
line( img_matches,
scene_corners[2] + Point2f( (float)img1.cols, 0), scene_corners[3] + Point2f( (float)img1.cols, 0),
Scalar( 0, 255, 0), 2, LINE_AA );
line( img_matches,
scene_corners[3] + Point2f( (float)img1.cols, 0), scene_corners[0] + Point2f( (float)img1.cols, 0),
Scalar( 0, 255, 0), 2, LINE_AA );
return img_matches;
}
// This program demonstrates the usage of SURF_OCL.
// use cpu findHomography interface to calculate the transformation matrix
int main(int argc, char* argv[])
{
const char* keys =
"{ h help | | print help message }"
"{ l left | box.png | specify left image }"
"{ r right | box_in_scene.png | specify right image }"
"{ o output | SURF_output.jpg | specify output save path }"
"{ m cpu_mode | | run without OpenCL }";
CommandLineParser cmd(argc, argv, keys);
if (cmd.has("help"))
{
std::cout << "Usage: surf_matcher [options]" << std::endl;
std::cout << "Available options:" << std::endl;
cmd.printMessage();
return EXIT_SUCCESS;
}
if (cmd.has("cpu_mode"))
{
ocl::setUseOpenCL(false);
std::cout << "OpenCL was disabled" << std::endl;
}
UMat img1, img2;
std::string outpath = cmd.get<std::string>("o");
std::string leftName = cmd.get<std::string>("l");
imread("../1.jpg", IMREAD_GRAYSCALE).copyTo(img1);
if(img1.empty())
{
std::cout << "Couldn't load " << leftName << std::endl;
cmd.printMessage();
return EXIT_FAILURE;
}
std::string rightName = cmd.get<std::string>("r");
imread("../1.jpg", IMREAD_GRAYSCALE).copyTo(img2);
if(img2.empty())
{
std::cout << "Couldn't load " << rightName << std::endl;
cmd.printMessage();
return EXIT_FAILURE;
}
double surf_time = 0.;
//declare input/output
std::vector<KeyPoint> keypoints1, keypoints2;
std::vector<DMatch> matches;
UMat _descriptors1, _descriptors2;
Mat descriptors1 = _descriptors1.getMat(ACCESS_RW),
descriptors2 = _descriptors2.getMat(ACCESS_RW);
//instantiate detectors/matchers
SURFDetector surf;
SURFMatcher<BFMatcher> matcher;
//-- start of timing section
for (int i = 0; i <= LOOP_NUM; i++)
{
if(i == 1) workBegin();
surf(img1.getMat(ACCESS_READ), Mat(), keypoints1, descriptors1);
surf(img2.getMat(ACCESS_READ), Mat(), keypoints2, descriptors2);
matcher.match(descriptors1, descriptors2, matches);
}
workEnd();
std::cout << "FOUND " << keypoints1.size() << " keypoints on first image" << std::endl;
std::cout << "FOUND " << keypoints2.size() << " keypoints on second image" << std::endl;
surf_time = getTime();
std::cout << "SURF run time: " << surf_time / LOOP_NUM << " ms" << std::endl<<"\\n";
std::vector<Point2f> corner;
Mat img_matches = drawGoodMatches(img1.getMat(ACCESS_READ), img2.getMat(ACCESS_READ), keypoints1, keypoints2, matches, corner);
//-- Show detected matches
namedWindow("surf matches", 0);
imshow("surf matches", img_matches);
imwrite(outpath, img_matches);
waitKey(0);
return EXIT_SUCCESS;
}效果图:

补充:
卷积的理解:
用一个例子来说明
如下图所示,输入信号是 f(t) ,是随时间变化的。系统响应函数是 g(t) ,图中的响应函数是随时间指数下降的,它的物理意义是说:如果在 t =0 的时刻有一个输入,那么随着时间的流逝,这个输入将不断衰减。换言之,到了 t =T时刻,原来在 t =0 时刻的输入 f (0)的值将衰减为 f (0) g (T)。
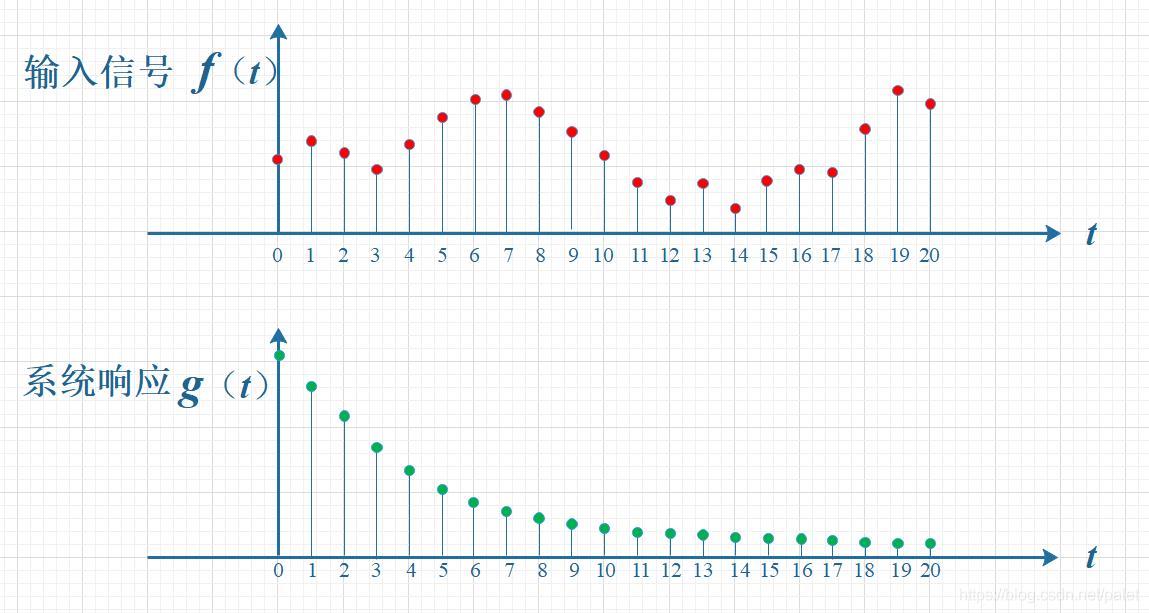
考虑到信号是连续输入的,也就是说,每个时刻都有新的信号进来,所以,最终输出的是所有之前输入信号的累积效果。如下图所示,在T=10时刻,输出结果跟图中带标记的区域整体有关。其中,f(10)因为是刚输入的,所以其输出结果应该是f(10)g(0),而时刻t=9的输入f(9),只经过了1个时间单位的衰减,所以产生的输出应该是 f(9)g(1),如此类推,即图中虚线所描述的关系。这些对应点相乘然后累加,就是T=10时刻的输出信号值,这个结果也是f和g两个函数在T=10时刻的卷积值。
————————————————
原论文的下载链接:
https://download.csdn.net/download/qq_46418503/20432778
部分推导过程:
SURF的特征点检测方法脱胎于 DoH 特征点检测方法, DoH 特征点检测方法计算图像点的Hessian矩阵的行列值来确定该像素点是否为特征点。
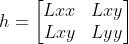
其中,代表高斯正态分布对x的二阶导数与该像素点的卷积值;
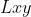 代表高斯正态分布的xy二阶导数与该像素点的卷积值,以此类推
代表高斯正态分布的xy二阶导数与该像素点的卷积值,以此类推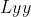 代表高斯正态分布对y的二阶导数与该像素点的卷积值。我们知道Hessian矩阵与多元函数的极值点密切相关。
代表高斯正态分布对y的二阶导数与该像素点的卷积值。我们知道Hessian矩阵与多元函数的极值点密切相关。
1 —如果Hessian矩阵是一个正定矩阵,那么该点是该多元函数的局部极小值点。
2 —如果Hessina矩阵是一个负定矩阵,那么该点是该多元函数的局部极大值点。
3 —如果Hessian矩阵是一个不定矩阵,那么该点不能确定是否为函数的极值点。
当然我们还要清楚一个事实一个函数与高斯正态分布的导数求卷积相当于对该函数直接求导。
所以上述的Hessian矩阵 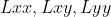 由对应的高斯正态分布的导数与图像的卷积求得与直接对图像点进行求导的意义是一样的,但是SURF方法运用了积分图像与盒子滤波器可以简化运算,盒子滤波器是一种对于高斯正态分布导数的近似。
由对应的高斯正态分布的导数与图像的卷积求得与直接对图像点进行求导的意义是一样的,但是SURF方法运用了积分图像与盒子滤波器可以简化运算,盒子滤波器是一种对于高斯正态分布导数的近似。
对于函数:
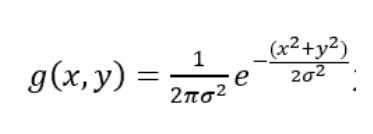
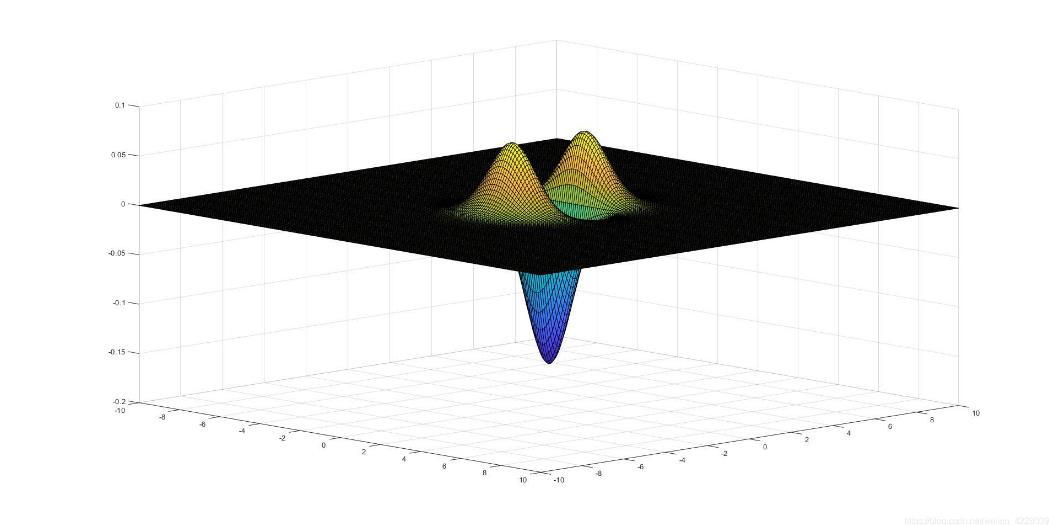
其对x的二阶偏导数:
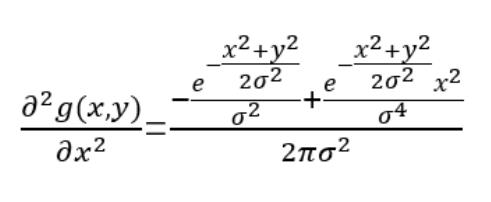
用 matlab 画出二阶偏导数的图像: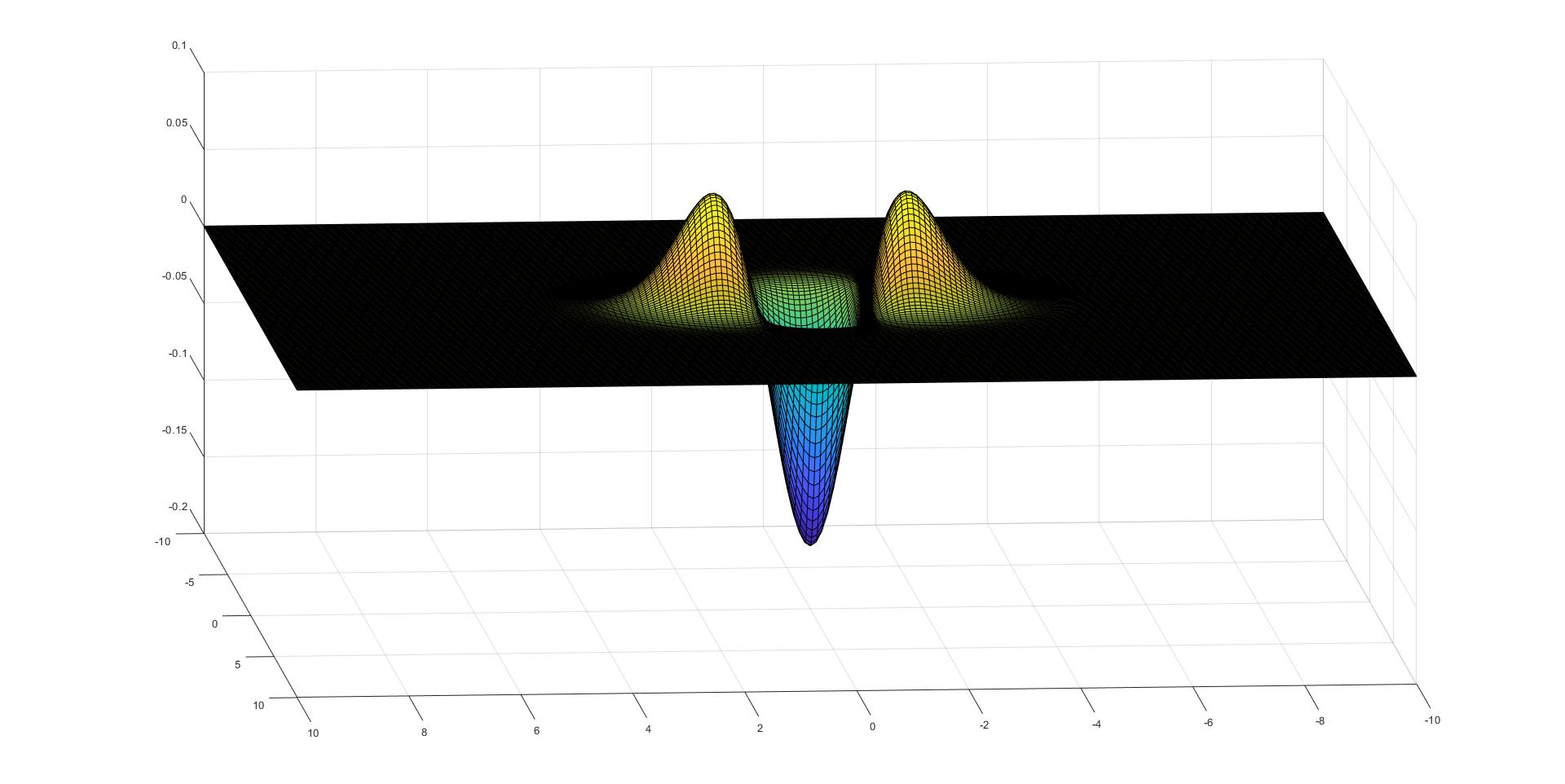
接下来从Z轴方向观察上面的图形: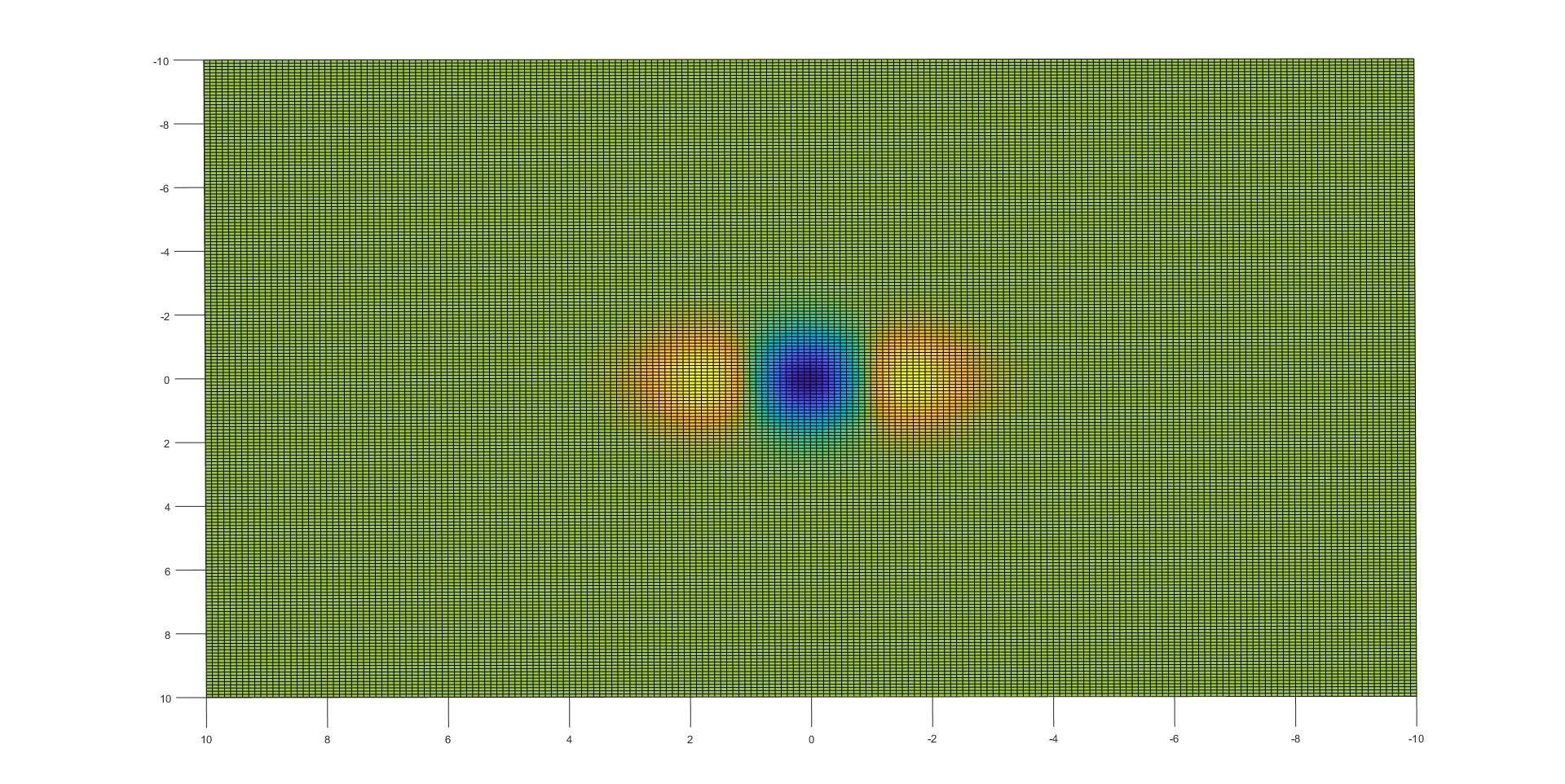
可以发现这就是盒子滤波器的精确版本,但是为了与积分图像结合,论文中对上述图像进行了简化.同样我们可以得  的图像与其盒子滤波器的近似;
的图像与其盒子滤波器的近似;
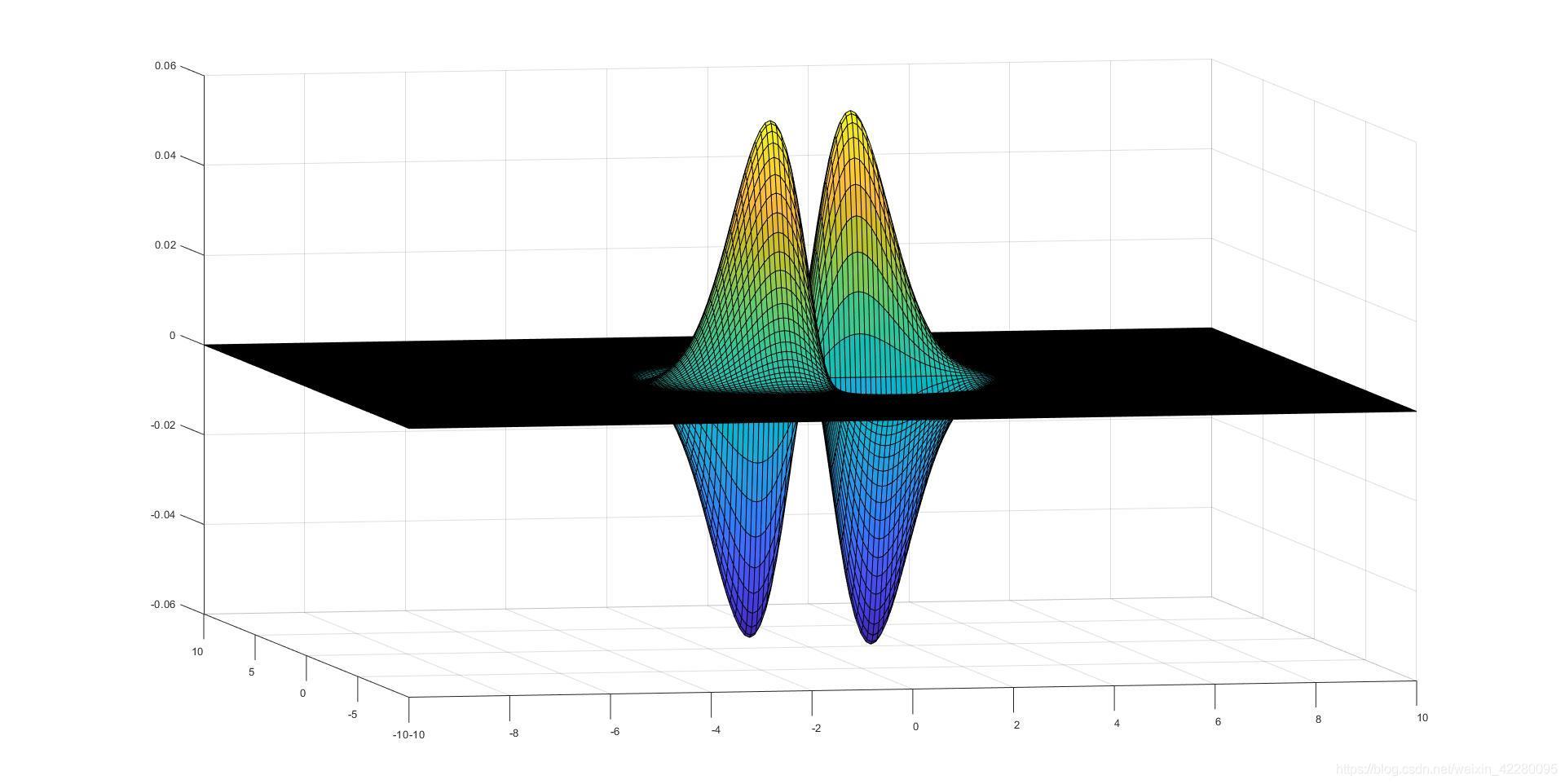
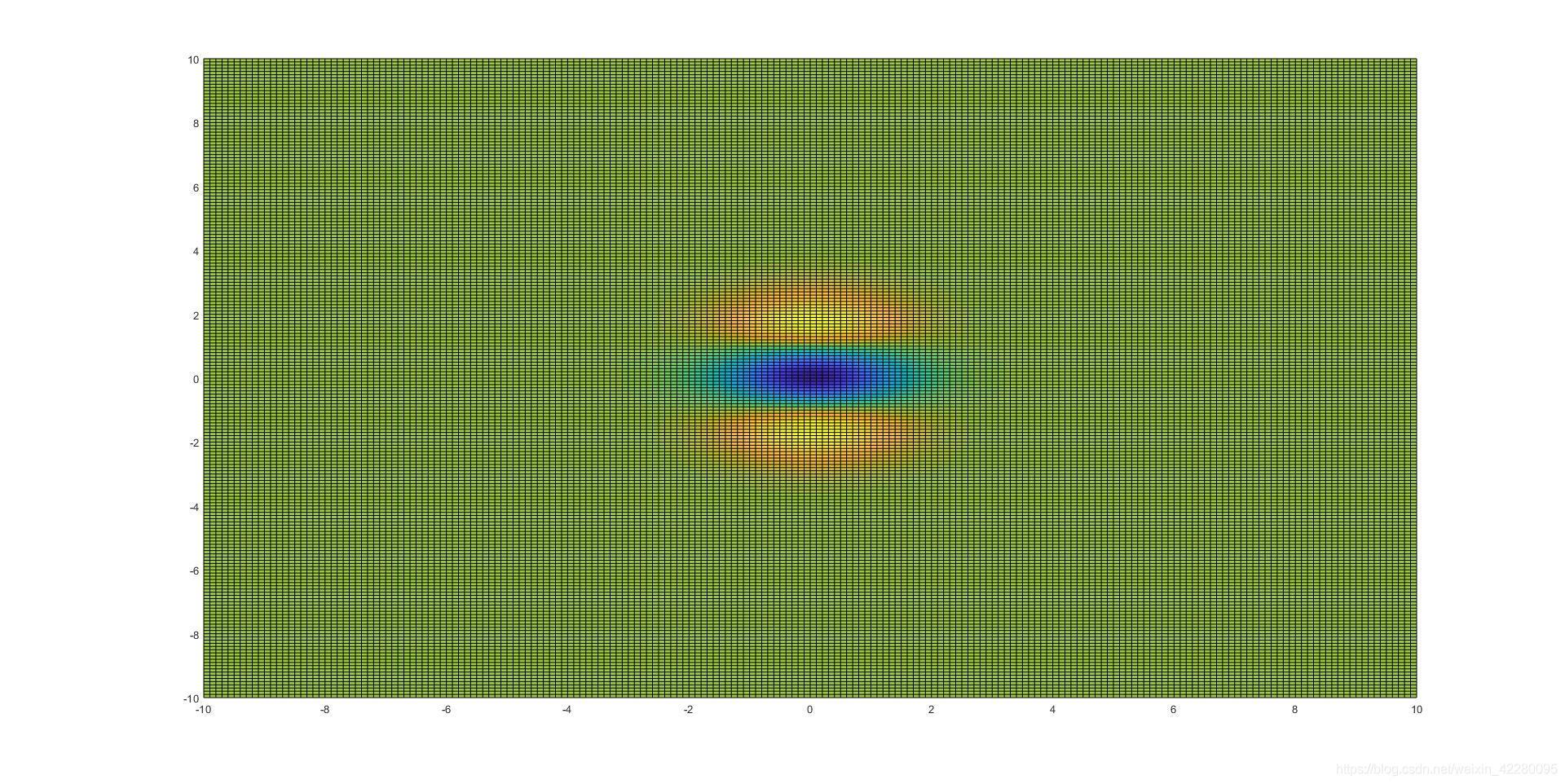
从Z轴观察上述图像分别为:
![]()
![]()
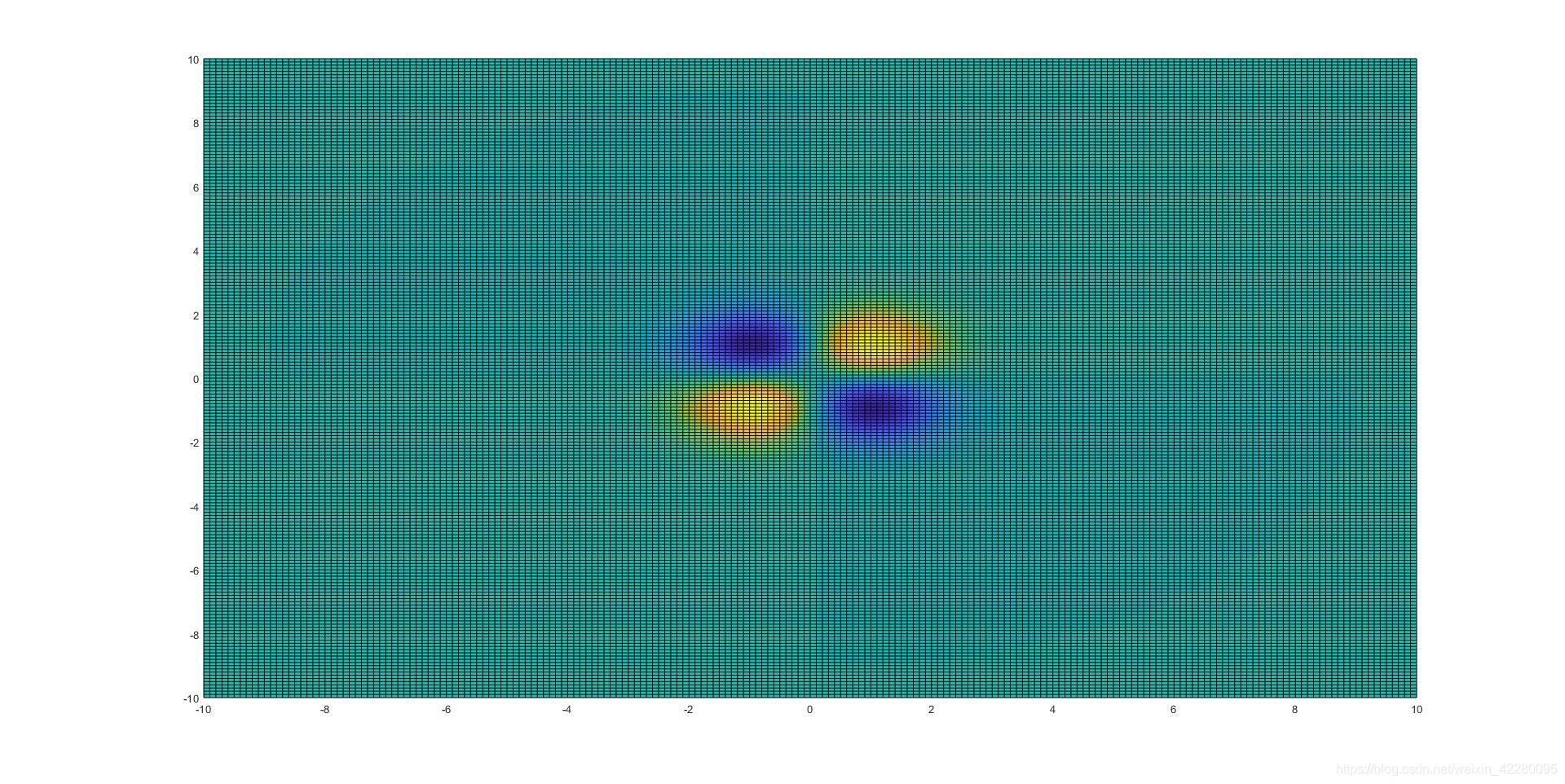
其对应的盒子滤波器的近似图像我们称之为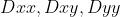
图像如下图所示:
对于公式(1)我们可以得到如下的数学推导:

参考: