C语言数据结构6--队列的实现

Posted 2021-08-19 ZackSock

队列

一、什么是队列

队列同样是一种特殊的线性表，它和栈的阉割方式不一样。它的插入只允许在队尾进行，它的删除只允许在队头进行。因此它有先进先出的特性（FIFO）。

队列和我们日常排队是类似的，相比日常排队，队列是严格禁止插队的。我们可以通过下图来理解队列：

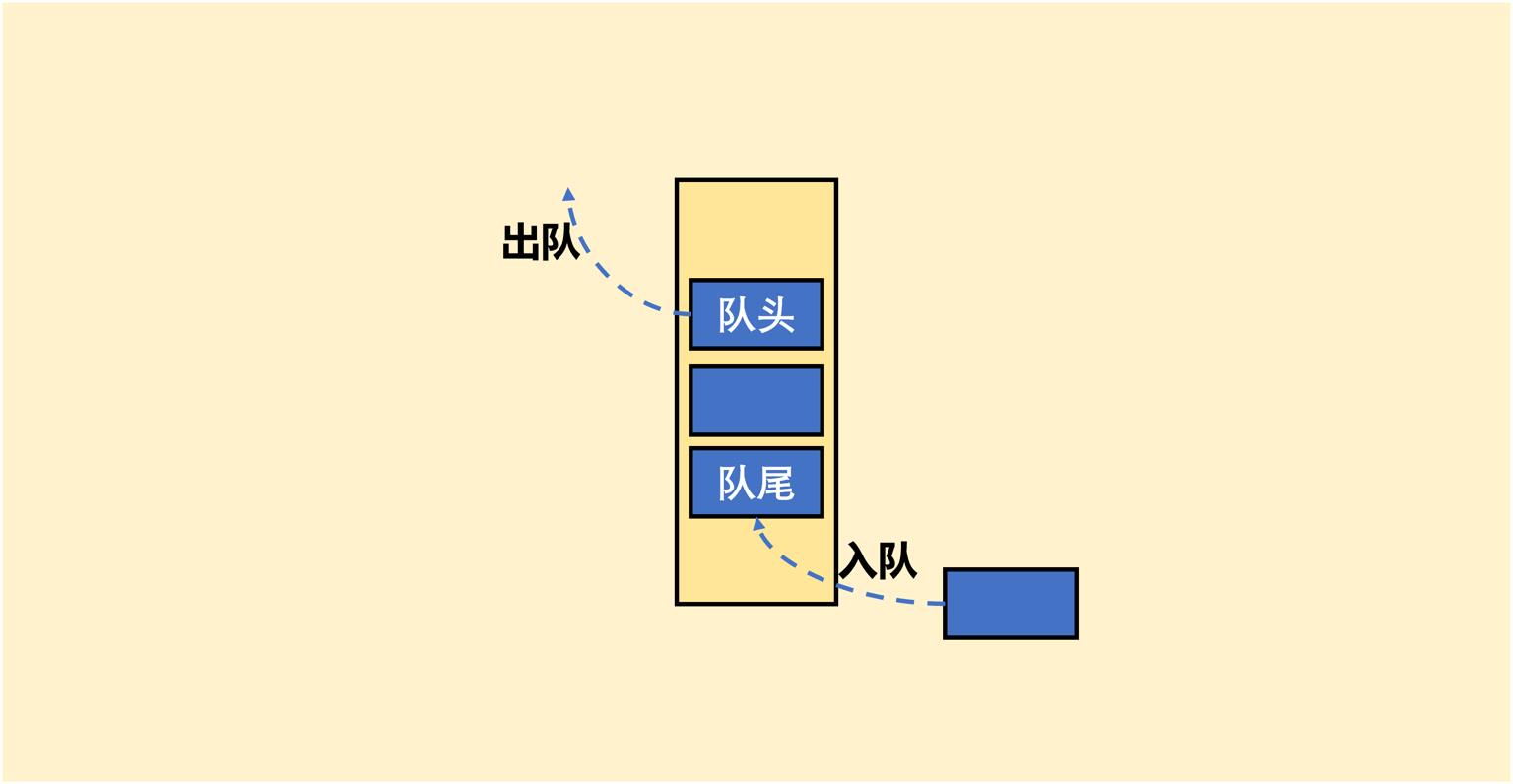
一个队列的第一个元素被称为队头，队列的最后一个元素被称为队尾。队列中最常用的两种操作就是入队和出队，也就是俗称的插入、删除操作。在队列中，只能出队队头元素，入队元素只能在队尾之后。

二、队列的表示

队列同样可以用顺序存储和链式存储两种结构来表示。

（1）顺序存储结构

因为我们要关注队头和队尾的位置，因此我们分别设置对头指针和队尾指针，于是我们结构体的定义如下：

#define MAXSIZE 20
typedef int ElemType;
typedef struct{
    ElemType data[MAXSIZE];		//用静态数组存放队列元素
    int front, rear;		    //队头和队尾指针
}SqQueue;

在使用顺序存储结构实现队列时，我们会构造一个逻辑上循环的队列。后续会有更详细的讲解。

（2）链式存储结构

链式存储结构实现的队列也是一个阉割版的链表，因此它节点的定义和链表是一样的，但是链队列还要额外定义一个队列结构体：

//链队列节点结构体
typedef struct QNode{
    ElemType data;
    struct QNode *next;
}QNode;
//链队列结构体
typedef struct{
    //头尾指针
    QNode *front, *rear;
}LinkedQueue;

链队列的结构体中包含了一个头指针和尾指针。

三、循环队列的实现

（1）循环队列

我们先看看如果没有循环队列的概念，我们应该如何用顺序存储结构实现队列。

在初始状态，我们将队头、队尾指针指向0。在操作队列的过程中，我们保证队头指针指向队头的下标，队尾指针指向队尾的下一个位置。有了这些规则后我们对一个长度为6的队列进行5次入队，5次出队操作，如图示：

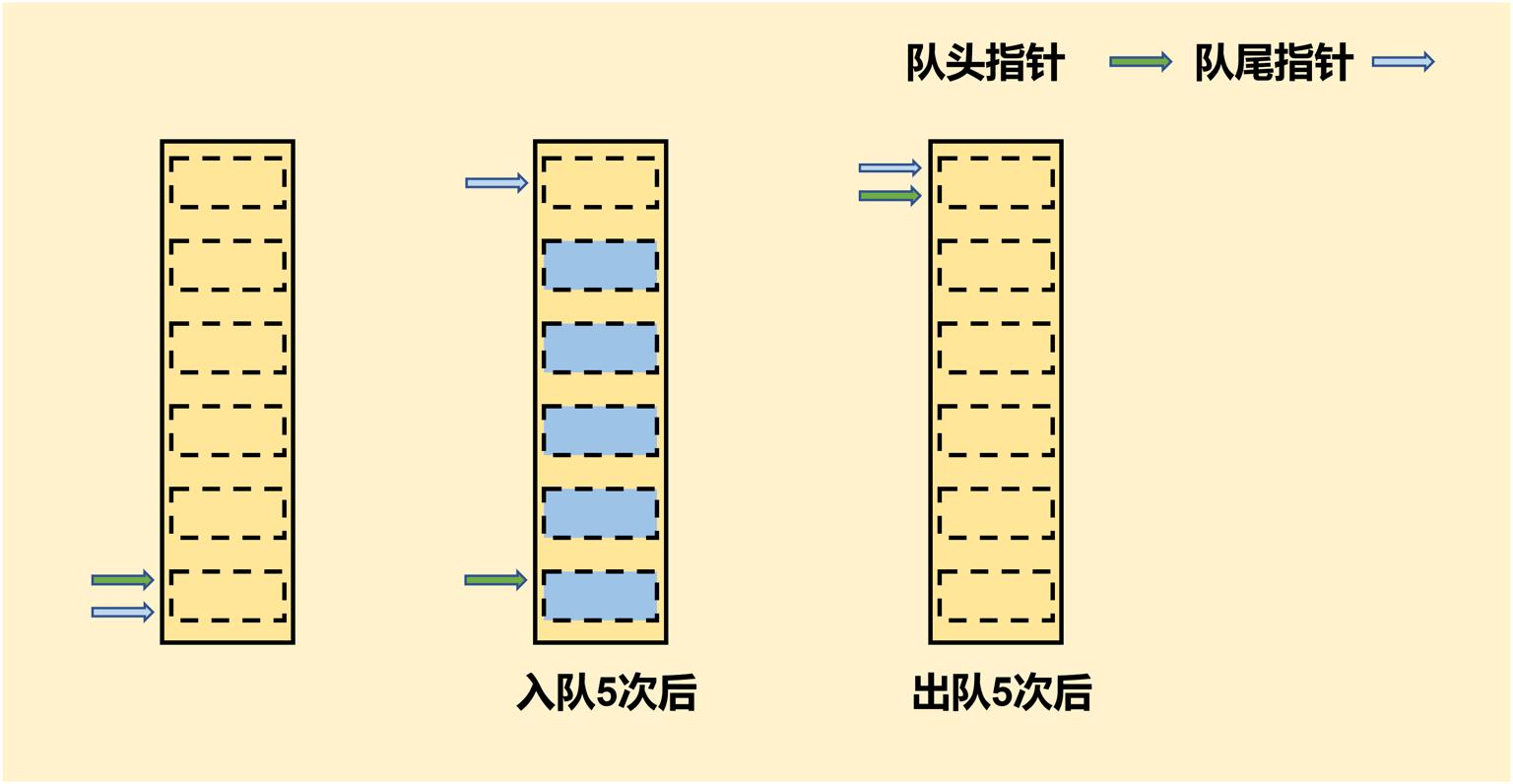
在这个操作过程中，除了队空的情况，队头指针都指向队头元素的位置。而且队空时队头指针等于队尾指针。

我们来关注一下上面的操作我们应该如何判断队满的情况。一种想法是判断尾指针是否等于MAXSIZE-1，但是这样做有个很明显的问题。当我们对一个MAXSIZE=6的队列，入队5次再出队5次后我们的尾指针等于MAXSIZE-1，但是我们队列其实是空的。为了解决这个问题，我们采用循环队列这种逻辑结构。如图示：

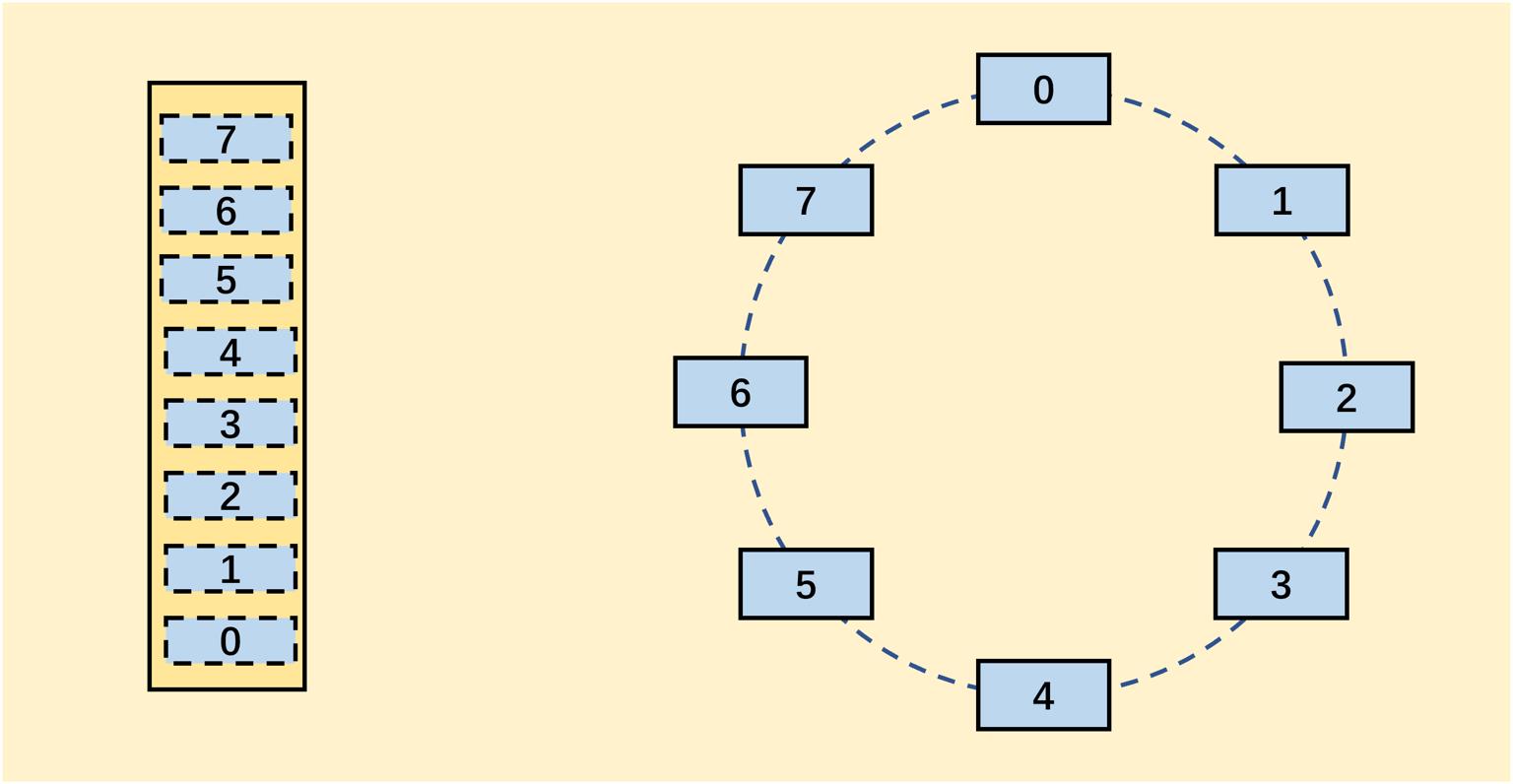
在物理上，我们还是使用一个连续的数组来存储。在逻辑上我们数组的末尾和数组开头是连续的。比如图中末尾下标是7，起始下标为0。因此我们只需要一个可以满足下面要求的公式即可：
$$y=\{\begin{array}{ll}x+1& x<max-1\\ 0& x=max-1\end{array}$$
其中max就表示数组长度。比如最大长度为8，我们的尾指针指向下标7，如果队列还未满，我们入栈则尾指针指向下标0。这很容易让我们想到模运算。因此在我们移动首尾指针时操作应该如下：

Q->rear = (Q->rear + 1) % MAXSIZE;
Q->front = (Q->front + 1) % MAXSIZE;

下面我们就可以着手实现一下循环队列。

（2）队列初始化

队列的初始化我们只需要将首尾指针指向0即可：

int InitSqQueue(SqQueue *Q){
    //首尾指针指向0
    Q->front = Q->rear = 0;
    return 1;
}

因此后续我们判断栈是否为空的依据就是首尾指针是否相等。

（3）判断队列是否为空

当队列为空时，我们返回1，当队列非空时返回0：

int EmptySqQueue(SqQueue Q){
    return Q.rear == Q.front ? 1 : 0;
}

（4）入队操作

入栈操作我们需要先判断队列是否满，如何将输入放入队尾之后：

int EnSqQueue(SqQueue *Q, ElemType elem){
    //如果队列满了，则返回0
    if((Q->rear + 1) % MAXSIZE == Q->front){
        return 0;
    }
    //将元素插入队尾之后
    Q->data[Q->rear] = elem;
    //移动队尾指针
    Q->rear = (Q->rear + 1) % MAXSIZE;
    return 1;
}

（5）出队操作

出队操作和入队相反，我们要判断是否队空，以及操作队头指针：

int DeSqQueue(SqQueue *Q, ElemType *elem){
    //如果队空，则返回0
    if(EmptySqQueue(*Q)){
        return 0;
    }
    //获取队头元素
    *elem = Q->data[Q->front];
    //移动队头元素
    Q->front = (Q->front + 1) % MAXSIZE;
    return 1;
}

其它一些操作这里就不实现了。

四、链队列的实现

链队列和链表十分相似，这里我们简单说一下。

（1）初始化

这里我们选择使用带头节点的链队列：

int InitLinkedQueue(LinkedQueue *Q){
    //创建头节点，让首尾指针指向头节点
    Q->front = Q->rear = (QNode*)malloc(sizeof(QNode));
    //如果内存不足，则返回0
    if(!Q->front){
        return 0;
    }
    //初始化头节点的指针域
    Q->front->next = NULL;
    return 1;
}

（2）判断队空

在初始化时我们把队列首尾指针指向头节点，因此当首尾指针相同时队空：

int EmptyLinkedQueue(LinkedQueue Q){
    return Q.front == Q.rear ? 1 : 0;
}

（3）入队操作

入队操作在队尾进行，因此我们只需要在队尾插入一个元素即可：

int EnLinkedQueue(LinkedQueue *Q, ElemType elem){
    //创建节点
    QNode  *s = (QNode*)malloc(sizeof(QNode));
    //内存不足，则返回0
    if(!s){
        return 0;
    }
    //给节点赋值
    s->data = elem;
    s->next = NULL;
    //在队尾插入节点
    Q->rear->next = s;
    //移动队尾指针
    Q->rear = s;
    return 1;
}

（4）出队操作

出队操作有几个需要注意的点：

1. 队头指针指向的是头节点，因此我们实际要删除的元素是front->next
2. 在队列只剩一个元素时，我们要修改队尾指针

第一点很好理解，我们直接看代码：

int DeLinkedQueue(LinkedQueue *Q, ElemType *elem){
    //如果队空，则返回0
    if(EmptyLinkedQueue(*Q)){
        return 0;
    }
    //定义p指向要删除的元素
    QNode *p = Q->front->next;
    //获取要删除的元素值
    *elem = p->data;
    //移动队头指针
    Q->front->next = p->next;
    //如果删除了最后一个元素，则需要修改队尾指针
    if(Q->rear == p){
        Q->rear == Q->front;
    }
    free(p);
    return 1;
}

我们看下图，此时队列只有一个元素，我们进行出队操作：

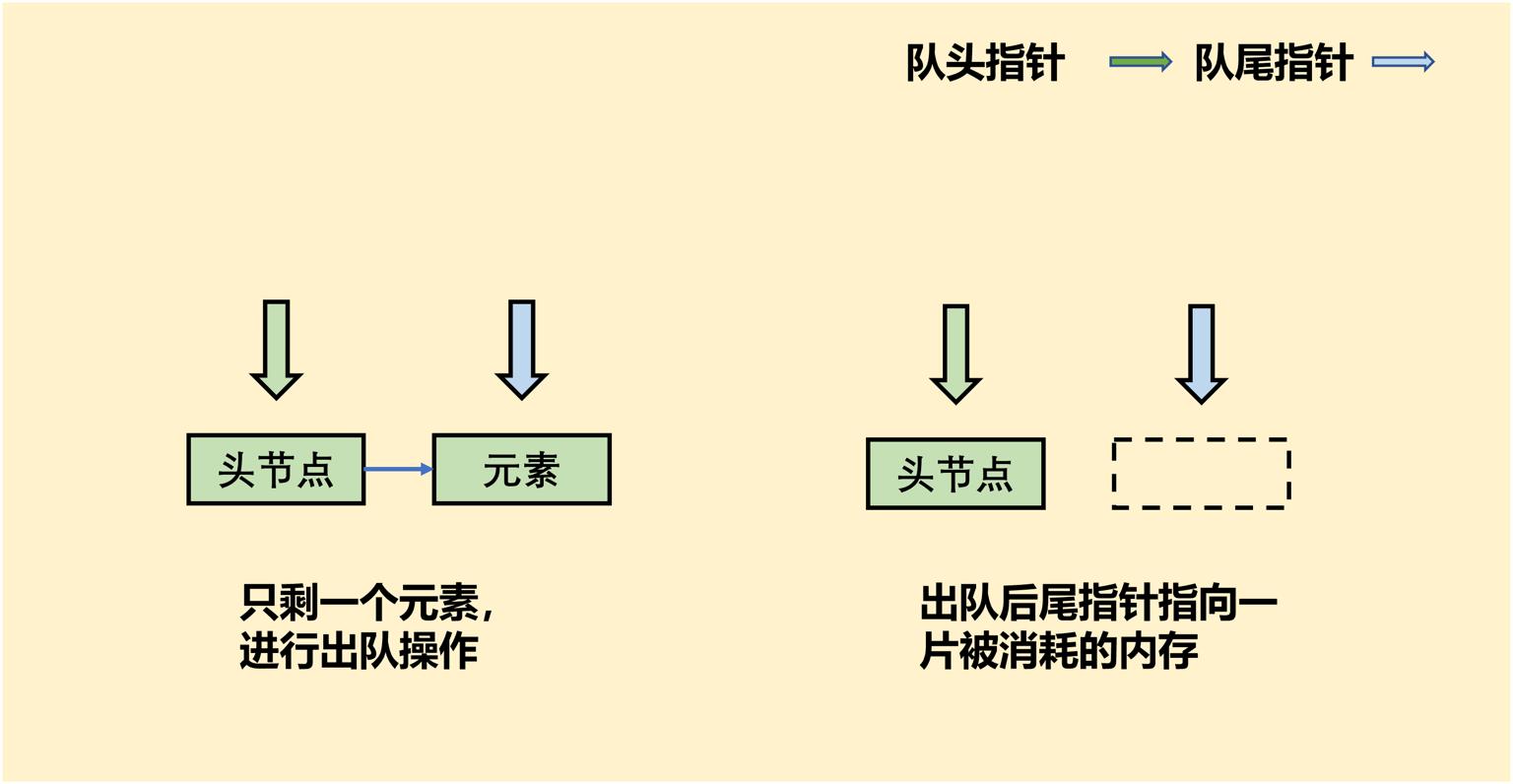
当我们删除最后一个节点后，尾指针指向了一片已经销毁的内存。而且在队列为空的情况，我们的首位指针也不相同。因此我们需要在删除最后一个节点时对队尾指针进行修改。

而判断是否是最后一个节点的条件就是，头节点（Q.front）的next是否是尾节点。

（5）销毁队列

因为我们是使用malloc函数申请的内存，因此我们还需要手动销毁内存：

int DestroyLinkedQueue(LinkedQueue *Q){
    QNode *p = Q->front, *s;
    //判断p是否移动到队尾的next
    while (p){
        //保存当前节点指针
        s = p;
        //p向后移动
        p = p->next;
        //销毁当前节点
        free(s);
    }
    return 1;
}

到此我们就用顺序存储和链式存储两种方式实现了队列。