R假设检验之Bartlett球形检验（Bartlett’s Test of Sphericity）

Posted 2021-08-19 Data+Science+Insight

R假设检验之Bartlett球形检验（Bartlett’s Test of Sphericity）

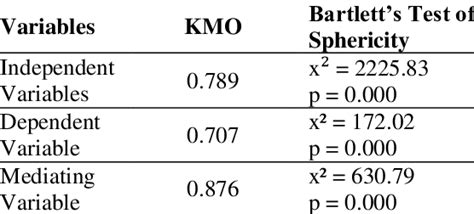
巴特利特球度检验（Bartlett’s Test of Sphericity）将观察到的相关矩阵与单位矩阵进行比较。本质上，它检查变量之间是否存在某种冗余，我们可以用更少的因子来表征这些冗余的信息，说的再直接点就是数据还能继续降维不。

巴特利特球度检验（Bartlett’s Test of Sphericity）的零假设是变量是正交的，即不相关的。另一种假设是，变量不是正交的，即变量这件具有相关性而且相对于单位矩阵具有明显的偏离。

巴特利特球度检验（Bartlett’s Test of Sphericity）通常在我们使用数据降维、压缩（如主成分分析或因子分析）之前进行，以验证数据的压缩或者降维是否具有实际意义。

注：巴特利特的球度检验（Bartlett’s Test of Sphericity）与巴特利特的方差相等检验（Bartlett’s Test for Equality of Variances）不同。这是一个常见的混淆，因为两者有相似的名字。

相关矩阵与单位矩阵

相关矩阵简单地说就是表示变量之间