R假设检验之莫德中位数检验(Mood‘s Median Test)

Posted 2021-08-16 Data+Science+Insight

R假设检验之莫德中位数检验(Mood\'s Median Test)

 

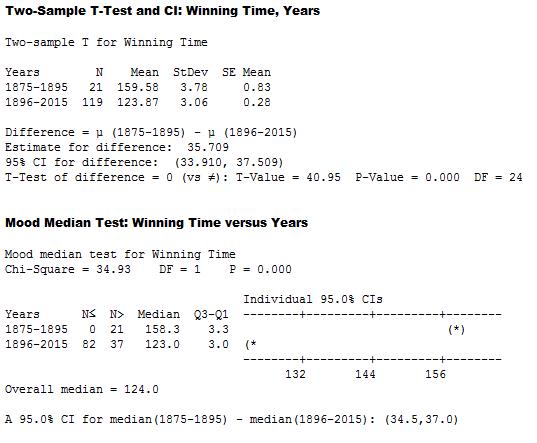
假设检验

假设检验使用统计学中的概念来确定给定假设有效的概率。通过假设检验，我们可以通过分析样本统计量来推断样本对应的总体的参数。

统计假设检验可以分为以下两类：

无效假设（Null Hypothesis）：假设检验是为了检验关于更大人群（总体，population）的主张或假设的有效性而进行的。零假设检验用H0表示。

备则假设（Alternative Hypothesis）：如果无效假设是谬误的，一个备则假设将被认为是有效的。备则假设检验用H1或Ha表示。

让我们以抛硬币为例。我们想断定一枚硬币是不是无偏的。由于零假设是指一个事件的自然状态，因此，根据零假设，如果一枚硬币被抛几次，那么正面和反面出现的次数将是相等的。另一方面，备则假设否定了零假设，指出正面和方面的出现在数量上会有显著的差异。

统计学家使用假设检验来正式检查假设是否被接受或拒绝。假设检验以下列方式进行：陈述假设、制定分析计划、分析样本数据、解释结果&