第七周.01.Tree LSTM带读

Posted 2021-08-18 oldmao_2001

文章目录

• 摘要
• Introduction
• Long Short-Term Memory Networks
• Tree-Structured LSTMs
• • Child-Sum Tree-LSTMs
  • N-ary Tree-LSTMs
• Models

本文内容整理自深度之眼《GNN核心能力培养计划》
公式输入请参考： 在线Latex公式

Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks
这期内容需要有LSTM的基础，没学过LSTM直接看估计又会蒙，所以还是看这里比较容易理解：李宏毅学习笔记13.RNN Part I：
RNN
LSTM
Bi-LSTM
多层LSTM

摘要

从LSTM的特点入手（可以记忆序列的信息），夸夸LSTM的优点（处理序列任务效果好）
Because of their superior ability to preserve sequence information over time, Long Short-Term Memory (LSTM) networks, a type of recurrent neural network with a more complex computational unit, have obtained strong results on a variety of sequence modeling tasks.

再说说LSTM的局限（目前的LSTM主要用在线性的链式结构）
The only underlying LSTM structure that has been explored so far is a linear chain.

转折：自然语言里面存在类似树形的语法属性
However, natural language exhibits syntactic properties that would naturally combine words to phrases.

为了解决这个问题，我们咋做？引入Tree-LSTM
We introduce the Tree-LSTM, a generalization of LSTMs to tree-structured network topologies.

介绍实验结果
Tree-LSTMs outperform all existing systems and strong LSTM baselines on two tasks: predicting the semantic relatedness of two sentences (SemEval 2014, Task 1) and sentiment classification (Stanford Sentiment Treebank).

Introduction

第一段：
先讲词表征的定义：
bag-of-words models
sequence models
tree-structured models
分别讲三种词表征的特点，套路：
In bag-of-words models,。。。。In contrast, 。。。。Lastly,。。。。
第二段：
bag-of-words models属于词序无关的表示方法（Order-insensitive models），缺点是。。。。We therefore turn to后面两种模型。In particular, tree-structured models又比第二种模型好在哪里哪里，最后提出本文的目标，就是要弄出一个Tree LSTM模型来生成tree-structured表征。
第三段：
从模型角度来看，介绍LSTM，及其特点，这段属于过度，因为本文模型是LSTM的扩展。
第四段：
简单介绍本文模型
第五段：
介绍实验

Long Short-Term Memory Networks

原文第二节，这里不展开，相当于Related Work，有两个小节，第一小节介绍LSTM，第二小节介绍LSTM变种：双向LSTM和多层LSTM
关于语法树的例子可以看这里还有这里
StandFord也提供了一些自动生成语法树的工具。
然后在实作的时候，通常要把树转成二叉树，将所有单词都放到叶子节点上。

Tree-Structured LSTMs

先过渡句讲下LSTM有缺点，然后先总后分，总的说明本文模型相对于原始的LSTM有什么改进：

1. the Child-Sum Tree-LSTM
2. the N-ary Tree-LSTM.

然后总体上给出Tree-Structured LSTM的数学表达，比起原始的LSTM，针对树的孩子节点，每个都分配一个遗忘门：
Additionally, instead of a single forget gate, the Tree-LSTM unit contains one forget gate $f_{jk}$ for each child $k$.

这里要说明一下，树和图的关系，学过数据结构的同学应该知道，树其实是图的一种特殊情况，因此将树看做图当然是没有问题的，例如当前节点的邻居当然是他的父节点和子节点，除此之外，还可以加入其他的一些额外的边信息，例如兄弟节点，也可以有二跳邻居：父节点的父节点。

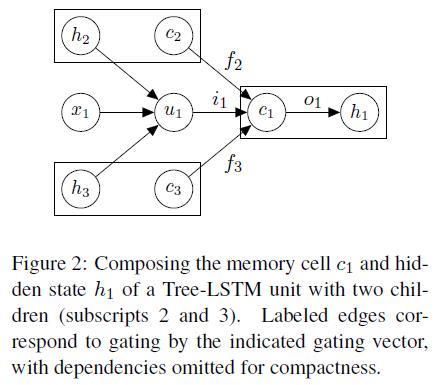
Child-Sum Tree-LSTMs

对于结点$j$而言，$C(j)$表示节点$j$的孩子节点的集合，那么Child-Sum Tree-LSTMs可以表示为：
$${\tilde{h}}_j=\sum _{k\in C(j)}{h}_k$$
就是把所有孩子节点的信息求和（类别GNN的消息汇聚）得到${\tilde{h}}_j$
对于输入门和输出门表达式都直接用孩子节点汇聚的信息进行计算：
$$i_j=\sigma \left(W^{(i)}{x}_j+U^{(i)}{\tilde{h}}_j+b^{(i)}\right)$$
$$o_j=\sigma \left(W^{(o)}{x}_j+U^{(o)}{\tilde{h}}_j+b^{(o)}\right)$$
更新门：
$$u_j=\tanh \left(W^{(u)}{x}_j+U^{(u)}{\tilde{h}}_j+b^{(u)}\right)$$
对于遗忘门，由于每个孩子节点都有，因此每个孩子节点的遗忘门打开程度不一样，这里借鉴了attention机制，如果有孩子节点比较重要，那么忘记少点，反之忘记多点：
$$f_{jk}=\sigma \left(W^{(f)}{x}_j+U^{(f)}{h}_k+b^{(f)}\right)$$
可以看到，由于是针对每一个孩子分别进行计算的，因此用的$h_k$，不是求和结果${\tilde{h}}_j$，这里得到的结果相当于attention里面的权重（遗忘门打开的大小）
然后遗忘门打开的大小计算当前节点$j$的self-state：
$$c_j=i_j\odot u_j+\sum _{k\in C(j)}{f}_{jk}\odot c_k$$
最后算隐藏层状态hidden-state：
$$h_j=o_j\odot \tanh (c_j)$$
最后文章总结了一下3.1，提到这个模型通常用在孩子节点数量较大，且孩子节点无序的情况，这样弄出来的树也叫：dependency tree，整个模型就叫Dependency Tree-LSTM.

N-ary Tree-LSTMs

如果树中节点的子节点数量最大为$N$，那么，且子节点有序，那么可以标识为1到$N$，对于节点$j$可以把他的第$k$个子节点的隐藏状态和当前状态记为$h_{jk}$和$c_{jk}$
对于输入门和输出门表达式都直接用$N$个孩子节点信息进行计算：
$$i_j=\sigma (W^{(i)}{x}_j+\sum _{l=1}^N{U}_l^{(i)}{h}_{jl}+b^{(i)})以上是关于第七周.01.Tree\; LSTM带读的主要内容，如果未能解决你的问题，请参考以下文章$$

第七篇：循环神经网络

lstm维度

lstm和gru哪个好

RNN, LSTM, GRU, SRU, Multi-Dimensional LSTM, Grid LSTM, Graph LSTM系列解读

RNN架构解析LSTM 模型

RNN架构解析LSTM 模型