VRP问题基于人工鱼群求解带时间窗的VRP问题matlab源码
Posted 博主QQ2449341593
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了VRP问题基于人工鱼群求解带时间窗的VRP问题matlab源码相关的知识,希望对你有一定的参考价值。
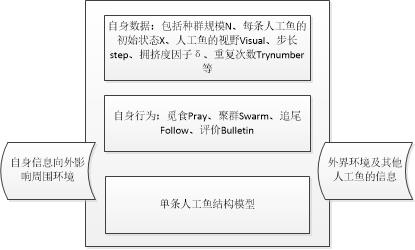
一、 人工鱼的结构模型
人工鱼是真实鱼抽象化、虚拟化的一个实体,其中封装了自身数据和一系列行为,可以接受环境的刺激信息,做出相应的活动。其所在的环境由问题的解空间和其他人工鱼的状态,它在下一时刻的行为取决于自身的状态和环境的状态,并且它还通过自身的活动来影响环境,进而影响其他人工鱼的活动。
二、 人工鱼群算法的寻优原理
人工鱼群算法在寻优的过程中,可能会集结在几个局部最优解的周围,使人工鱼跳出局部最优解,实现全局寻优的因素主要有:
- 觅食行为中重复次数较少时,为人工鱼提供了随机移动的机会,从而可能跳出局部最优解;
- 随机步长使得人工鱼在前往局部最优解的途中,有可能转向全局最优解;
- 拥挤度因子 δδ 限制了聚群的规模,使得人工鱼能够更广泛的寻优;
- 聚群行为能够促使少出陷于局部最优解的人工鱼趋向全局最优解的人工鱼方向聚集,从而逃出局部最优解;
- 追尾行为加快了人工鱼向更优状态游动。
三、 人工鱼群算法实现的步骤
- 初始化设置,包括种群规模N、每条人工鱼的初始位置、人工鱼的视野Visual、步长step、拥挤度因子δ、重复次数Trynumber;
- 计算初始鱼群各个体的适应值,取最优人工鱼状态及其值赋予给公告牌;
- 对每个个体进行评价,对其要执行的行为进行选择,包括觅食Pray、聚群Swarm、追尾Follow和评价行为bulletin;
- 执行人工鱼的行为,更新自己,生成新鱼群;
- 评价所有个体。若某个体优于公告牌,则将公告牌更新为该个体;
- 当公告牌上最优解达到满意误差界内或者达到迭代次数上限时算法结束,否则转步骤3。
四、人工鱼群算法实现流程图

五、 各种参数对收敛性的影响
人工鱼群算法中,觅食行为奠定了算法收敛的基础;聚群行为增强了算法收敛的稳定性;追尾行为增强了算法收敛的快速性和全局性;其评价行为也对算法收敛的速度和稳定性提供了保障。
人工鱼群算法有5个基本参数:群规模N、人工鱼的视野Visual、步长Step、拥挤度因子δ、重复次数Trynumber。
1. 视野Visual:由于视野对算法中个行为都有较大影响,因此,它的变化对收敛性能影响也比较复杂。当视野范围较小时,人工鱼的觅食行为和随机行为比较突出;视野范围较大时,人工鱼的追尾行为和聚群行为将变得比较突出,相应的算法的复杂度也会有所上升。总的来说:视野越大,越容易使人工鱼发现全局最优解并收敛。
2. 步长Step:对于固定步长,随着步长的增加,收敛的速度得到了一定的加速,但在超过一定的范围后,有使得收敛速度减缓,步长过大时会出现震荡现象而大大影响收敛速度。采用随机步长的方式在一定程度上防止了震荡现象的发生,并使得该参数的敏感度大大降低了,但最快的收敛速度还是最优固定步长的收敛速度,所以,对于特定的优化问题,我们可以考虑采用合适的固定步长或者变尺度方法来提高收敛速度。
3. 群规模N:人工鱼的数目越多,跳出局部最优解的能力越强,同时,收敛的速度也越快。当然,付出的代价就是算法每次迭代的计算量也越大,因此,在使用过程中,满足稳定收敛的前提下,应当尽可能的减少个图数目。
4. 尝试次数Trynumber:尝试次数越多,人工鱼的觅食行为能力越强,收敛的效率也越高。在局部极值突出的情况下,应该适当的减少以增加人工鱼随机游动的概率,克服局部最优解。
5. 拥挤度因子δ:在求极大值问题中,δ=1/(αnmax),α∈(0,1]δ=1/(αnmax),α∈(0,1];在求极小值问题中,δ=αnmax,α∈(0,1]δ=αnmax,α∈(0,1]。其中α为极值接近水平, nmax为期望在该邻域内聚集的最大人工鱼数目。拥挤度因子与nf相结合,通过人工鱼是否执行追尾和聚群行为对优化结果产生影响。以极大值为例(极小值的情况正好与极大值相反),δ越大,表明允许的拥挤程度越小,人工鱼摆脱局部最优解的能力越强;但是收敛速度会有所减缓,这主要因为人工鱼在逼近最优解的同时,会因避免过分拥挤而随机走开或者受其他人工鱼的排斥作用,不能精确逼近极值点。可见,虽然δ的引入避免了人工鱼过度拥挤而陷入局部最优解,但是另一方面,该参数会使得位于极值点附件的人工鱼之间存在相互排斥的影响,而难以想极值点精确逼近。所以,对于某些局部极值不是很严重的具体问题,可以忽略拥挤的因素,从而在简化算法的同时也加快算法的收敛速度和提高结果的精确程度。
六、 人工鱼群算法的特点
- 只需比较目标函数值,对目标函数的性质要求不高;
- 对初值的要求不高,随机产生或设置为固定值均可,鲁棒性强;
- 对参数设定的要求不高,容许范围大;
- 收敛速度较慢,但是具备并行处理能力;
- 具备较好的全局寻优能力,能快速跳出局部最优点;
- 对于一些精读要求不高的场合,可以用它快速得到一个可行解;
- 不需要问题的严格机理模型,甚至不需要问题的精确描述,这使得它的应用范围得以延伸。
%
clear
clc
tic %开始计时
c101=importdata('c101.txt'); %用importdata这个函数来读取文件
demand=c101(2:end,4); %需求量
vertexs=c101(:,2:3); %所有点的坐标x和y
customer=vertexs(2:end,:); %顾客坐标
cap=200; %车辆载重量
L=size(customer,1); %顾客数
K=25; %车辆数目
h=pdist(vertexs); %计算顾客之间的距离
D=squareform(h); %计算顾客之间的距离
%% 初始化参数
FishNum=9; %生成10只人工鱼
Max_gen=200; %最多迭代次数
trynumber=500; %最多试探次数
Visual=16; %感知距离
deta=0.8; %拥挤度因子
%% 预处理,确定能使用的车辆最少数目
[minK,chrom_minK,vc_minK,r_minK]=Pre_Deal(L,K,demand,cap);
%% 鱼群初始化,每一行表示一条鱼
initFish=AF_init(FishNum,minK,L);
BestY=zeros(Max_gen,1); %记录每次迭代过程中最优路径的距离
besty=inf; %最优总距离,初始化为无穷大
gen=1;
currX=initFish;
currY=AF_foodconsistence(currX,D,L,minK,demand,cap);
while gen<=Max_gen
for i=1:FishNum
[Xinext,flag]= AF_movestrategy(currX,i,D,Visual,deta,trynumber,L,minK,demand,cap);
currX(i,:)=Xinext;
end
currY=AF_foodconsistence(currX,D,L,minK,demand,cap);
[Ymin,index]=min(currY);
if Ymin<besty
besty=Ymin;
bestx=currX(index,:);
BestY(gen)=besty;
else
BestY(gen)=BestY(gen-1);
end
disp(['第',num2str(gen),'次迭代,得出的最优值:',num2str(BestY(gen))]);
gen=gen+1;
end
figure
plot(1:Max_gen,BestY)
xlabel('迭代次数')
ylabel('优化值')
title('鱼群算法迭代过程')
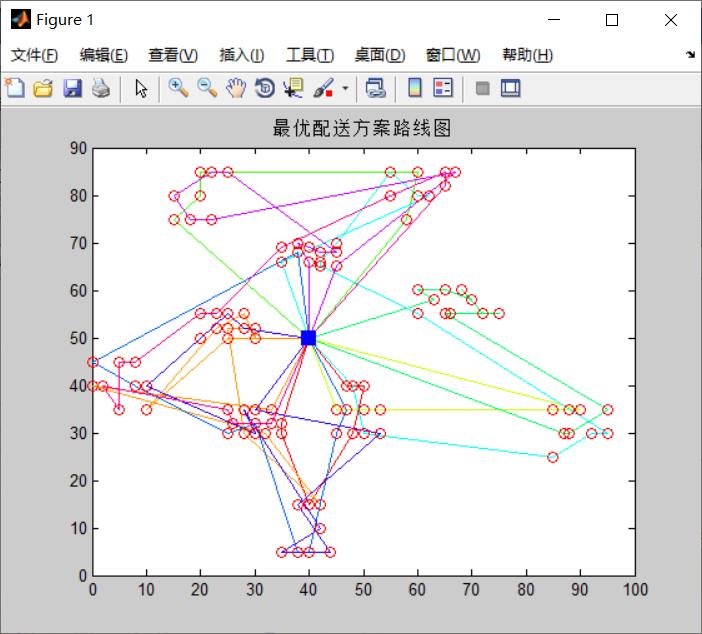
[fvc,reasonable]=Decode(L,minK,bestx,demand,cap);
TD=travel_distance(fvc,D);
toc %结束计时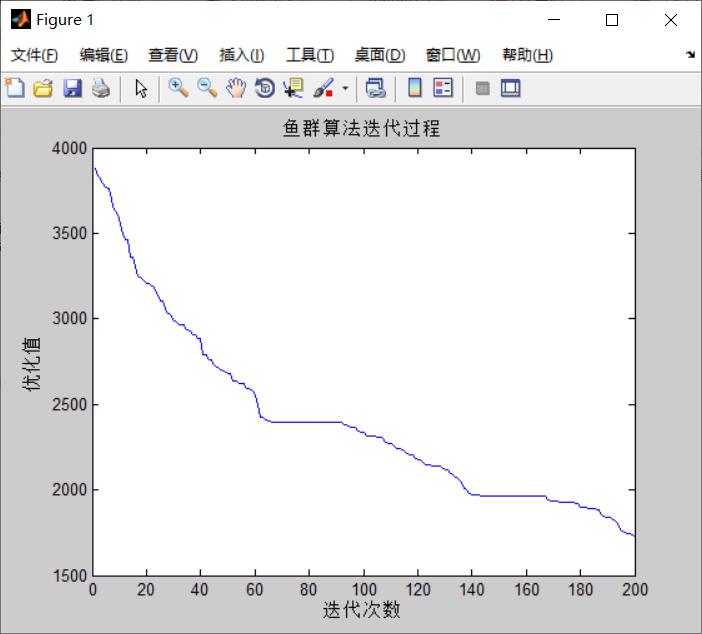
以上是关于VRP问题基于人工鱼群求解带时间窗的VRP问题matlab源码的主要内容,如果未能解决你的问题,请参考以下文章
vrp问题求解基于遗传算法求解带时间窗的车辆路径问题VRPTW
DCTWVRP基于matlab遗传算法求解带容量+距离+时间窗的VRP问题含Matlab源码 1211期