[CF980F]Cactus to Tree
Posted Tan_tan_tann
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[CF980F]Cactus to Tree相关的知识,希望对你有一定的参考价值。
Cactus to Tree
题解
换根dp板子
首先看到这种求出每个节点到叶节点上的最大距离值最小,很容易想到换根。
我们考虑对于一个节点,他什么时候在图上可以使得叶节点与它的距离最小。
很明显对于任意节点,它到其他节点的最短路是不冲突的,我们在这个图上建出它的
b
f
s
bfs
bfs树时一定是最小的,相当于我们要在这个图上再到这个点到其他所有点最短路的最大值。
由于这图保证每个点属于且仅属于一个环,所以它大概是长这样的:
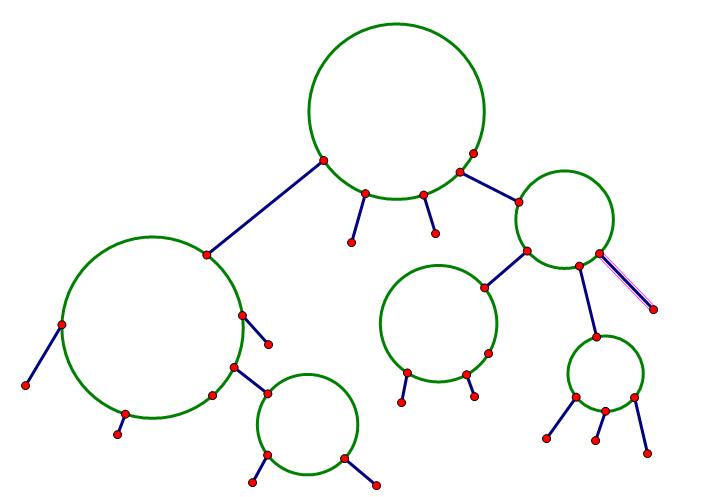
我们可以先以某个点为根,求出每个点到它环外的子树 (其实就是再往下的部分) 上的点的距离最大值。
再对原树进行缩点,将一个环缩成一个点,进行换根。
当换根到某个点时,我们可以将它所属环上的所有点的答案一并求出。
对于这环上的每个点,先暴力枚举其儿子,求出其到它的环外子树中叶节点的距离最大值,再考虑环上点的贡献。
记
g
i
g_{i}
gi表示点
i
i
i的环外子树中叶节点的距离最大值,很明显有,
a
n
s
i
=
max
j
∈
V
(
g
v
+
d
i
s
t
i
,
j
)
ans_{i}=\\max_{j\\in V}\\left(g_{v}+dist_{i,j}\\right)
ansi=j∈Vmax(gv+disti,j)
由于
d
i
s
t
dist
dist在环上分为两段递增,往左往右都是递增,直到环的另一侧与其相对应的点为止。
所以我们可以考虑用单调队列维护环上的点的答案转移。
从一个环换到另一个环时,我们只需要将两环之间桥上在原环上的对应点求出最大值与次大值,看应该去哪一个即可。
注意不能光求子树上的距离,还要注意环上的距离,通过之前求的
a
n
s
ans
ans也就可以得知环上的最大值了。
时间复杂度
O
(
n
+
m
)
O\\left(n+m\\right)
O(n+m)。
不过笔者求环上点时是跟据dfs序排序得到的,所以还要加上一个
l
o
g
log
log。
虽然题目并没有给
m
m
m的范围,但由于一个点只属于一个环可知
m
⩽
3
2
n
m\\leqslant \\frac{3}{2}n
m⩽23n,也就是
n
2
\\frac{n}{2}
2n个二元环构成链是取最大值。
源码
#include<bits/stdc++.h>
using namespace std;
#define MAXN 500005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int inv2=499122177;
const int jzm=2333;
const int orG=3,invG=332748118;
const int lim=300000;
const double Pi=acos(-1.0);
typedef pair<int,int> pii;
const double PI=acos(-1.0);
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y){return x+y<mo?x+y:x+y-mo;}
int qkpow(int a,int s){int t=1;while(s){if(s&1)t=1ll*a*t%mo;a=1ll*a*a%mo;s>>=1;}return t;}
int n,m,head[MAXN],tot,dp[MAXN],g[MAXN],dfn[MAXN],low[MAXN],belong[MAXN];
int sta[MAXN],stak,idx,cnt,q[2][MAXN<<1],Head[2],Tail[2],ans[MAXN];
int dis[MAXN],ord[MAXN],tid,mxd[MAXN];
bool vis[MAXN];
vector<int>cir[MAXN];
queue<int>Q;
struct edge{int to,nxt;}e[MAXN*3];
void addEdge(int u,int v){e[++tot]=(edge){v,head[u]};head[u]=tot;}
void bfs(int s){
while(!Q.empty())Q.pop();Q.push(s);dis[s]=1;vis[s]=1;
while(!Q.empty()){
int t=Q.front();Q.pop();ord[++tid]=t;
for(int i=head[t];i;i=e[i].nxt){
int v=e[i].to;if(vis[v])continue;
Q.push(v);vis[v]=1;dis[v]=dis[t]+1;
}
}
for(int i=tid;i>0;i--){
int u=ord[i];mxd[u]=dis[u];
for(int j=head[u];j;j=e[j].nxt)
mxd[u]=max(mxd[e[j].to],mxd[u]);
dp[u]=mxd[u]-dis[u]+1;
}
}
void tarjan(int u,int fa){
dfn[u]=low[u]=++idx;sta[++stak]=u;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(!dfn[v])tarjan(v,u),low[u]=min(low[u],low[v]);
else if(v!=fa)low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u]){++cnt;int v;do{v=sta[stak--];belong[v]=cnt;}while(v!=u);}
}
void dosaka(int u,int fa){
int id=belong[u],siz=cir[id].size();Head[0]=Tail[0]=Head[1]=Tail[1]=1;
for(int i=0;i<siz;i++){
g[i]=1;
for(int j=head[cir[id][i]];j;j=e[j].nxt)
if(belong[e[j].to]!=id)g[i]=max(dp[e[j].to]+1,g[i]);
}
for(int i=1;i+i<=siz;i++){
while(Head[0]<Tail[0]&&g[i]+i>=g[q[0][Tail[0]-1]]+q[0][Tail[0]-1])Tail[0]--;
q[0][Tail[0]++]=i;
}
for(int i=(siz+1)/2;i<siz;i++){
while(Head[1]<Tail[1]&&g[i]-i>=g[q[1][Tail[1]-1]]-q[1][Tail[1]-1])Tail[1]--;
q[1][Tail[1]++]=i;
}
if(Head[0]<Tail[0])ans[u]=max(ans[u],g[q[0][Head[0]]]+q[0][Head[0]]);
if(Head[1]<Tail[1])ans[u]=max(ans[u],g[q[1][Head[1]]]+siz-q[1][Head[1]]);
for(int i=1;i<siz;i++){
int stp=cir[id][i],las=i-1,lst=(i+(siz+1)/2-1+siz)%siz;
while(Head[1]<Tail[1]&&q[1][Head[1]]==lst)Head[1]++;
while(Head[0]<Tail[0]&&q[0][Head[0]]==i)Head[0]++;
while(Head[1]<Tail[1]&&g[q[1][Tail[1]-1]]+(i+siz-q[1][Tail[1]-1])%siz<=g[las]+(i+siz-las)%siz)Tail[1]--;q[1][Tail[以上是关于[CF980F]Cactus to Tree的主要内容,如果未能解决你的问题,请参考以下文章
构造题 贪心cf1041E. Tree Reconstruction
cf codeforces round#527F. Tree with Maximum Cost树形dp
CF#468 div2 D. Peculiar apple-tree(思维)
CF Round #722 (Div. 2) C. Parsa‘s Humongous Tree(树形dp)