树上骗分: 莫队Ⅲ

Posted 2021-05-19 Wild Donkey

树上莫队 & 括号序

在学习了莫队算法之后, 就得到了一个骗分利器 (虽然经常被强制在线卡掉). 接下来将莫队算法推广到树上, 解决部分树上路径询问问题.

括号序

一棵树用括号来表示, 每个子树被一对括号括起来, 举个例子, 比如这颗树:

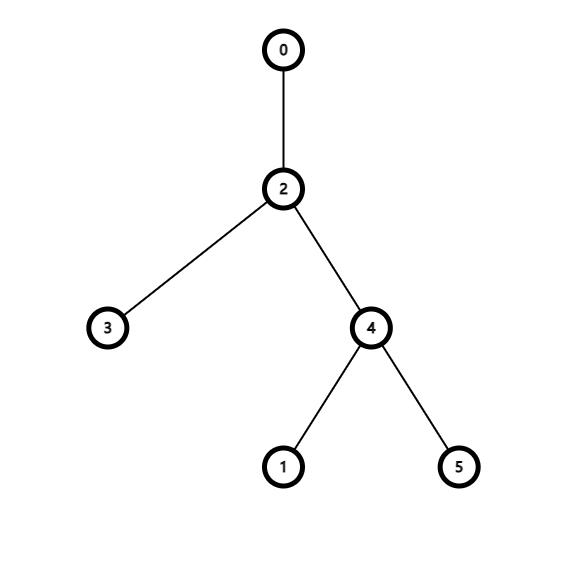
它用括号来表示是这样的:

(( () (() ()) ))

每个节点体现为一对括号, 一个上括号, 一个下括号. 这对括号括起来的括号序列表示的就是这个节点的子树. 在每个上括号后写上它代表的节点, 上面的括号序就变成了这样

(0 (2 (3)(4 (1)(5)) ))

构造括号序很简单, 从根开始对这颗树进行 DFS. 第一次经过时在括号序末尾加一个上括号, 第二次经过是回溯, 这时子树已经遍历, 在序列末尾加上一个下括号.

对于一棵子树对应的括号序, 它们的总和是 \\(0\\). 因为序列中每个上括号和下括号一一对应.

我们将这个得到的括号序列称为欧拉序. 这样就将树的信息转化为了序列的信息, 接下来考虑如何用莫队算法求这个序列的信息.

欧拉序中, 一个点的两个括号出现一个时, 统计它的信息, 出现第二个时消除这个点的信息. 因为这种规则类似于异或, 所以我们可以用一个标记来存储当前区间内, 某个点的括号数量, 每次修改时对 \\(1\\) 异或.

欧拉序有一个性质, 规定一个节点的子树区间是这个点的两个括号之间的闭区间, 则这个区间内 (除端点以外) 的所有括号代表的节点都是这个节点的子节点. 显然, 任意一个点的子树区间的总和都是 \\(0\\), 因为从该节点开始 DFS 到回溯到这个点的过程中, 每个点都被遍历了两次.

由此可以推得两个节点的子树区间不是包含关系就是没有交集. 如果两个节点的括号的相对位置是 A( B( A) B), 则说明两个点存在公共的子节点, 这显然和树的性质相悖.

如果要查询一条路径的信息, 有两种情况, 分类讨论:

• \\(LCA(A, B) = A/B\\)

  不失一般性, 设这个 \\(LCA\\) 就是 \\(A\\). 这时, \\(A\\) 的一对括号将 \\(B\\) 的括号包含了, 所以这时, \\(A\\) 的左括号一定在 \\(B\\) 的左括号前面. 这时我们查询 \\(A\\) 的左括号到 \\(B\\) 的左括号这段闭区间.

  证明这种做法的正确性:

  如果区间中一个点是 \\(A\\) 的儿子, 却不是 \\(B\\) 的祖先, 则这个点的整个子树区间都在选中区间之内, 因为只有遍历完这棵子树, 才能遍历 \\(B\\) 所在的子树, 又因为前面分析了完整的一个子树区间总和为 \\(0\\), 所以这种区间相当于不存在.

  如果区间中一个点是 \\(A\\) 的儿子, 也是 \\(B\\) 的祖先, 这时遍历不完这个点的整个子树就到达了 \\(B\\), 所以这个点只有一个括号在选中区间中. 以此类推, 所有 \\(B\\) 的祖先都会被统计一次, 计入答案, 所以这种统计方式是正确的.

• \\(LCA(A, B) \\neq A/B\\)

  这时, \\(A\\) 和 \\(B\\) 的括号一定互不包含, \\(A\\) 的子树区间和 \\(B\\) 的子树区间无交, 否则就是上面的情况了. 这时不失一般性, 设 \\(A\\) 的子树区间在前. 查询 \\(A\\) 的右括号到 \\(B\\) 的左括号的闭区间, 最后单独计算 LCA 的贡献.

  同样是证明正确性. 对于一个点的多棵子树, 它们的子树区间以任意顺序依次排列在父亲节点的子树区间内. 这时, 选中区间相当于一个跨越了 LCA 的几个儿子的子树区间的一个区间, 其中会包含若干完整的区间, 也会包含 \\(A\\) 所在的 LCA 的某个儿子的子树区间的后缀, 和 \\(B\\) 所在的 LCA 的某个儿子的子树区间的前缀. 在这段区间内, 同样是直系每个点有一个括号被包含, 旁系 (兄弟的子树) 每个点两个括号被包含, 或者不被包含. 所以这段区间查询的是 \\(A\\) 到 \\(B\\) 的路径上除 LCA 之外的点的信息. 最后单独统计 LCA 即可.

模板: SP10707 Count on a tree

给一棵树, 每个节点都有一个颜色, 统计路径上的颜色数量.

离散化颜色, 求树的欧拉序, 在欧拉序上跑莫队, 不要忘了写 LCA, 因为只是求颜色的并, 不是简单相加, 所以查询之后无脑统计 LCA, 不用讨论 LCA 是否被查询到.

这个题贼的很, 虽然口口声声 \\(n \\leq 40000\\), 但是实际上 \\(n\\) 能达到 \\(100000\\), 欧拉序的长度是 \\(2n\\), 最优块长应该是 \\(\\frac {2n}{\\sqrt{m}}\\).

补充一个细节, 太久不写 LCA, 不要忘了在将 \\(x\\), \\(y\\) 跳到同一深度后, 一定要记得特判两点是否重合, 否则会 RE.

最后感谢 SPOJ 的评测姬, 重载运算符的大括号前的 const 没写, 直接给我 CE 了. 这个地方的 const 是玄学, 有时候加了 CE, 有时候不加 CE. (我一开始是加这个 const 的, 结果貌似是被打开 -Wall 的编译器警告了, 所以就不加了, 但是事实证明, 从现在开始我要加这个 const 了).

代码主体:

unsigned a[100005], b[100005], List[100005], m, n, Cnt[100005], CntC(0), CntEu(0), A, B, C, D, t, Ans[100005], Tmp(0), BlockLen;
struct Edge;
struct Node {
  Edge *Fst;
  Node *Fa[18];
  unsigned Val, Dep, Pre, Suf;
  char Have;
}N[100005], *CntN(N), *Ace, *Euler[200005];
struct Edge {
  Node *To;
  Edge *Nxt;
}E[200005], *CntE(E);
struct Qry{
  unsigned Block, L, R, Num;
  inline const char operator<(const Qry &x) const{
    return (this->Block ^ x.Block) ? (this->Block < x.Block) : (this->R < x.R);
  }
}Q[100005];
inline void Link (Node *x, Node *y) {
  (++CntE)->Nxt = x->Fst;
  x->Fst = CntE;
  CntE->To = y;
  return;
}
void DFS (Node *x) {
  Edge *Sid(x->Fst);
  x->Pre = ++CntEu;
  Euler[CntEu] = x;
  while (Sid) {
    if(Sid->To != x->Fa[0]) {
      Sid->To->Fa[0] = x;
      Sid->To->Dep = x->Dep + 1;
      for (register unsigned i(0); Sid->To->Fa[i]; ++i) {
        Sid->To->Fa[i + 1] = Sid->To->Fa[i]->Fa[i];
      }
      DFS(Sid->To);
    }
    Sid = Sid->Nxt;
  }
  x->Suf = ++CntEu;
  Euler[CntEu] = x;
  return;
}
Node *LCA(Node *x, Node *y) {
  if(x->Dep < y->Dep) {
    register Node *Tmp(x);
    x = y, y = Tmp;
  }
  for (register unsigned i(17); x->Dep > y->Dep; --i) {
    if(x->Fa[i]) {
      if(x->Fa[i]->Dep >= y->Dep) {
        x = x->Fa[i];
      }
    }
  }
  if(x == y) {
    return x;
  }
  for (register unsigned i(17); x->Fa[0] != y->Fa[0]; --i) {
    if(x->Fa[i] != y->Fa[i]) {
      x = x->Fa[i];
      y = y->Fa[i];
    }
  }
  return x->Fa[0];
}
int main() {
  n = RD(), m = RD();
  BlockLen = ((n << 1) / (sqrt(m) + 1)) + 1;
  for (register unsigned i(1); i <= n; ++i) {
    a[i] = RD();
  }
  memcpy(b, a, sizeof(a));
  sort(b + 1, b + n + 1);
  for (register unsigned i(1); i <= n; ++i) {
    if(b[i] ^ b[i - 1]) {
      List[++CntC] = b[i];
    }
  }
  for (register unsigned i(1); i <= n; ++i) {
    N[i].Val = lower_bound(List + 1, List + CntC + 1, a[i]) - List;
  }
  for (register unsigned i(1); i < n; ++i) {
    A = RD();
    B = RD();
    Link(A + N, B + N);
    Link(B + N, A + N);
  }
  N[1].Dep = 1;
  N[1].Fa[0] = NULL;
  N[1].Have = 1;
  DFS(N + 1);
  for (register unsigned i(1); i <= m; ++i) {
    A = RD();
    B = RD();
    Q[i].Num = i;
    if((N[A].Pre <= N[B].Pre) && (N[A].Suf >= N[B].Suf)) {//B in A
      Q[i].L = N[A].Pre, Q[i].R = N[B].Pre;
      continue;
    }
    if((N[B].Pre <= N[A].Pre) && (N[B].Suf >= N[A].Suf)) {//A in B
      Q[i].L = N[B].Pre, Q[i].R = N[A].Pre;
      continue;
    }
    Q[i].L = (N[A].Suf < N[B].Suf) ? N[A].Suf : N[B].Suf;
    Q[i].R = (N[A].Pre < N[B].Pre) ? N[B].Pre : N[A].Pre;
  }
  for (register unsigned i(1); i <= m; ++i) {
    Q[i].Block = Q[i].L / BlockLen;
  }
  sort(Q + 1, Q + m + 1);
  Q[0].L = Q[0].R = 1;
  Cnt[Euler[1]->Val] = 1;
  Ans[0] = 1, Euler[1]->Have = 1;
  for (register unsigned i(1); i <= m; ++i) {
    while(Q[0].L > Q[i].L){ // 左端点左移
      if(Euler[--Q[0].L]->Have ^= 1) { // 正标记
        Ans[0] += !(Cnt[Euler[Q[0].L]->Val]++);
      }
      else {                    // 负标记 
        Ans[0] -= !(--Cnt[Euler[Q[0].L]->Val]);
      }
    }
    while(Q[0].R < Q[i].R){ // 右端点右移
      if(Euler[++Q[0].R]->Have ^= 1) { // 正标记
        Ans[0] += !(Cnt[Euler[Q[0].R]->Val]++);
      }
      else {                    // 负标记 
        Ans[0] -= !(--Cnt[Euler[Q[0].R]->Val]);
      }
    }
    while(Q[0].L < Q[i].L){ // 左端点右移
      if(Euler[Q[0].L]->Have ^= 1) { // 正标记
        Ans[0] += !(Cnt[Euler[Q[0].L++]->Val]++);
      }
      else {                  // 负标记 
        Ans[0] -= !(--Cnt[Euler[Q[0].L++]->Val]);
      }
    }
    while(Q[0].R > Q[i].R){ // 右端点左移
      if(Euler[Q[0].R]->Have ^= 1) { // 正标记
        Ans[0] += !(Cnt[Euler[Q[0].R--]->Val]++);
      }
      else {                  // 负标记 
        Ans[0] -= !(--Cnt[Euler[Q[0].R--]->Val]);
      }
    }
    Ans[Q[i].Num] = Ans[0];
    Ans[Q[i].Num] += (!Cnt[LCA(Euler[Q[i].L], Euler[Q[i].R])->Val]);
  }
  for (register unsigned i(1); i <= m; ++i) {
    printf("%u\\n", Ans[i]);
  }
  return Wild_Donkey;
}