22计算机408考研—数据结构—树定义,遍历,Huffman,并查集
Posted 发呆哥o_o ....
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了22计算机408考研—数据结构—树定义,遍历,Huffman,并查集相关的知识,希望对你有一定的参考价值。
手把手教学考研大纲范围内树定义,遍历,Huffman,并查集
22考研大纲数据结构要求的是C/C++,笔者以前使用的都是Java,对于C++还很欠缺,
如有什么建议或者不足欢迎大佬评论区或者私信指出
初心是用最简单的语言描述数据结构
Talk is cheap. Show me the code.
理论到处都有,代码加例题自己练习才能真的学会
树的基本概念
二叉树的基本操作详细解释(非平衡二叉树)
二叉树的 插入 删除(图解+例题)
二叉树的先序,中序,后序遍历(递归)
二叉树的 先 序遍历(图解+例题)
二叉树的 中 序遍历(图解+例题)
二叉树的 后 序遍历(图解+例题)
二叉树的 层 序遍历(图解+例题)
二叉树根据前序遍历,中序遍历构建二叉树,并输出后序遍历
二叉树根据中序遍历,后序遍历构建二叉树,并输出前序遍历
二叉树的例题
Huffman的基本结构和操作
Huffman树的初始化
Huffman编码初始化
并查集
并查集介绍
并查集例题
二叉树顺序存储(完整代码)
二叉树链式存储(完整代码)
Huffman树+编码(完整代码)
树的基本概念
我们还记得线性表是 一个结点连着一个结点
树相对于线性表来说是 一个结点连着多个结点
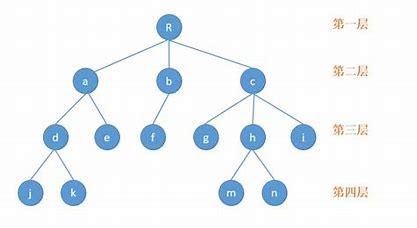
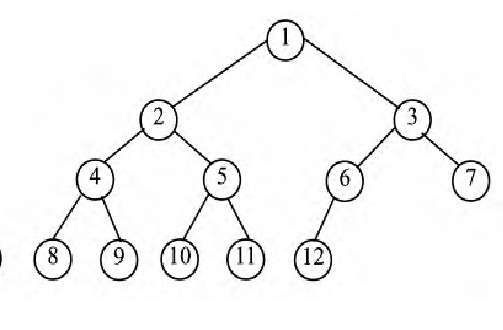
1 结点:树中每一个单元就叫一个结点(例如,R,a,b……)
2 结点的度: 拥有子树的数量,换句话说,一个结点连着几个结点,结点的度就是多少(R连着abc R的度就是3,a连着de a的度就是2)
3 树的度: 树内各个结点的度的最大值(该树的度为3,结点的度最大为3)
4 叶子(终端结点): 度为0的结点称为叶子或者终端结点(叶子为:jkefgmni)
5 非叶子(非终端结点): 度不为0的结点。除根结点外,非终端结点也称为内部结点。
6 双亲和孩子(父结点和子结点): 结点的子树的根称为该结点的孩子,该结点称为孩子的双亲双亲也称为父节点,孩子也称为子结点(abc是R的孩子,R是abc的双亲)
7 兄弟: 同一个双亲(父结点)的孩子之间互称兄弟(ghi互称兄弟)
8 祖先: 从根到该结点所经分支上的所有结点(m的祖先为rch)
9 子孙: 以某结点为根的子树中的任一结点都称为该结点的子孙。(a的子孙为de jk)
10 层次: 根结点为第一层,根结点的孩子为第二层依次向下加……
11 堂兄弟: 双亲在同一层的结点互为堂兄弟。(f的堂兄弟为de ghi)
12 树的深度(高度): 树中结点的最大层次称为树的深度或高度(图示深度为4)
13 有序树和无序树:将数种结点的各子树看成从左到右有次序的(不能互换),则为有序树,否则为无序树 (有序树中最左边的子树的根称为第一个孩子,最右边称为最后一个孩子)
14 森林: m棵互不相交的树的集合,对于每个根结点来说,子树的集合即为森林
15 度,结点,叶子节点的关系:
例题:在一棵度为4的树中,有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,
则树中叶子结点数为?
设n为结点数量,n0为入度为0的结点数量,n1为入度为1的结点数量,……na为入度为a的结点数量
m为总入度数量(总度的数量)
n = n0 + n1…… + na
m = 1 * n1 + 2 * n2 + …… + a * na
n = m + 1
三个关系的解释:
每个结点无非就是: 度为0,度为1,……度为a
把这些结点的数量加起来就是总结点数量
总入度结点为: 各个度×度的数量
例子:度为3的结点代表他有三个子结点,n3代表度为3的结点的数量,3 * n3 代表度为3的结点一共有多少个子孩子
把每个度都按照这种方式加起来,算出来的称作总度
总度,我们算的是子孩子,这里缺少树中的一个根节点(根结点无法通过父结点的度推出),加上根节点即为总结点的数量
例题解析:
n0为度为0的结点,也称作叶子结点
n = n0 + 10 + 1 + 10 + 20
m = 1 * 10 + 2 * 1 + 3 * 10 + 4 * 20
n = m + 1
带入即可得出结果:82
在链式存储中,n个结点的二叉树有n+1个空指针域
(n个结点一共有2n个指针域,除了根结点,这些指针域都包括剩下的结点,也就是说2n个指针域包含 n-1 个结点,剩下的都为空指针域)
16 满二叉树
满二叉树,顾名思义,二叉树已经满了,最后一层是满的,如果在添加只能是在添加一层
满二叉树看起来像是一个三角形
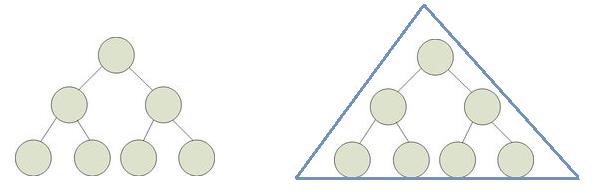
满二叉树的特性:
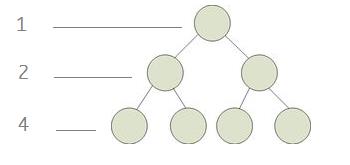
第一层的结点数量为1,
第二层的数量为2
第三层的数量为4
这里可以看作首项为1,公比是2的等比数列
由此可知:
一个层数为K的满二叉树的结点数量:2的K次方 - 1
一个层数为K的满二叉树的叶子结点数量:2的K-1次方
叶结点只能在最后一层
17 完全二叉树
官方解释:
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
换句话说:和满二叉树一样,但是最后一层可能少几个右边的结点,最后一层如果有结点必须靠左
具有n个结点的完全二叉树的深度:[log2k] + 1(注:[ ]表示向下取整)
对一棵完全二叉树有 n 个结点,对任一结点 i(1≤i≤n) 存在:
i=1,则 i 为二叉树的根结点,如果 i>1,则父结点为 i/2
如果 2*i > n ,则 i 结点无左子结点,否则左子结点为 2*i
如果 2*i+1 > n ,则 i 结点无右子结点,否则右子结点为 2*i+1
完全二叉树 的 叶子结点 在 最下层 和 次下层 ,最下层的叶子结点集中在左边,次下层的叶子结点集中在右边
tips: 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
完全二叉树中 叶子结点,非叶子结点,总结点数的关系:
a = 总结点数 / 2 ,b = 总结点数 - a
a 和 b 中大的是叶子结点,小的是非叶子结点
二叉树的基本操作详细解释
每个结点有两个子结点的树
二叉树的插入
以下代码的插入,进入插入方法,从根结点开始,由用户选择左子树和右子树,一直到空结点的位置,根据提示确定插入
插入代码:
//插入结点
bool treeInsert(Tree &tree, int data)
if (tree == NULL) //如果根结点为空,把插入的值插入到根结点
tree = new TreeNode; //添加结点,设置左子结点和右子结点为空
tree->data = data;
tree->leftchild = NULL;
tree->rightchild = NULL;
cout << "根节为点空, 插入成功\\n";
return true;
Tree temp = tree;
while (temp)
cout << "输入 1 选择左子结点,";
cout << "输入 2 选择右子结点,";
cout << "输入 3 返回上一结点,输入 其他 退出插入操作\\n";
int selected;
cin >> selected;
if (selected == 1)
if (temp->leftchild == NULL) //如果左子结点为空,将插入的值放到左子结点
temp->leftchild = new TreeNode;
temp->leftchild->data = data;
temp->leftchild->leftchild = NULL;
temp->leftchild->rightchild = NULL;
cout << "插入成功\\n";
return true;
else //如果左子结点不为空,找到左子结点,继续循环
temp = temp->leftchild;
else if (selected == 2)
if (temp->rightchild == NULL) //右子结点为空,将值插入到右子结点
temp->rightchild = new TreeNode;
temp->rightchild->data = data;
temp->rightchild->leftchild = NULL;
temp->rightchild->rightchild = NULL;
cout << "插入成功\\n";
return true;
else //右子结点不为空,指向右子结点
temp = temp->rightchild;
else //输入其他,自己退出插入操作
return false;
二叉树的删除
和插入差不多的,从根结点开始,用户选择左子树,右子树,或者删除当初结点
删除当前结点,当前结点的子结点会被全部删除
-
顺序存储的是用BFS方法把子树全部删除
链式存储把删除结点的父结点对当前结点的方向的子树附空
删除代码:
//删除子树
bool treeDelete(Tree &tree)
if (tree == NULL) //第一次进来tree为根结点
cout << "根节点为空,无法删除\\n";
return false;
Tree temp = tree;
Tree fathertemp; //记录一下父结点,删除时,把删除结点的父结点的左或者右结点附空
while (true)
if (temp->leftchild != NULL) //删除左子结点或者右子结点的时候判断一下是否为空
cout << "输入 1 选择左子结点,";
if (temp->rightchild != NULL)
cout << "输入 2 选择右子结点,";
cout << "输入 3 删除此结点,输入 其他 退出删除操作\\n";
int selected;
cin >> selected;
if (selected == 1 && temp->leftchild != NULL) //选择左子结点或者右子结点的时候需要判断左子结点或者右子结点是否为空
fathertemp = temp; //转向左子结点或者右子结点的时候,记录一下父结点
temp = temp->leftchild;
else if (selected == 2 && temp->leftchild != NULL)
fathertemp = temp;
temp = temp->rightchild;
else if (selected == 3)
if (fathertemp->leftchild == temp) //删除结点如果是父结点的左结点,就把父结点的左结点附空
fathertemp->leftchild = NULL;
if (fathertemp->rightchild == temp) //右结点同理
fathertemp->rightchild = NULL;
Tree t = temp; //保存一下待删除结点,把待删除结点delete,释放空间
temp = NULL;//直接指向NULL为什么不能删除????????????
delete t;
return true;
else
return false; //输入其他,退出删除操作
二叉树的先序,中序,后序遍历(递归)
递归就是不断的循环调用自己,换一个参数调用自己
对于这三种遍历,不过是左结点,右结点,根结点的访问顺序不一样,其他的都是一样的
当结点为空时,返回结点,当结点不为空,就找左子树右子树,
先序遍历
//前序遍历(递归)
void treePreRecursionPrint(Tree tree) //先输出根结点,在找左结点,在找右结点
if (tree != NULL)
cout << tree->data << " ";
treePreRecursionPrint(tree->leftchild);
treePreRecursionPrint(tree->rightchild);
中序遍历
//中序遍历(递归)
void treeMidRecursionPrint(Tree tree) //先输出左结点,在输出根结点,输出右结点
if (tree != NULL)
treeMidRecursionPrint(tree->leftchild);
cout << tree->data << " ";
treeMidRecursionPrint(tree->rightchild);
后序遍历
//后序遍历(递归)
void treePostRecursionPrint(Tree tree) //先输出左子结点,在输出右子结点,输出根结点
if (tree != NULL)
treePostRecursionPrint(tree->leftchild);
treePostRecursionPrint(tree->rightchild);
cout << tree->data << " ";
二叉树的前(先)序遍历(非递归)
递归方法代码里面有注释
前序遍历:先输出根结点,在输出左结点,在输出右结点
使用栈,栈后进先出,从根结点向下添加,先把下面的输出,然后在一步一步向上走
先把根结点添加,
然后输出结点的值,结点压栈,找此结点的左子树,重复这个操作一直找到左子树为空的时候
然后从栈里弹出结点,此时弹出的结点为上面最后一个左子树为空的结点(栈后进先 出)
使用弹出结点的右结点循环上面的操作,
LeetCode二叉树前(先)序遍历图解:
1 初始状态
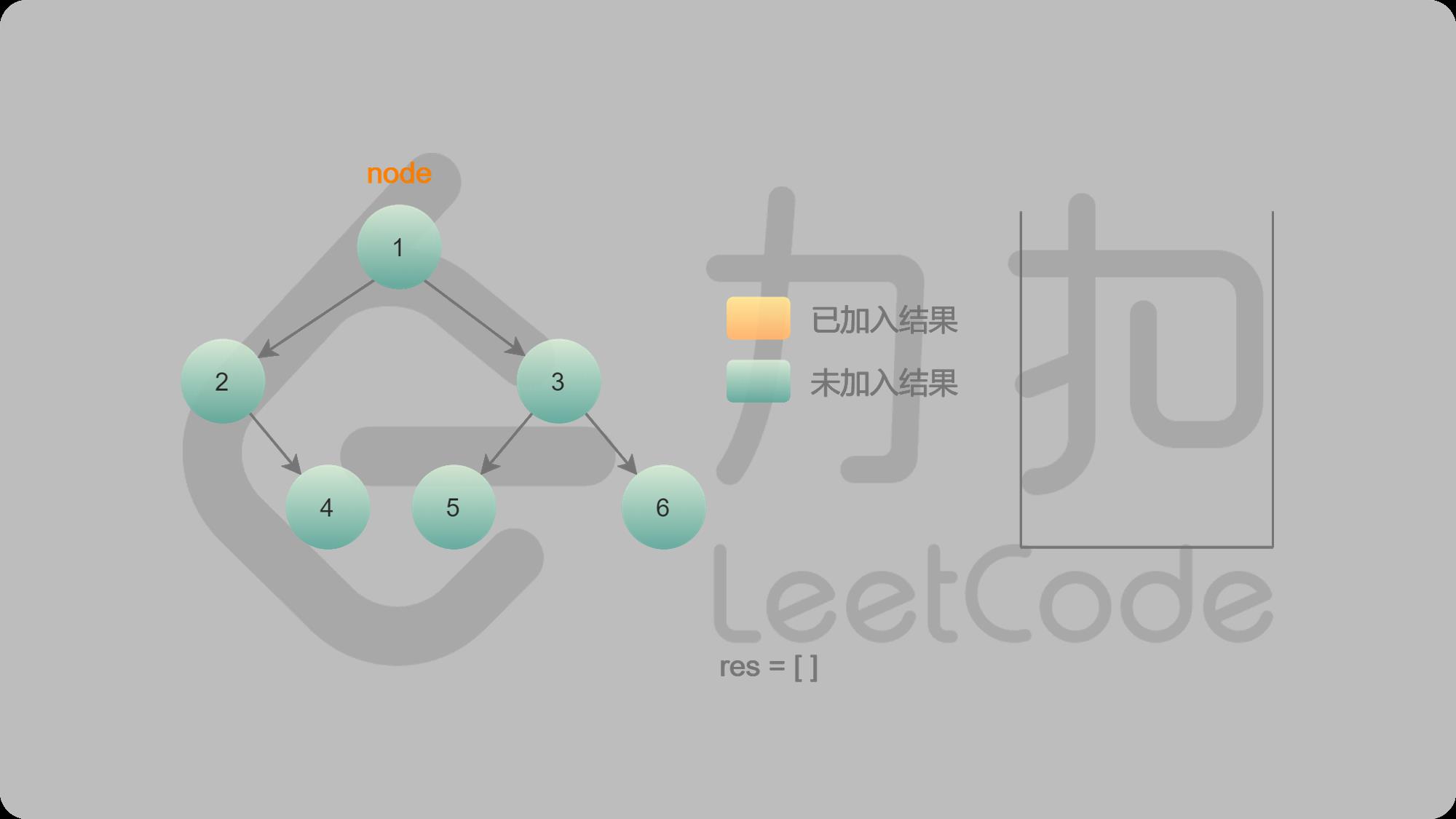
2 1入栈并输出,然后找左子结点
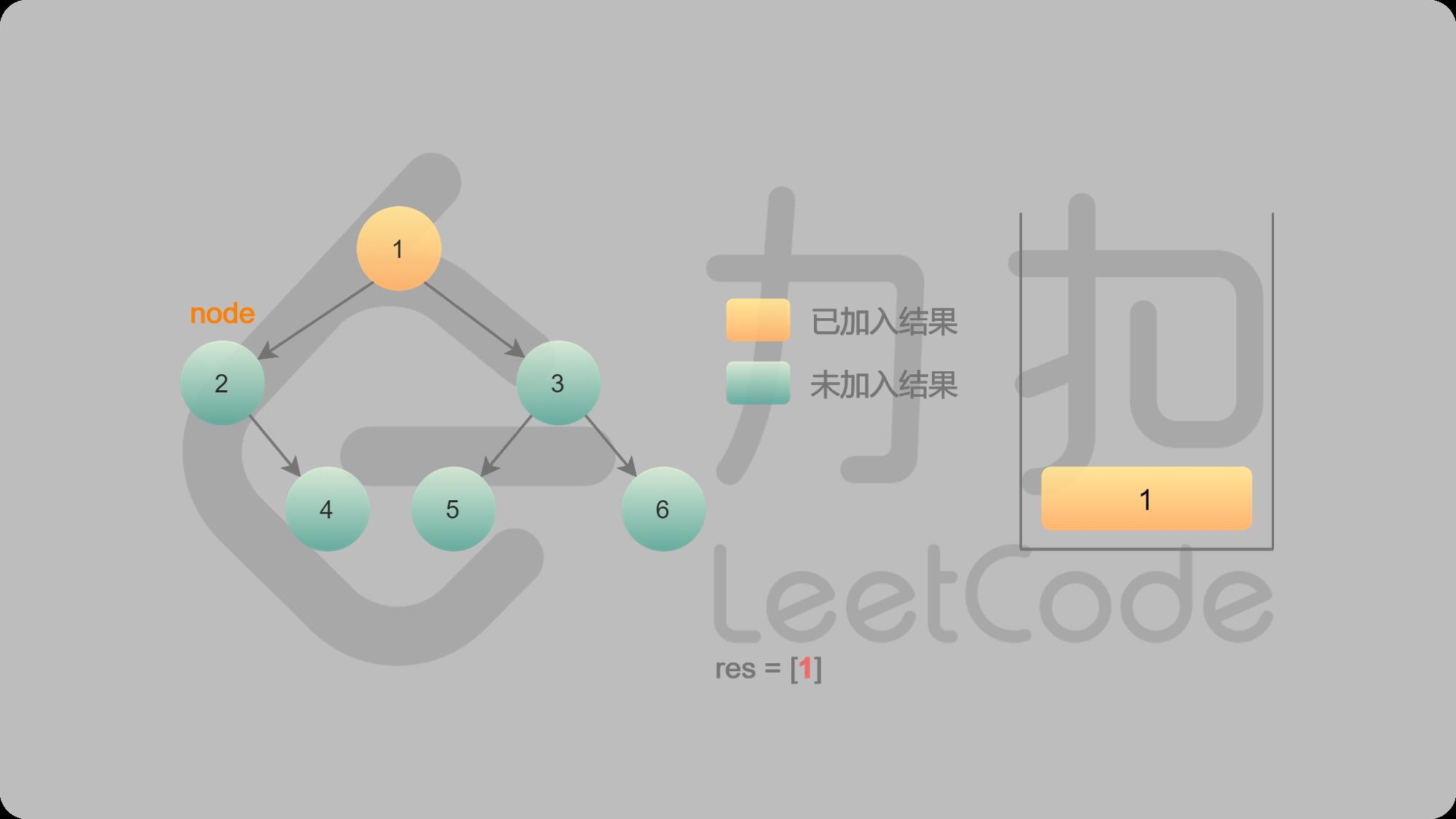
3 2入栈并输出,接着找2的左子结点,但是2没有左子结点
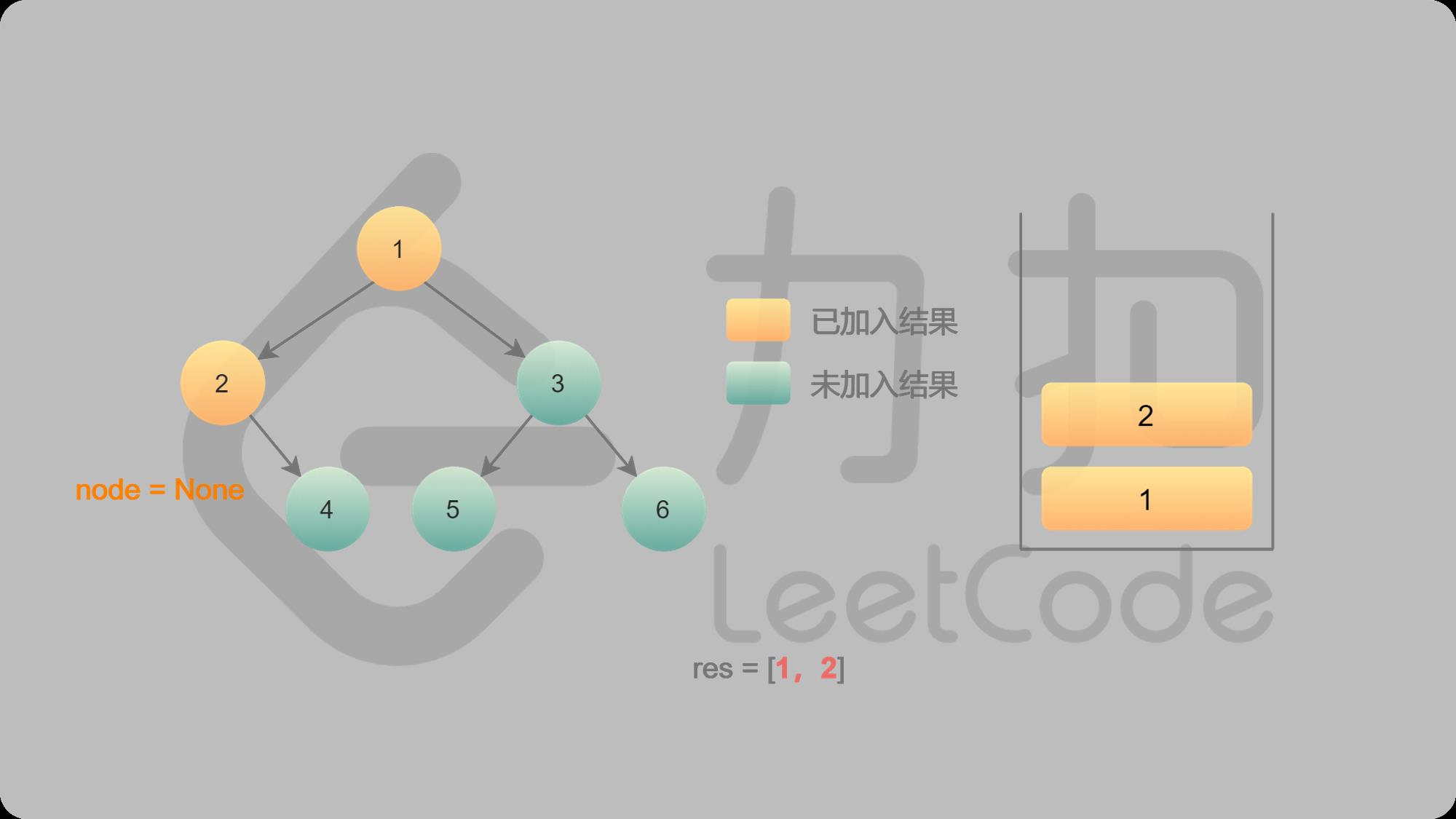
4 2没有左子结点,2出栈,找2的右子结点4
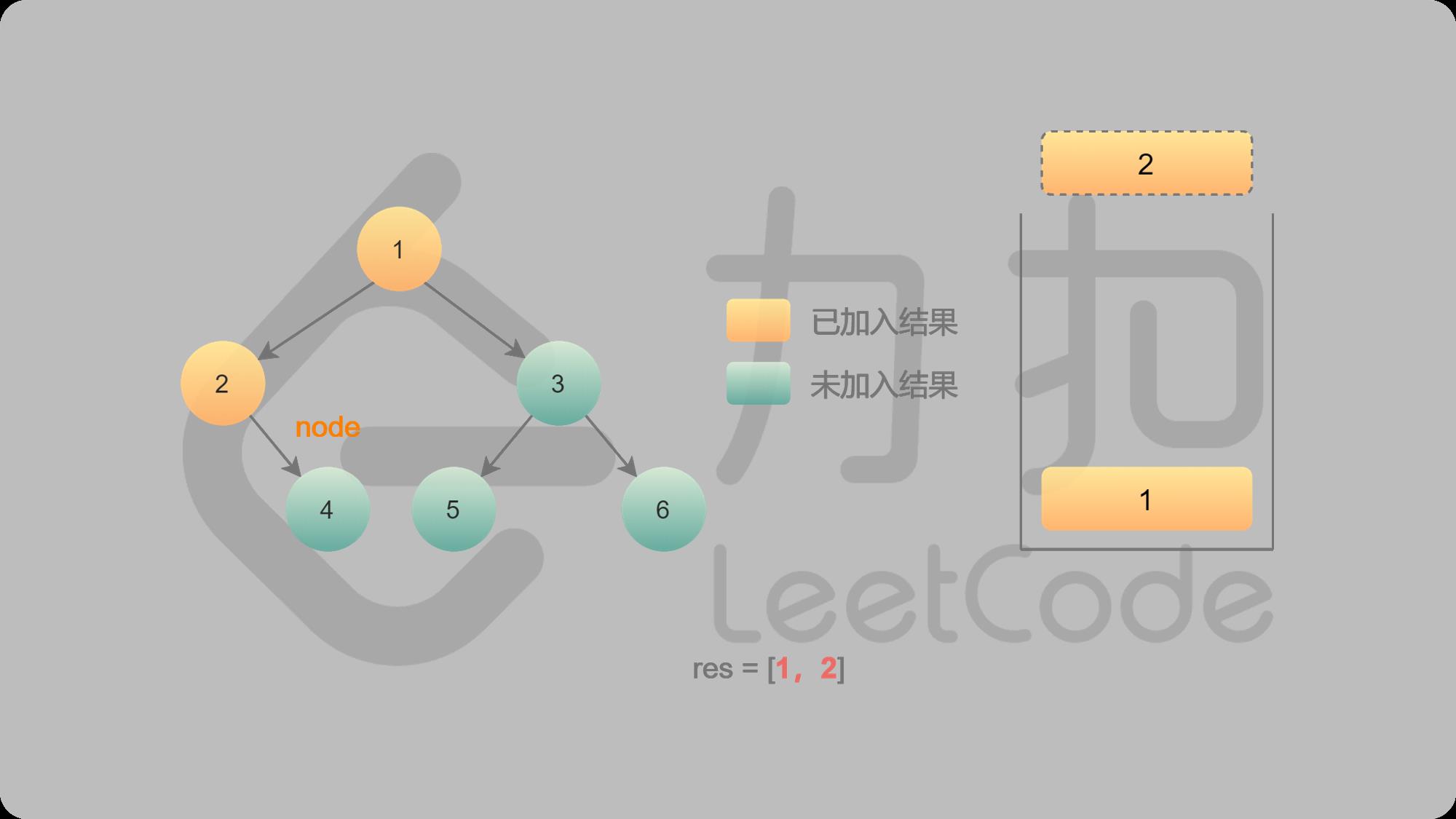
5 4入栈并输出,找4的左子结点,左结点不存在
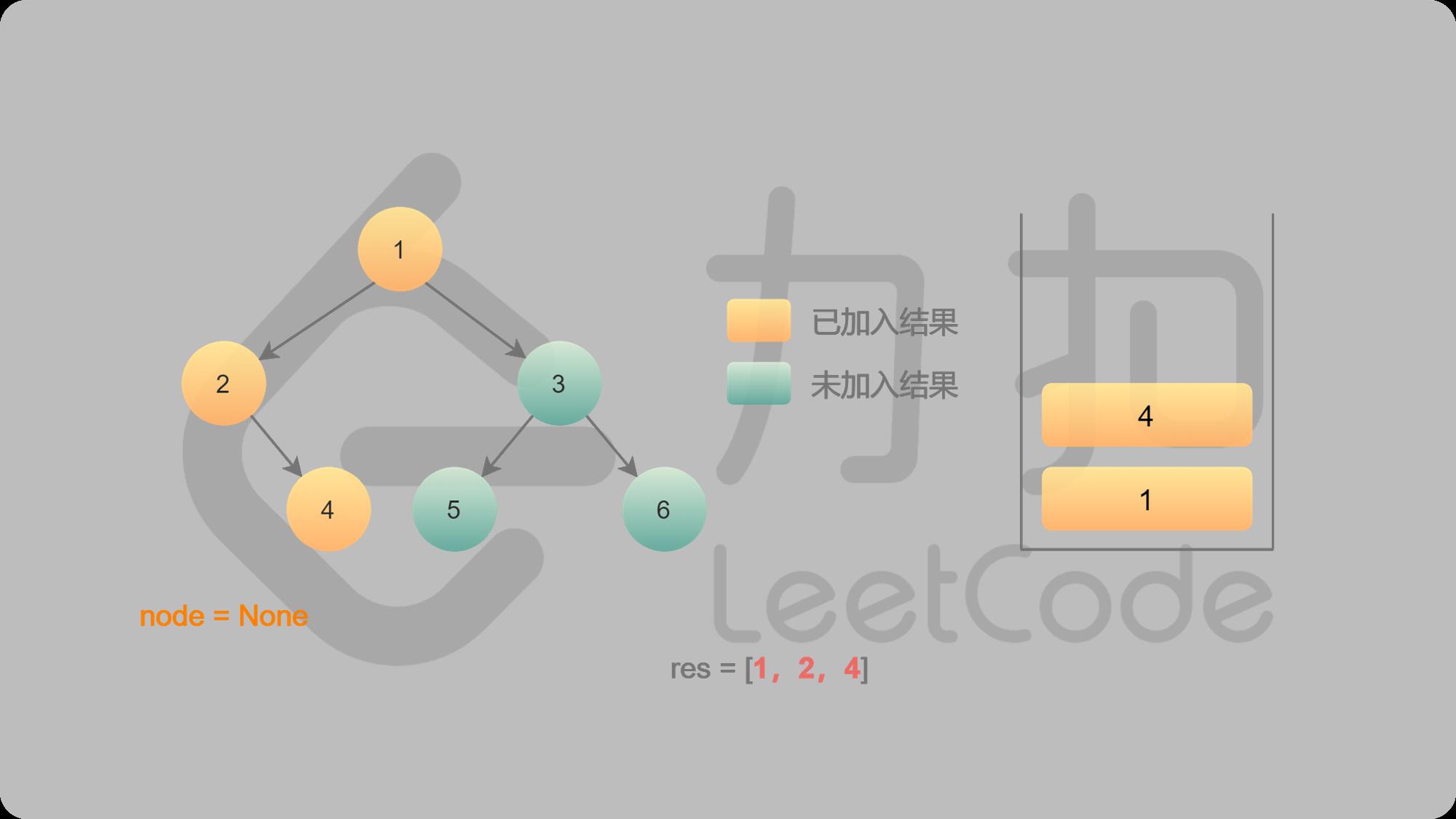
6 4的左子结点不存在,4出栈,然后找4的右子结点,4的右子结点不存在,返回
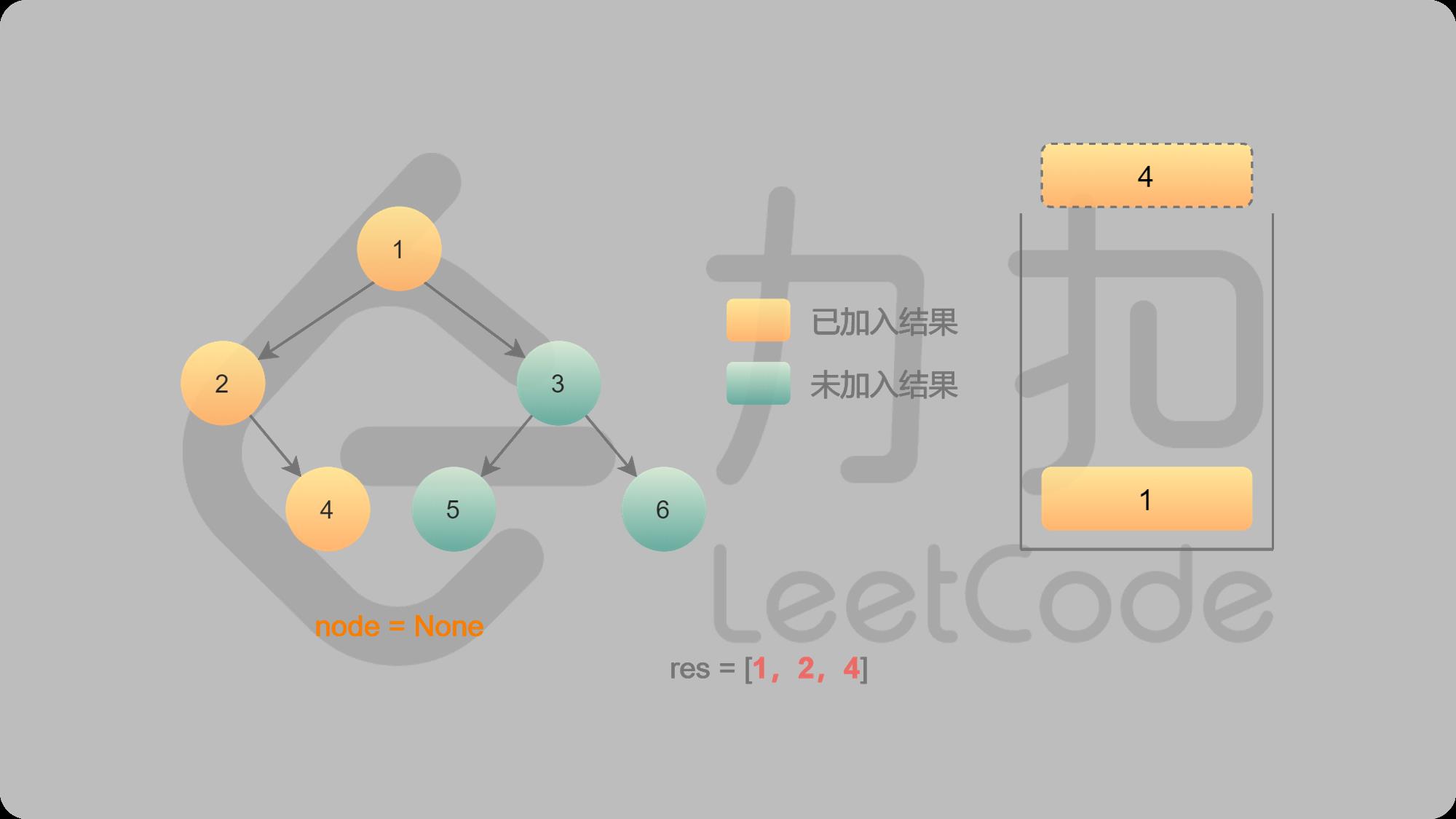
7 1出栈,找1的右子结点3
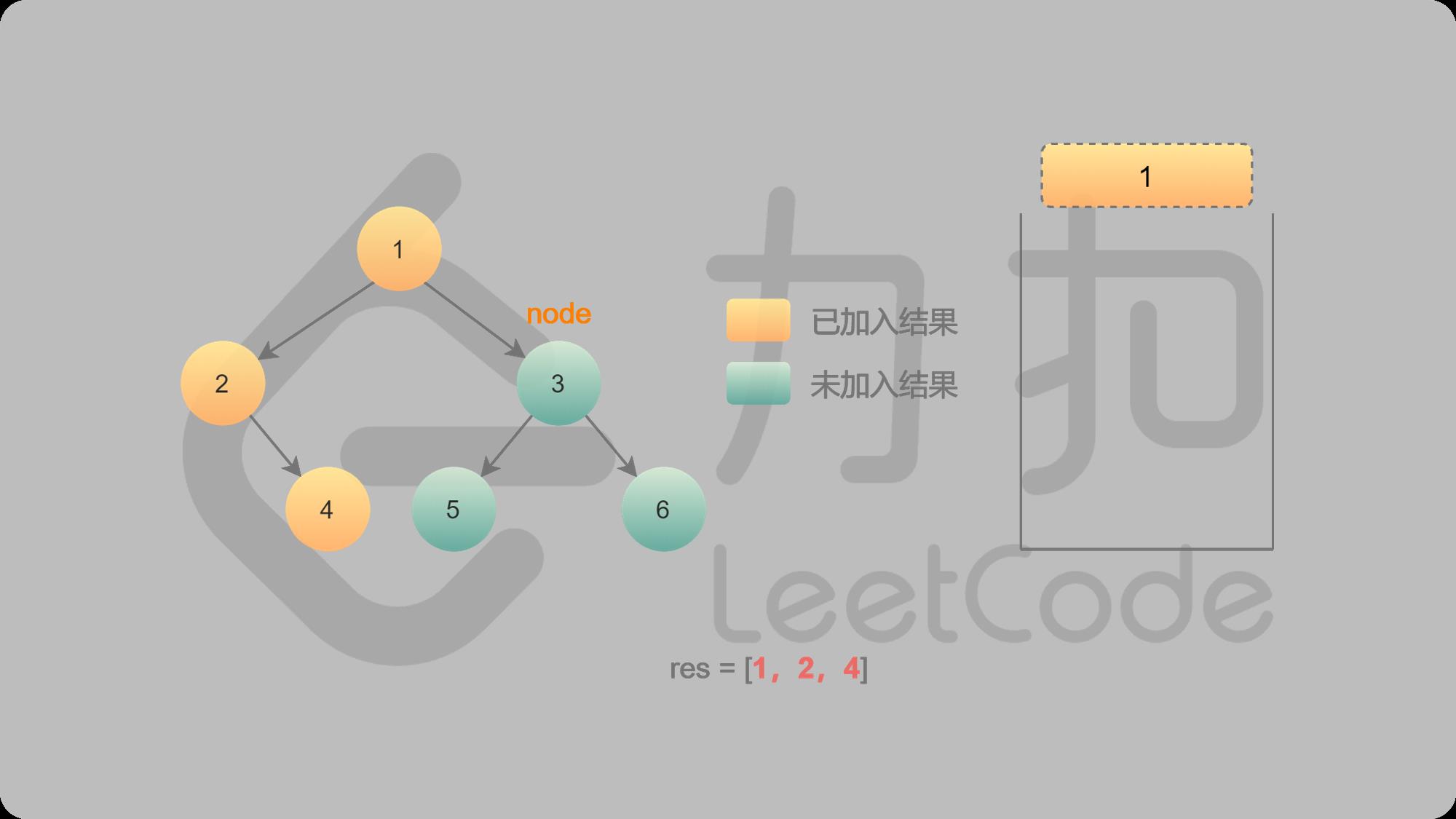
8 3入栈并输出,找3的左子结点5
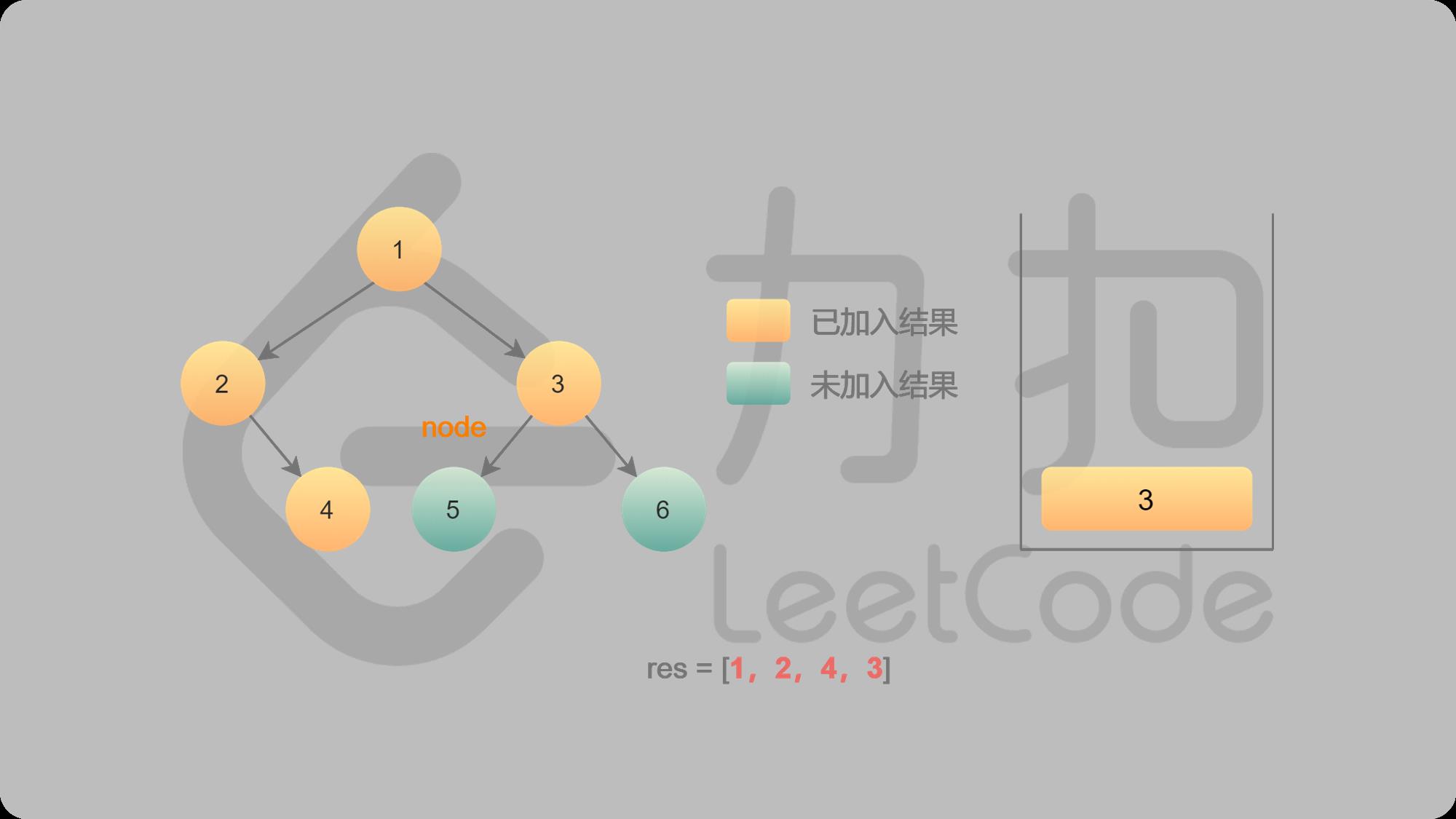
9 5入栈并输出,找5的左子结点,左结点不存在
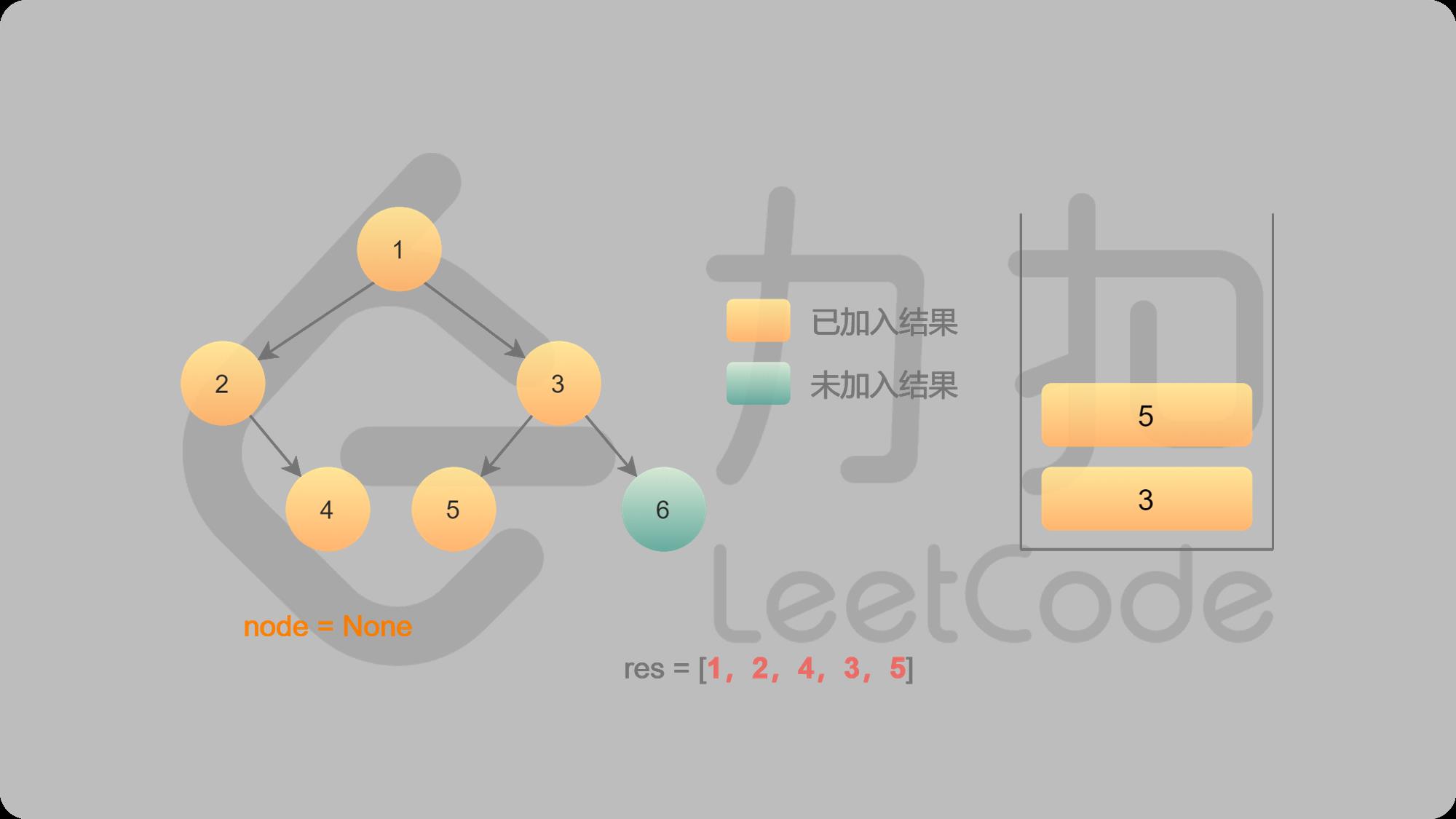
10 5出栈,找5的右子结点,右结点不存在,返回
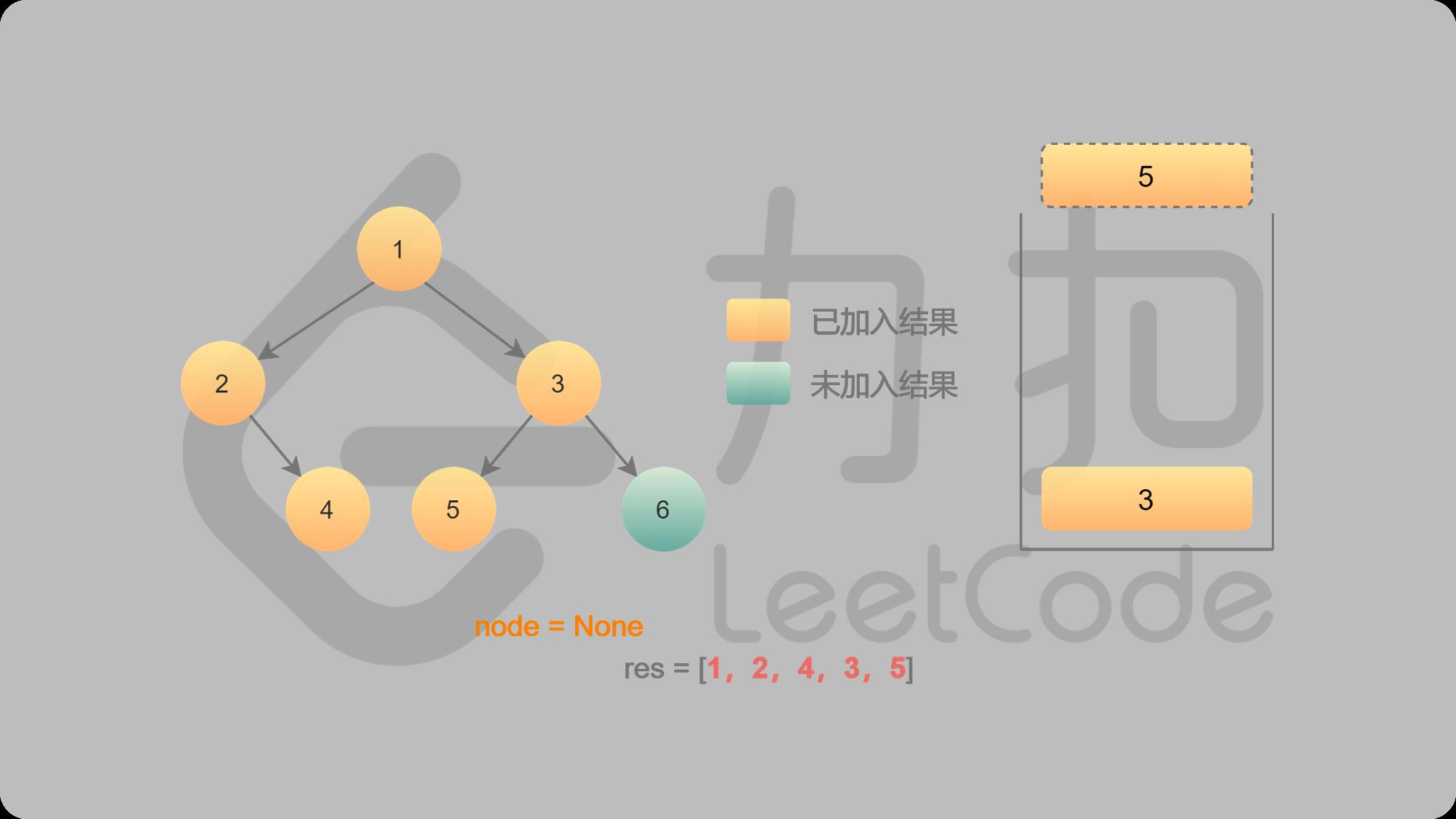
11 3出栈,找3的右子结点6
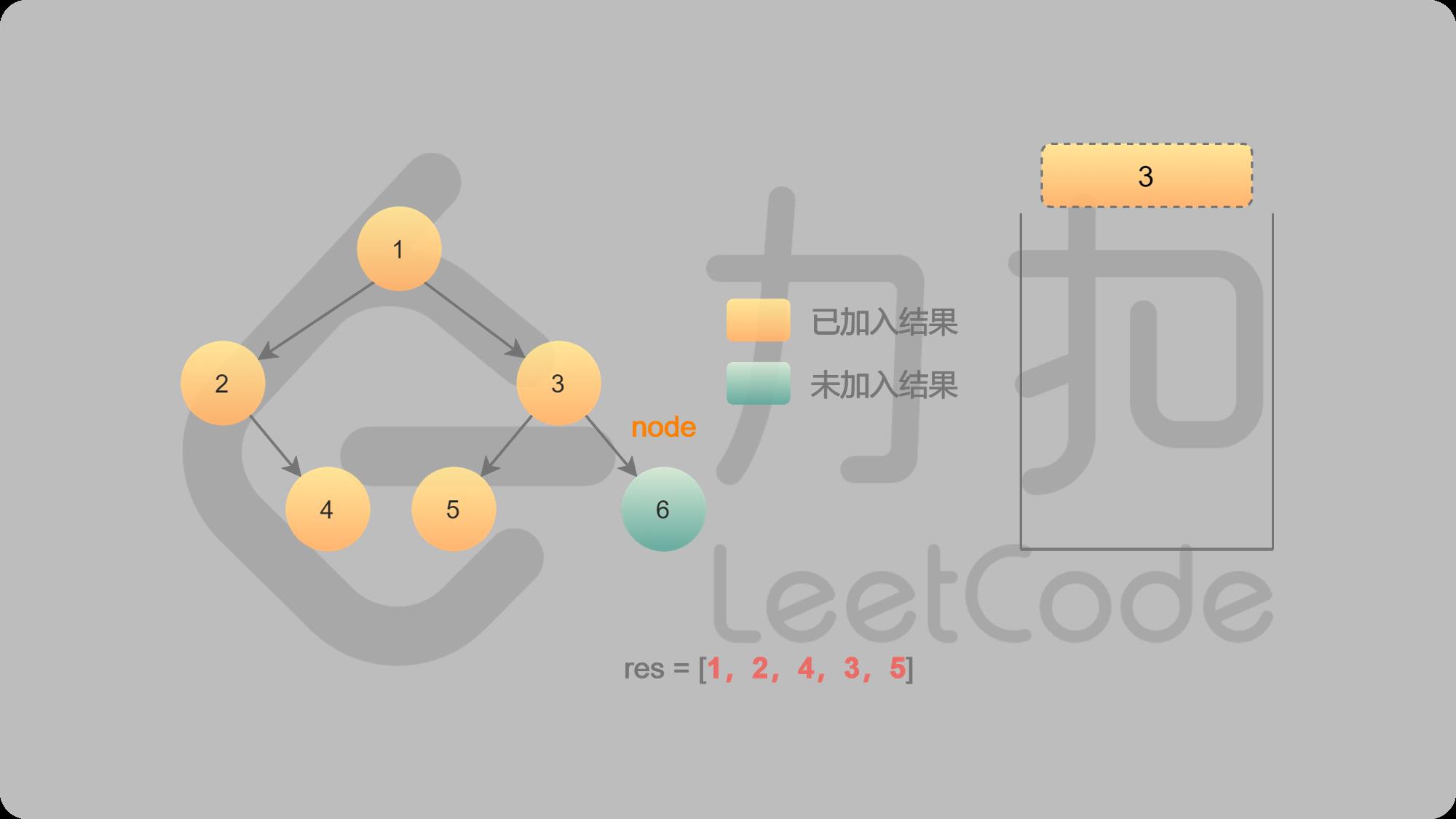
12 6入栈并输出,找6的左子结点,左结点不存在
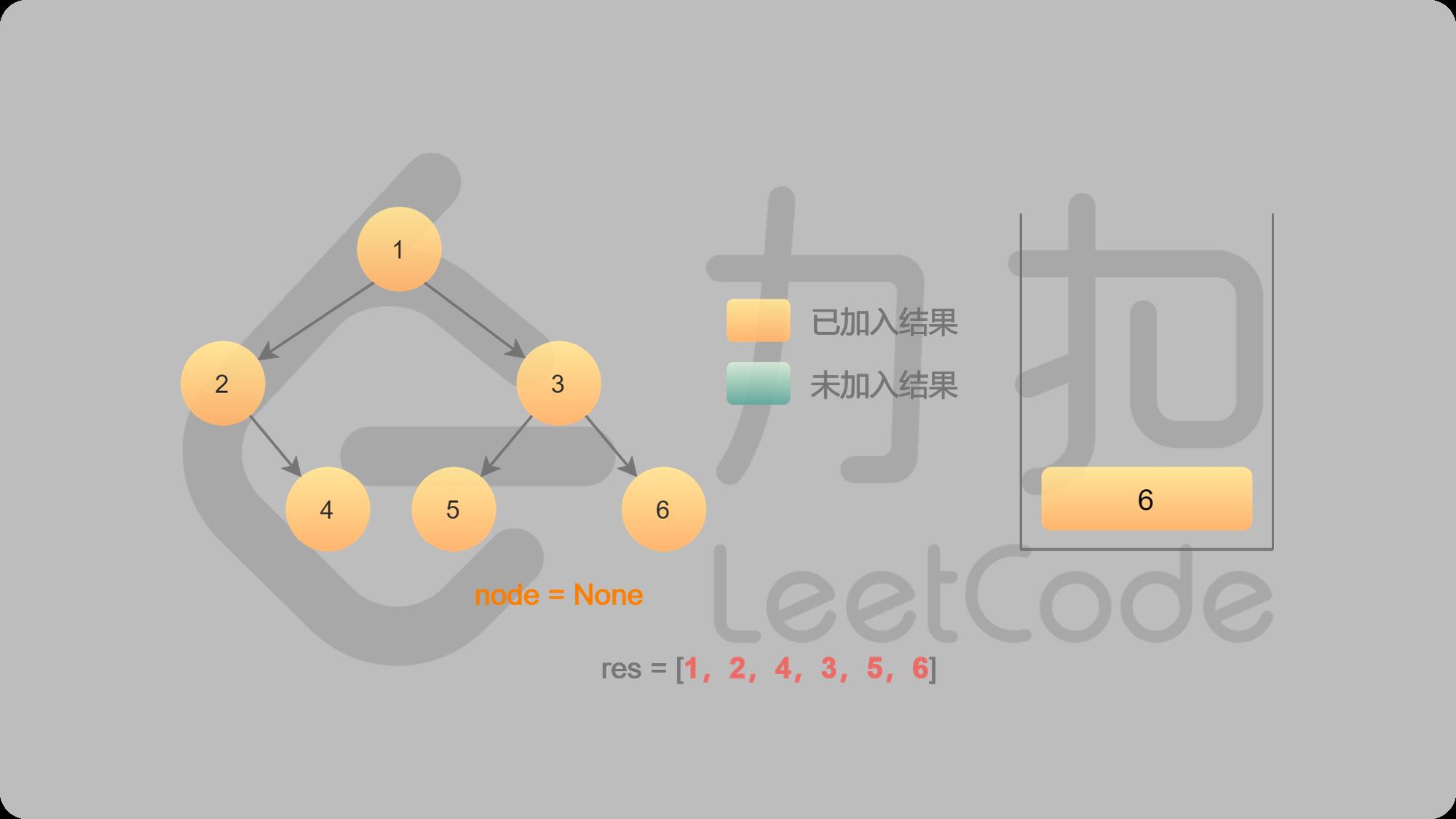
13 6出栈,找6的右子结点,右子结点不存在,返回
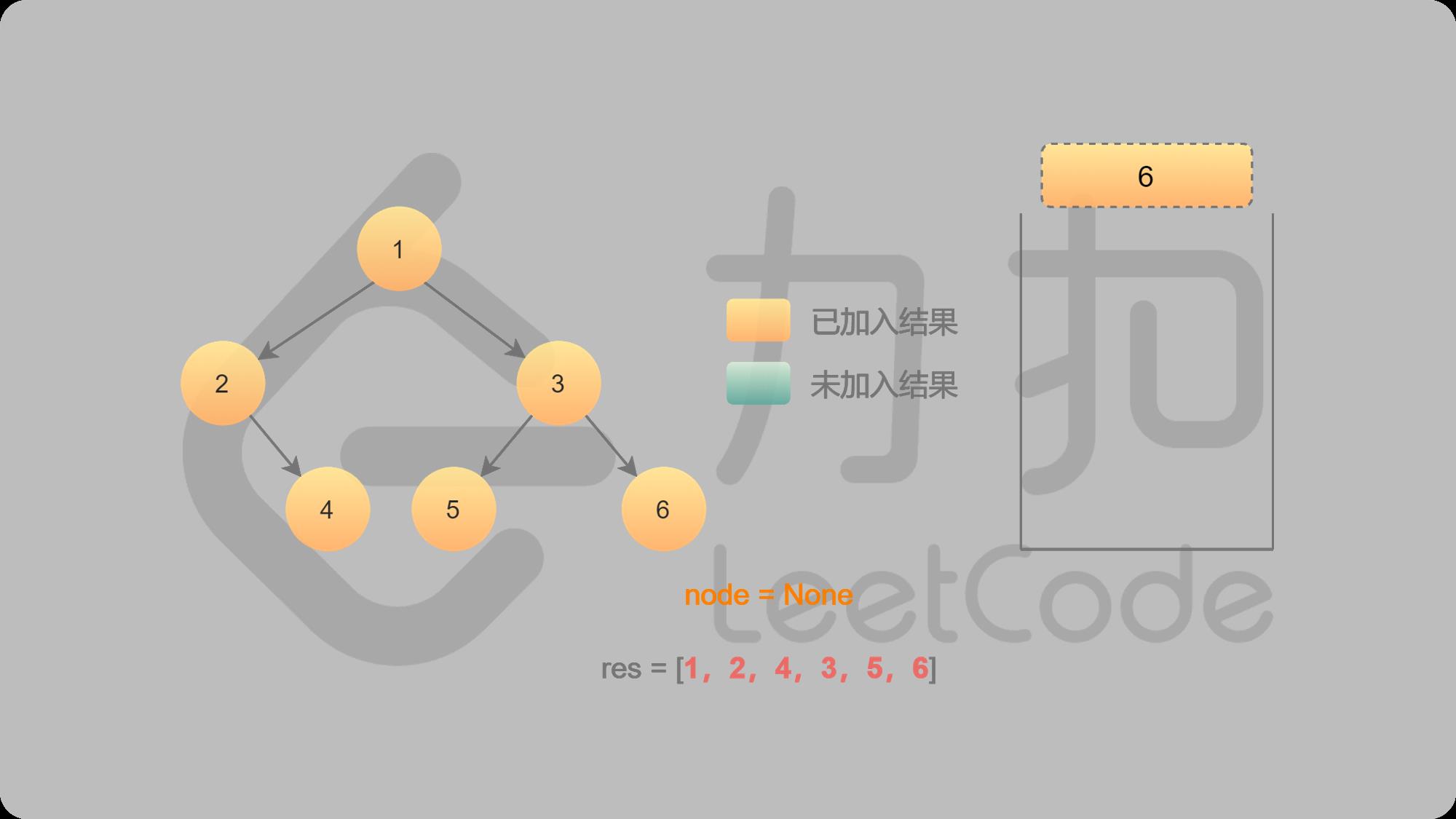
14 完成,栈空
前序遍历代码:
//前序遍历(非递归)
void treePrePrint(Tree tree)
cout << "前序遍历:";
stack<Tree> nodes; //用栈的原因:后进先出,后面进来的结点是下面的,先弹出这个结点,接着找右子结点
while (tree != NULL || !nodes.empty()) //当前结点不为空,或者结点栈不为空,一直循环,说明还有未输出的结点
while (tree != NULL) //只要结点不为空,一直找左子结点
nodes.push(tree);
cout << tree->data << " "; //输出当前结点,前序遍历,先输出根结点
tree = tree->leftchild; //不断找左子结点
//上面循环结束,说明tree结点没有左子树
if (!nodes.empty()) //只要结点队列不为空,就弹出一个结点
tree = nodes.top(); //弹出没有左子树的结点
nodes.pop();
tree = tree->rightchild; //转到这个树的右子结点,继续循环
cout << "\\n";
前序遍历例题
Talk is cheap, Show me the Code.
用下面的例题,趁热打铁练习一下前序遍历
二叉树的中序遍历(非递归)
递归方法代码里面有注释
中序遍历和前序遍历是差不多的
中序遍历:先输出左结点,在输出根结点,在输出右结点
使用栈,栈后进先出,从根结点向下添加,先把下面的输出,然后在一步一步向上走
先把根结点添加,
结点压栈,找此结点的左子树,重复这个操作一直找到左子树为空的时候
然后从栈里弹出结点,此时弹出的结点为上面最后一个左子树为空的结点(栈后进先 出),输出此结点
使用弹出结点的右结点循环上面的操作,
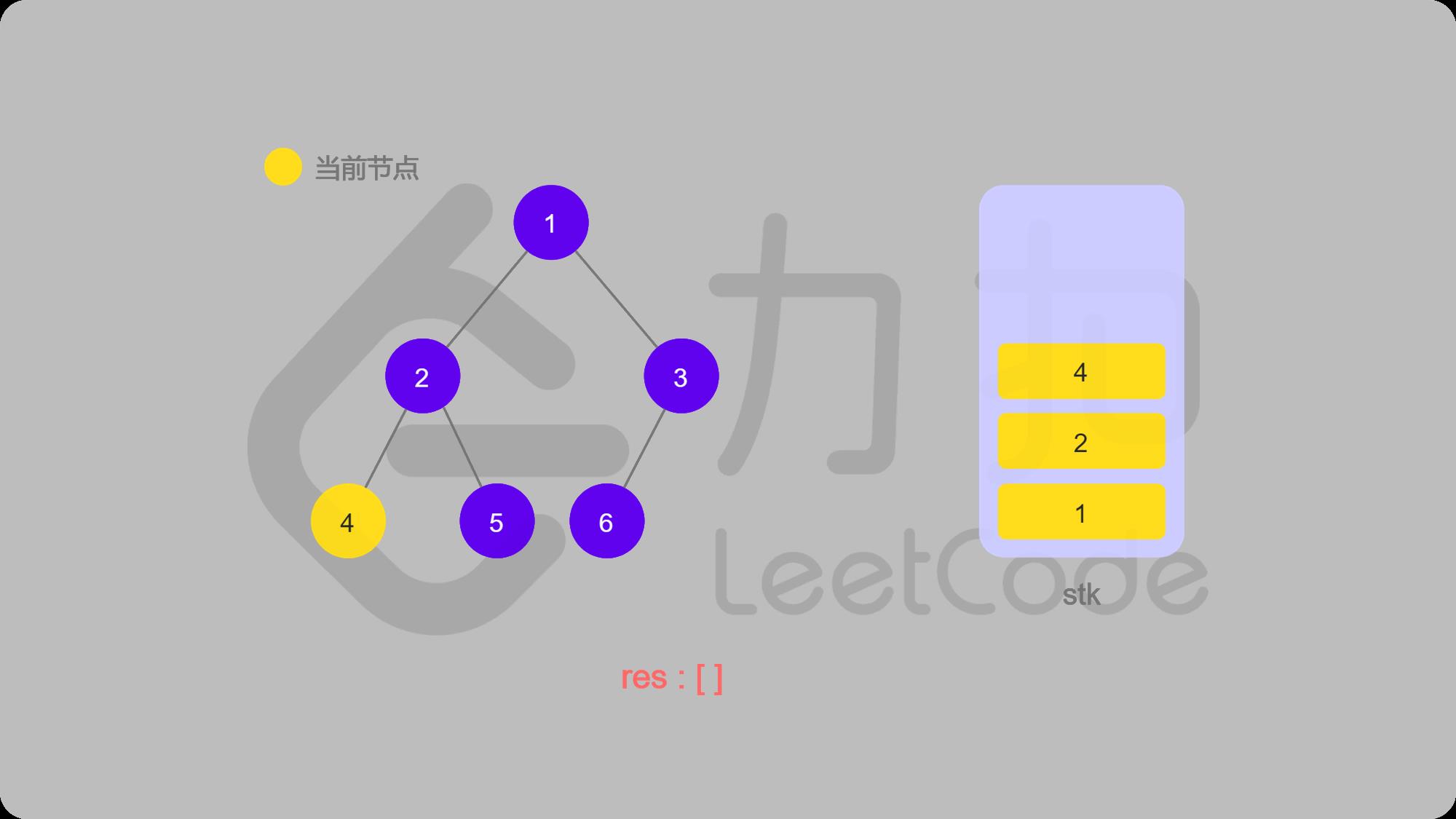
LeetCode二叉树中序遍历图解:
1 初始状态
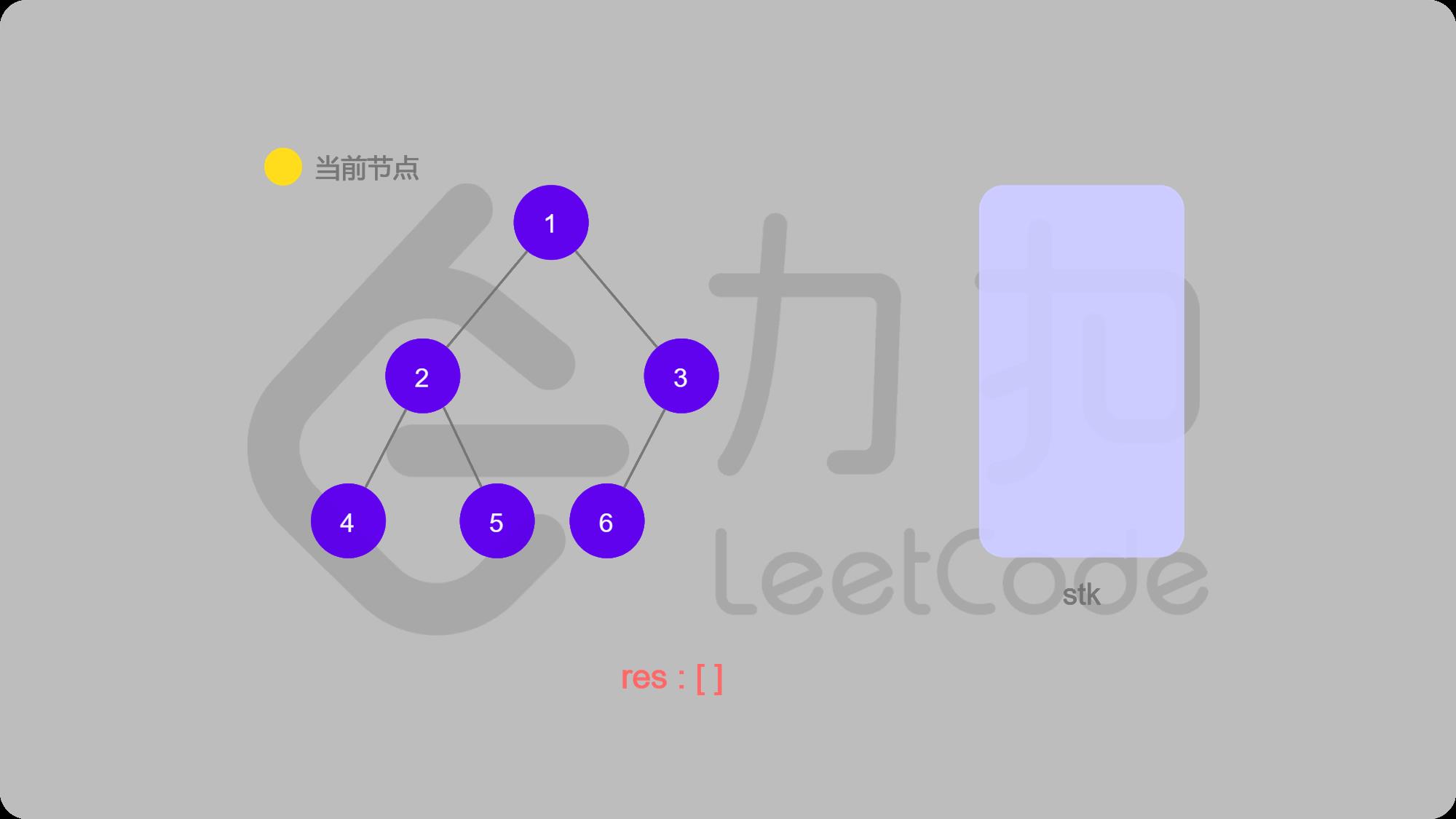
2 1入栈,然后找左子结点2
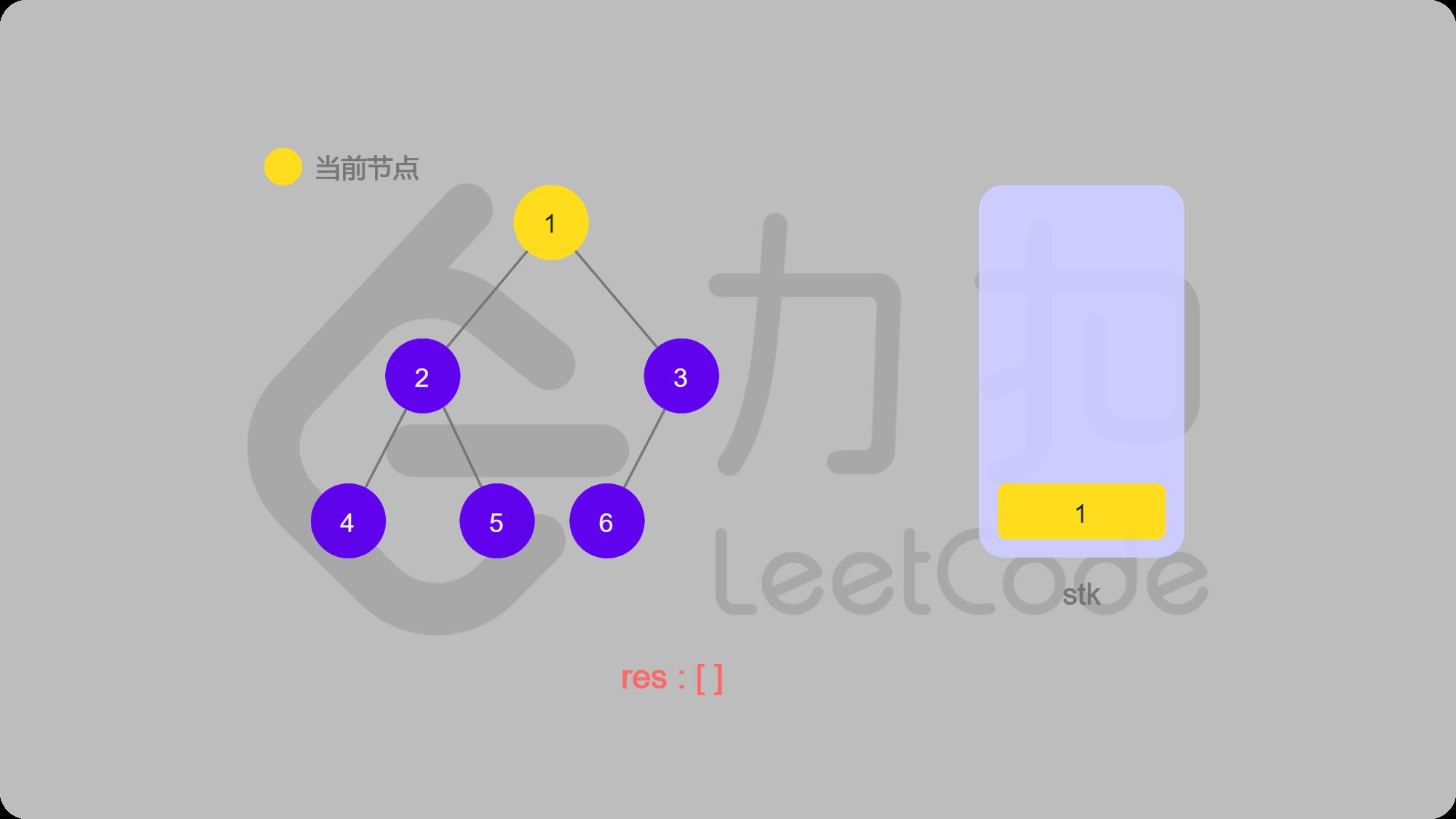
3 2入栈,然后找左子结点4
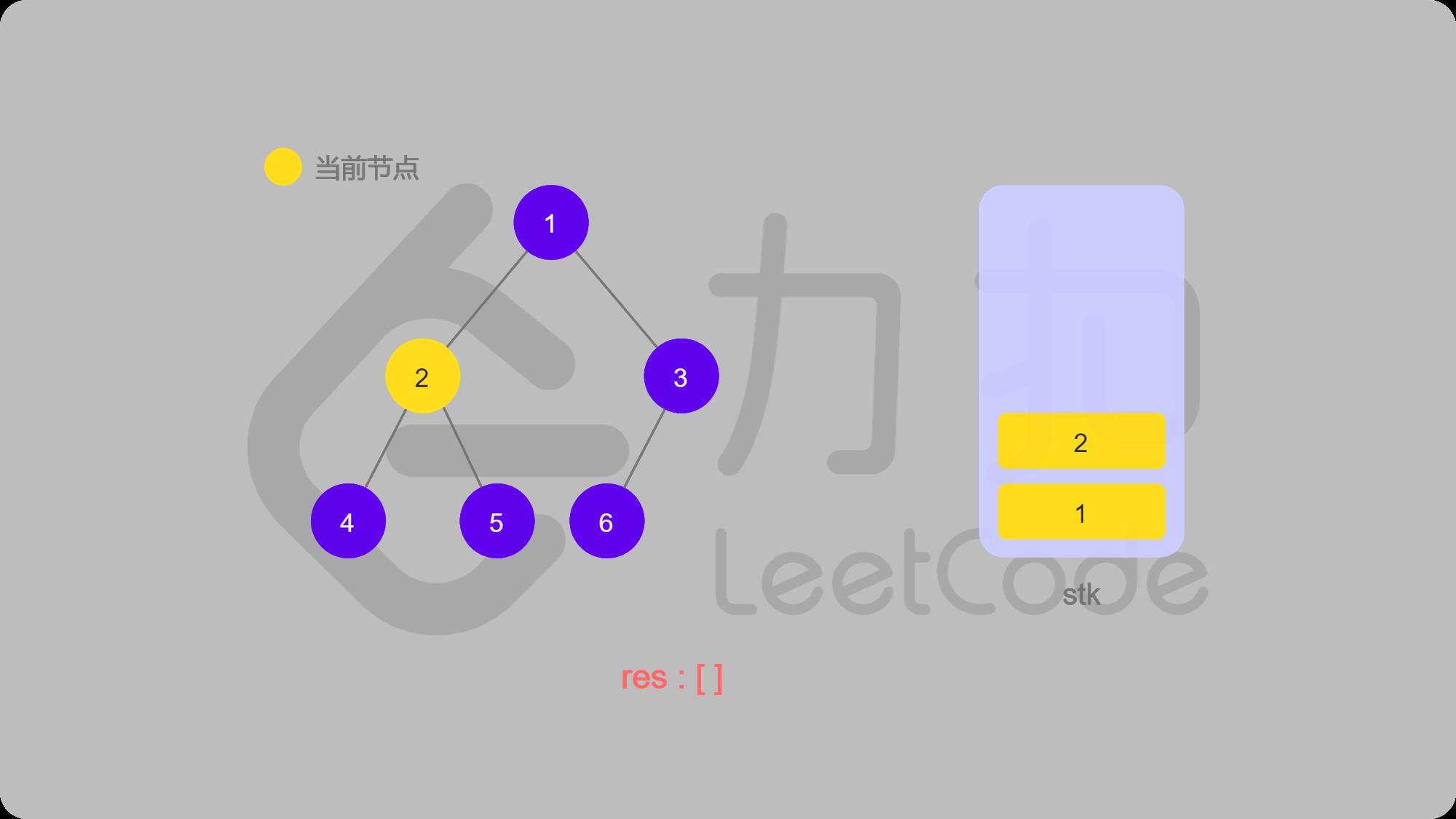
4 4入栈然后找左子结点,4没有左子结点
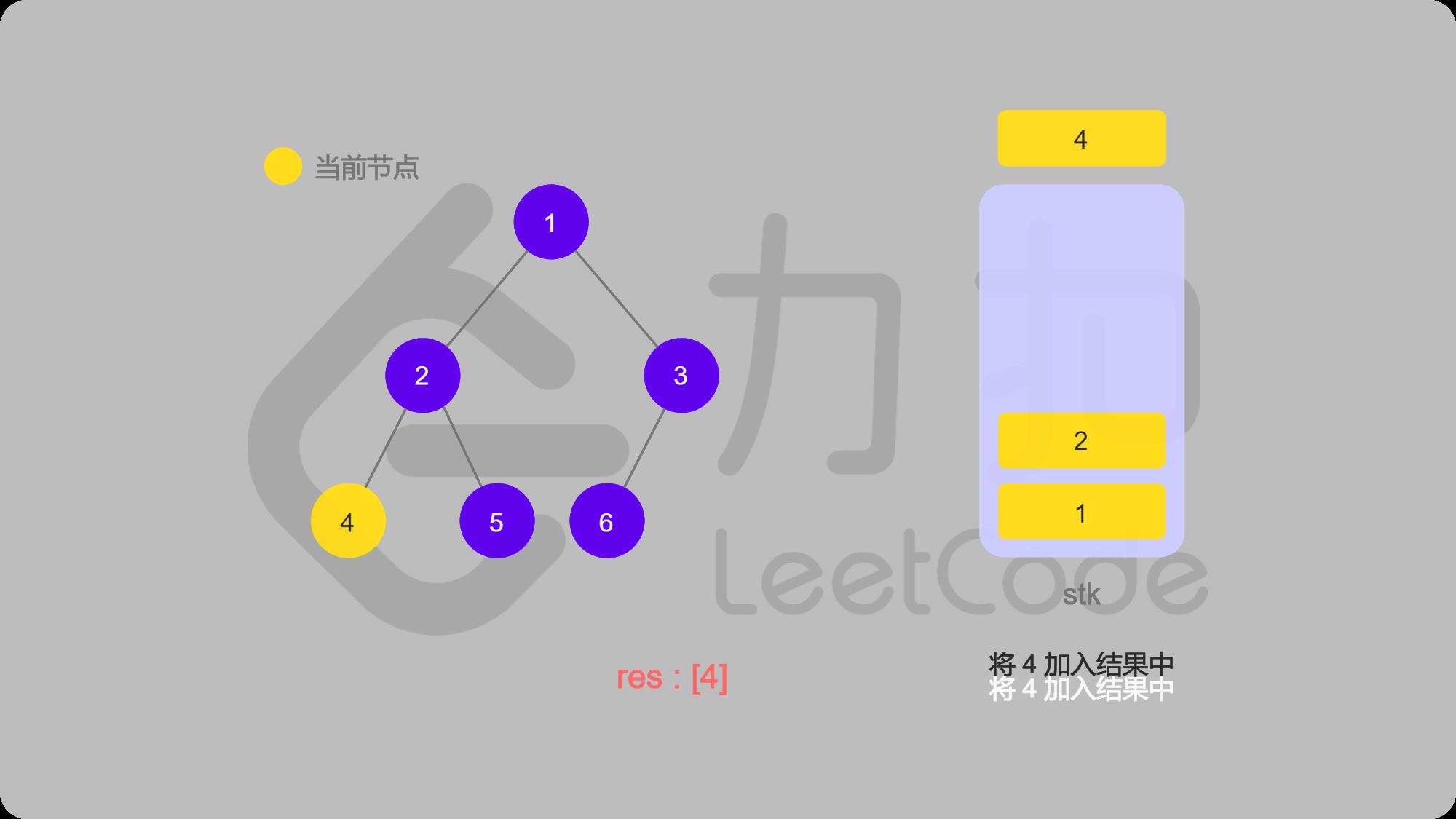
5 4出栈并输出,然后找右子结点,右子结点不存在,返回
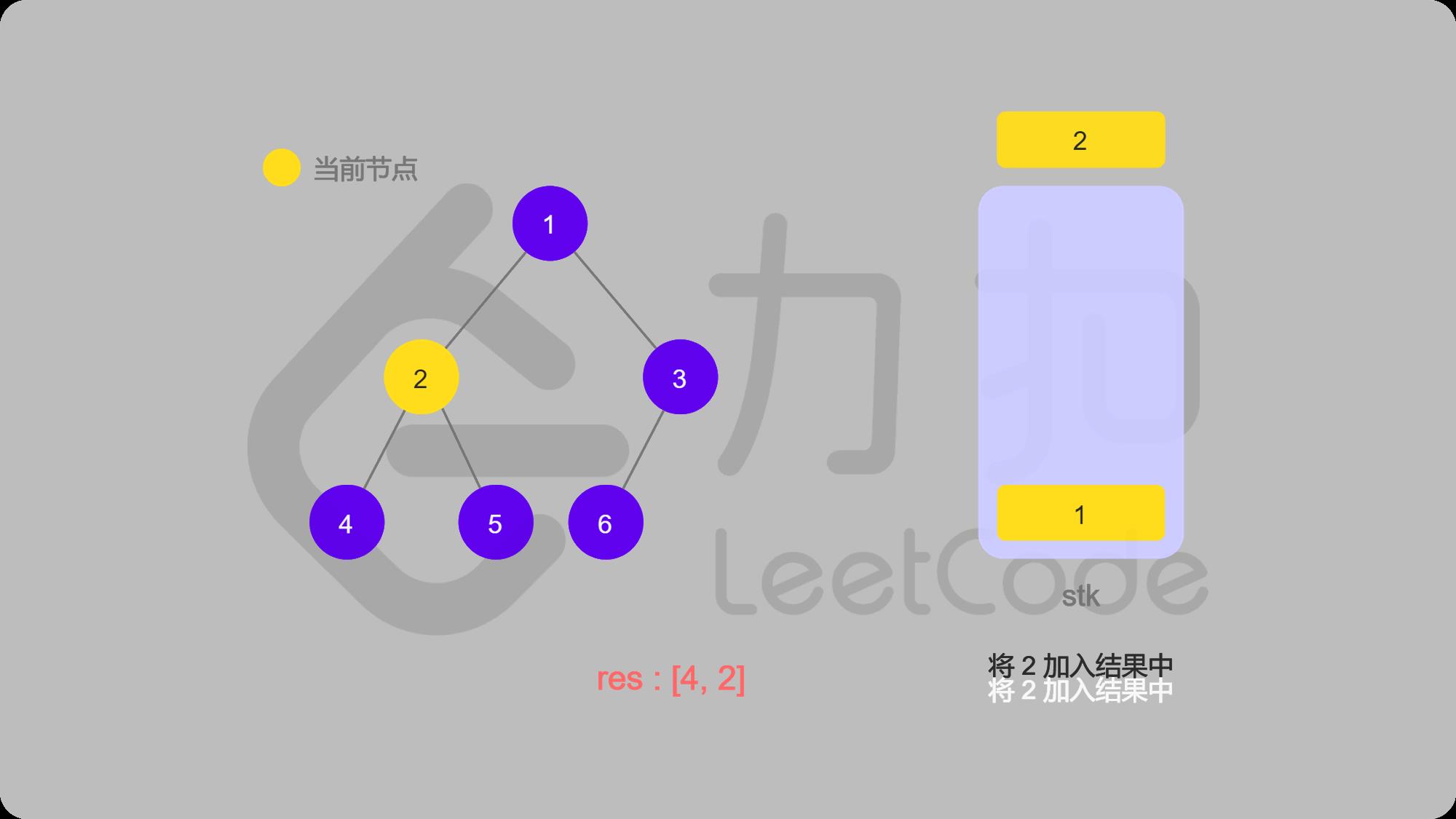
6 2出栈并输出,找2的右子结点5
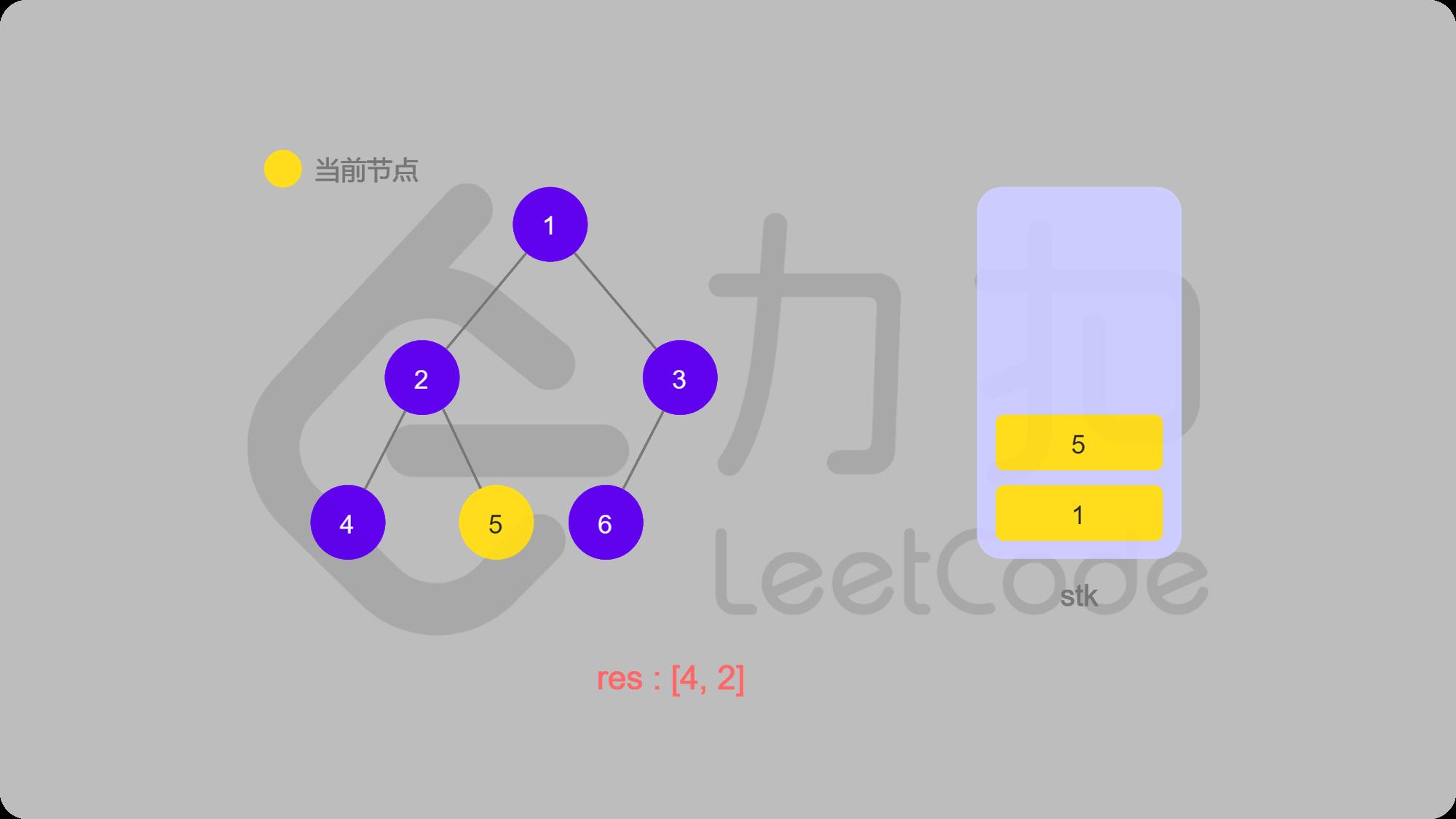
7 5入栈,然后找5的左子结点,左结点不存在
8 5出栈并输出,然后找5的右子结点,右结点不存在,返回
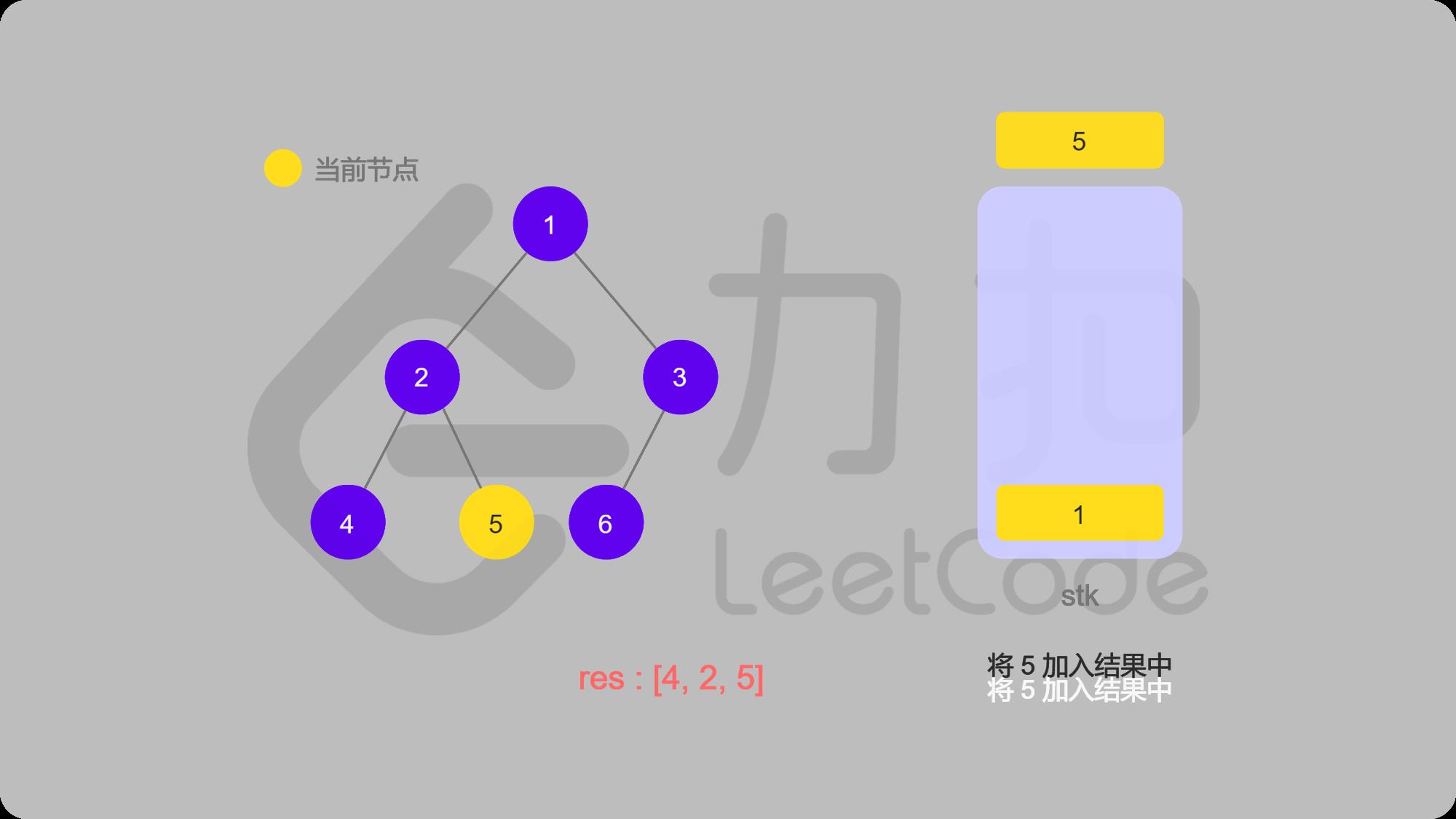
9 1出栈并输出,找1的右子结点3
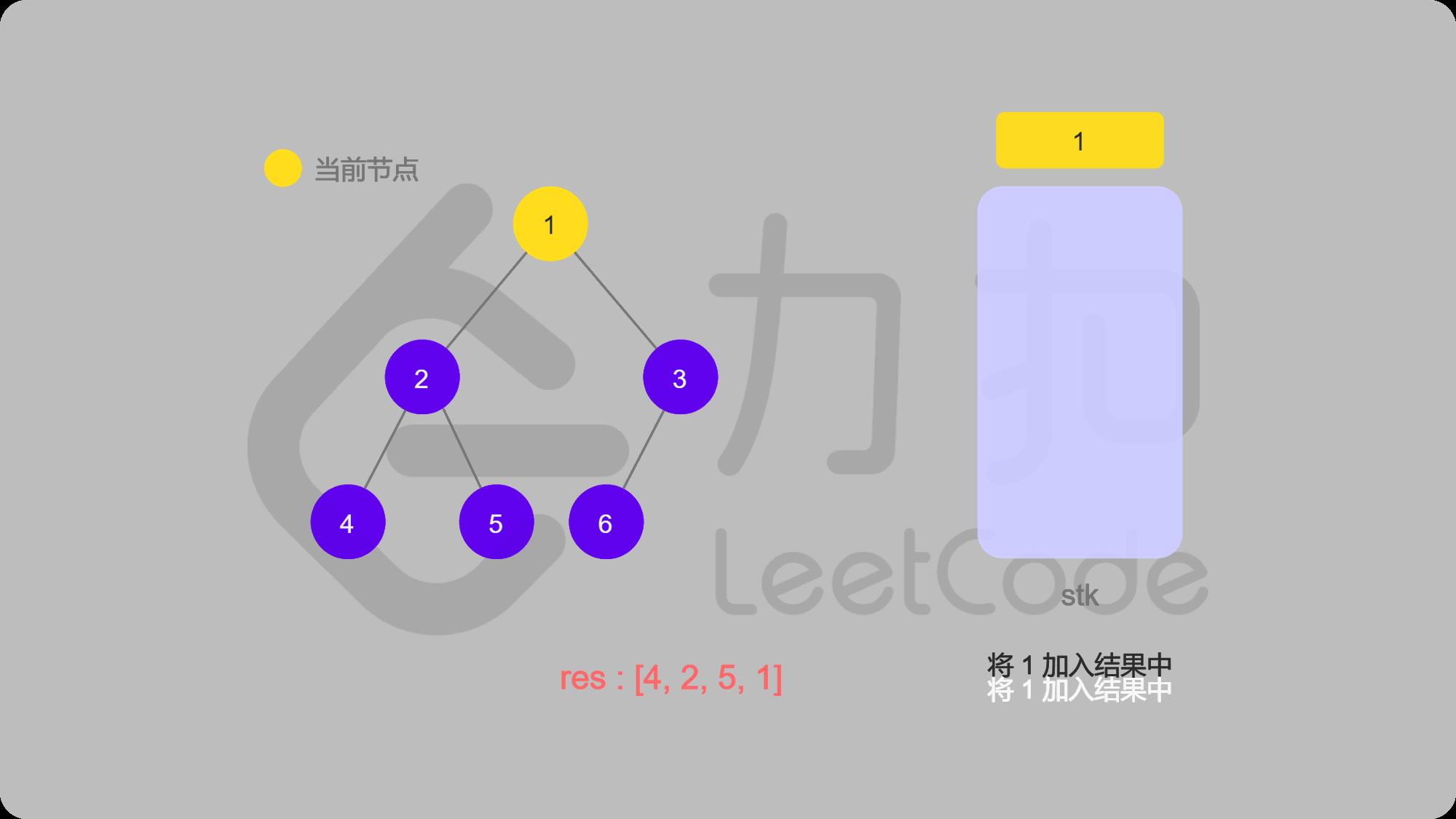
10 3入栈,找3的左子结点
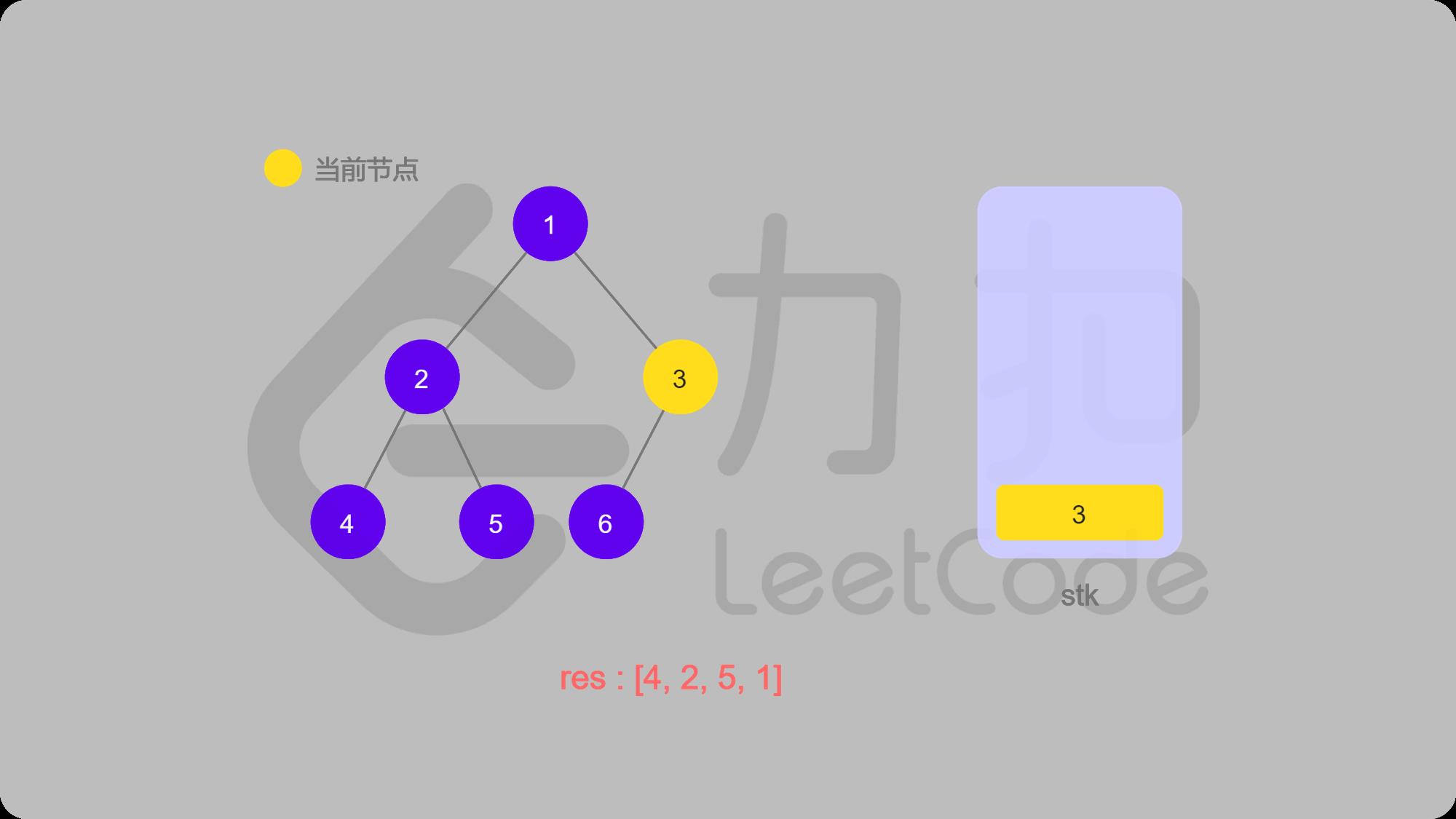
11 6入栈,找6的左子结点,6的左子结点为空
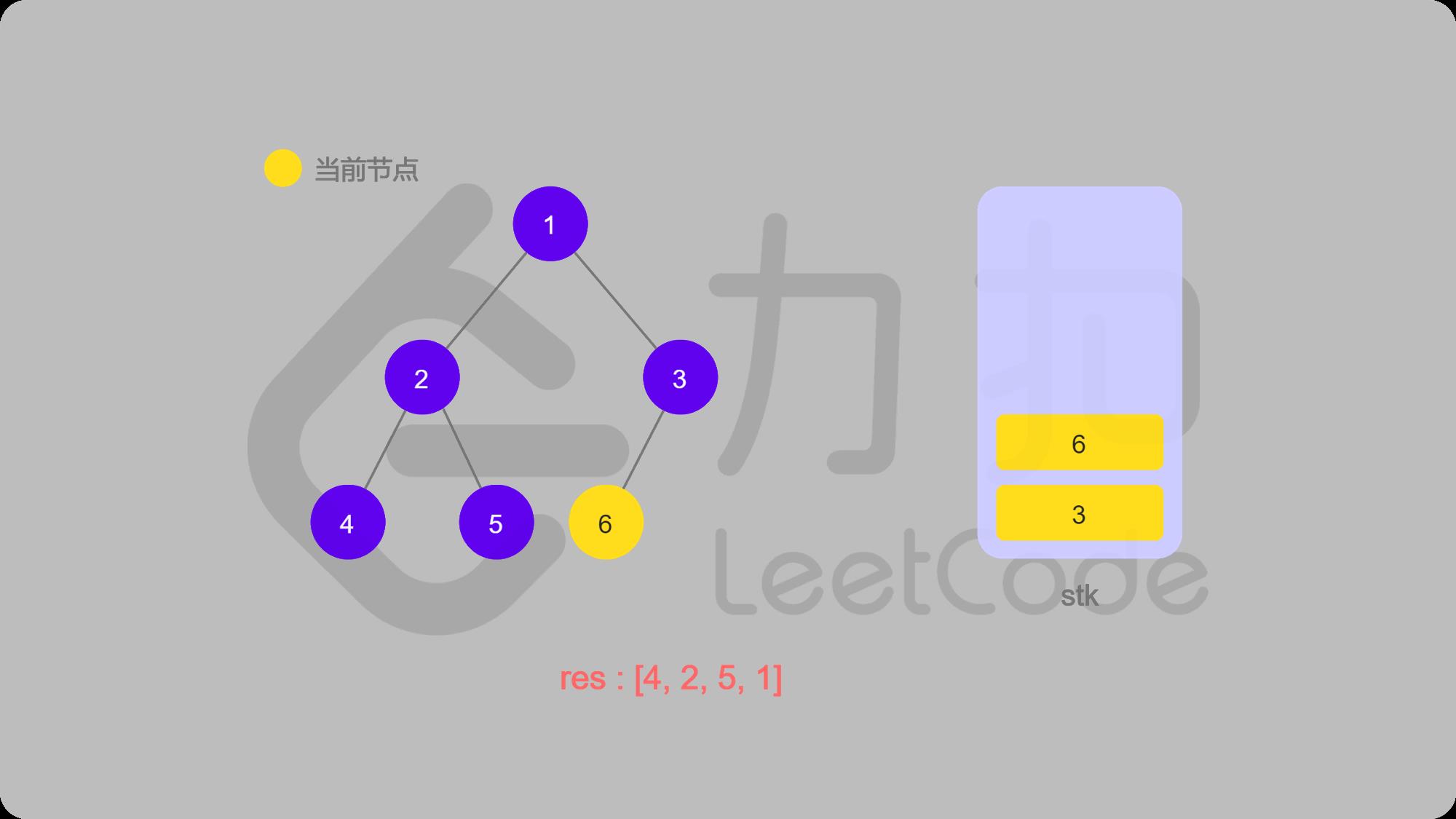
12 6出栈并输出,找6的右子结点,右子结点为空,返回
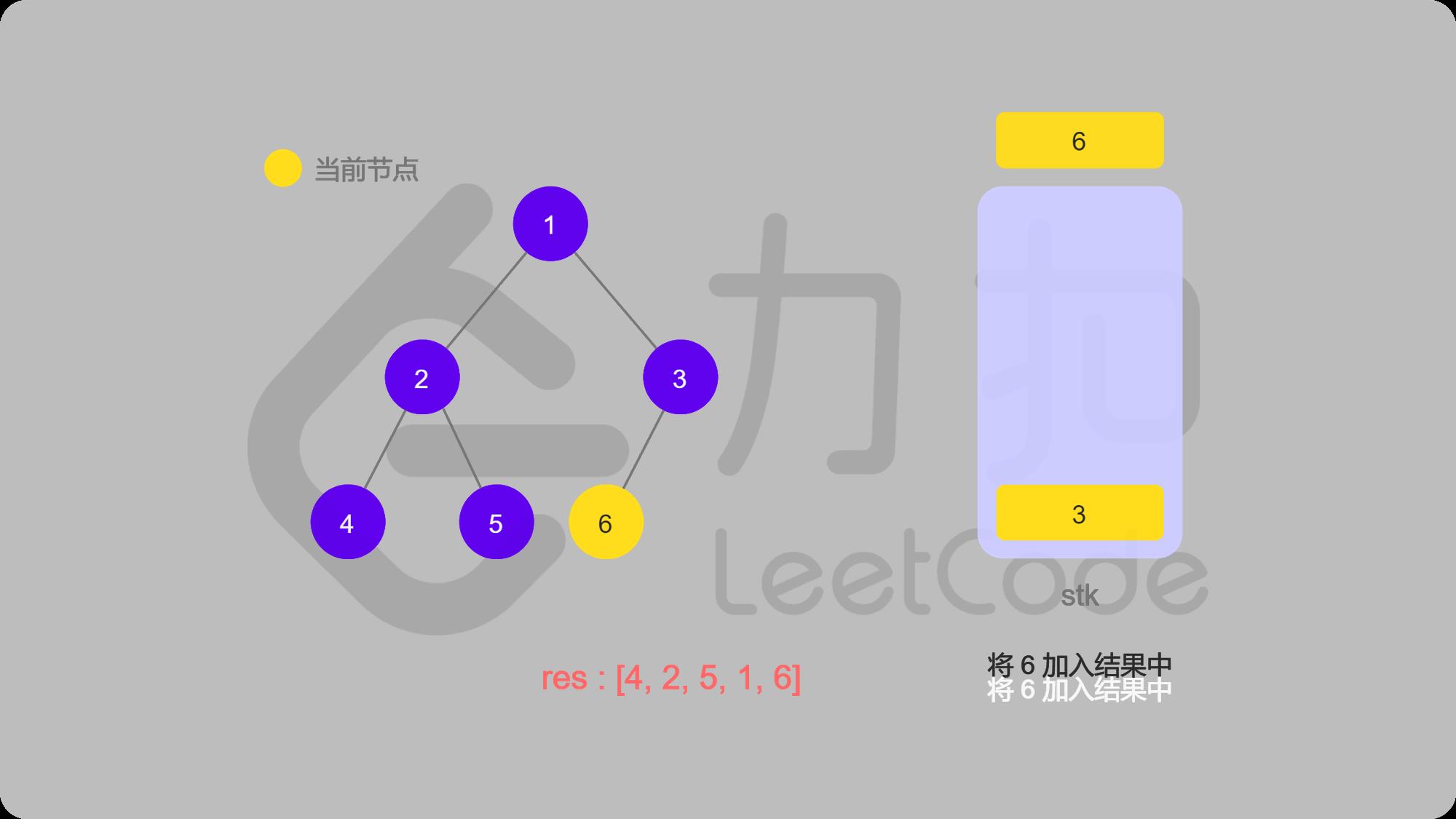
13 3出栈并输出,找3的右子结点,右结点为空,返回
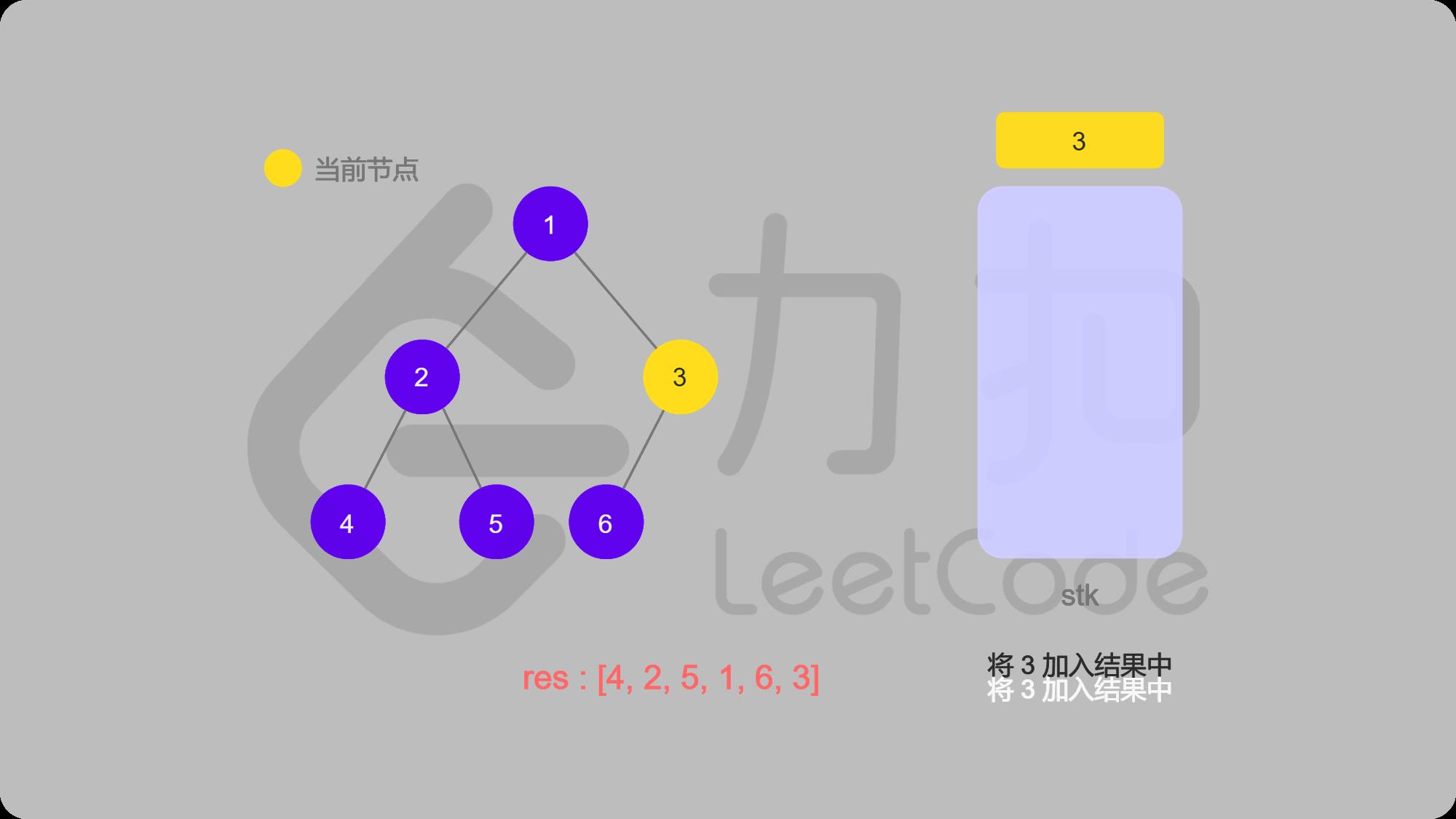
14 中序遍历完成
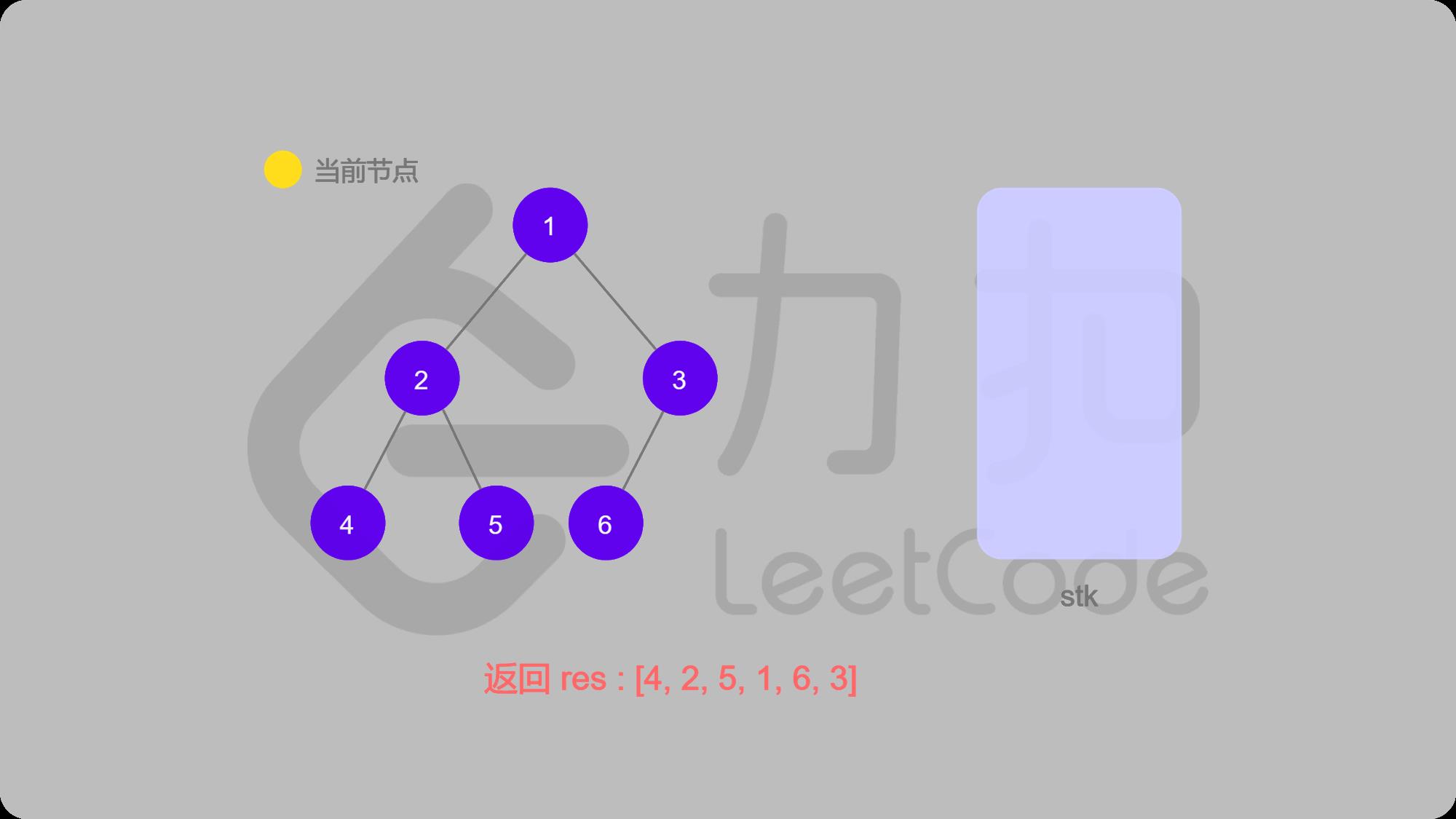
中序遍历代码:
//中序遍历(非递归)
void treeMidPrint(Tree tree) //与前序遍历大概相同,不过是先输出左子结点
cout << "中序遍历:";
stack<Tree> nodes;
while (tree != NULL || !nodes.empty())
while (tree != NULL)
nodes.push(tree);
tree = tree->leftchild;
//当左子结点遍历完后,输出根结点,然后再转到右结点
if (!nodes.empty())
tree = nodes.top();
nodes.pop();
cout << tree->data << " ";
tree = tree->rightchild;
cout << "\\n";
中序遍历例题
Talk is cheap, Show me the Code.
用下面的例题,趁热打铁练习一下中序遍历
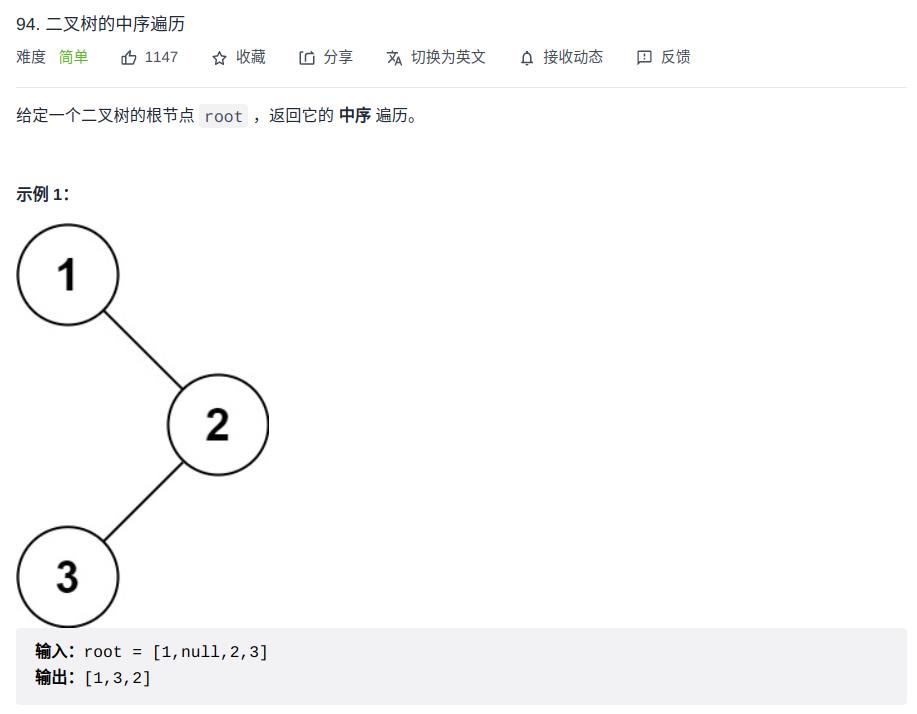
二叉树的后序遍历(非递归)
递归方法代码里面有注释
后序遍历:先输出左结点,在输出右结点,在输出根结点
因为后序遍历是最后输出根结点,我们按照左结点压栈,左结点可以到底,但是还要先访问右结点,才能输出根结点,
所以要找一个变量存一下右结点是否被访问(换句话说,存一下上次访问的结点),
如果右结点被访问了,此时可以输出根结点
使用栈,栈后进先出,从根结点向下添加,先把下面的输出,然后在一步一步向上走
先把根结点添加,
步骤:
结点压栈,找此结点的左子树,重复这个操作一直找到左子树为空的时候
然后从栈里得到栈顶的结点(栈顶未出栈),此时拿到的结点为上面最后一个左子树为空的结点(栈后进先出),
判断一下右结点是否为空或者 上次被访问的是否为右结点(被访问)
如果右结点为空或者被访问:左右结点都被访问了,可以输出根结点,把上次访问的结点改为当前根结点,当前根结点被访问了
如果右结点不为空并且没有被访问:那么把当前结点改为右结点,
使用弹出结点的右结点循环上面的操作,
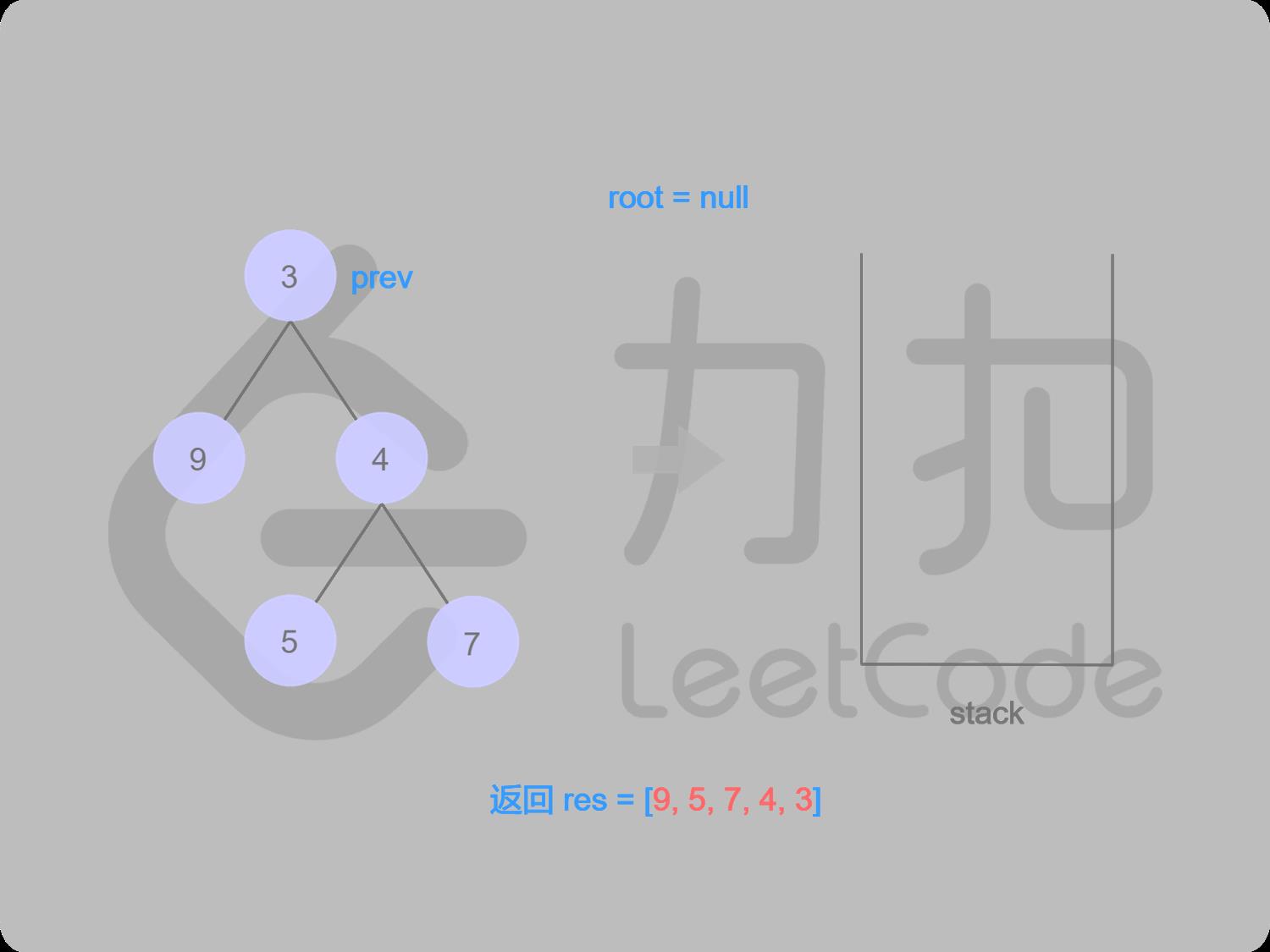
LeetCode二叉树后序遍历图解:
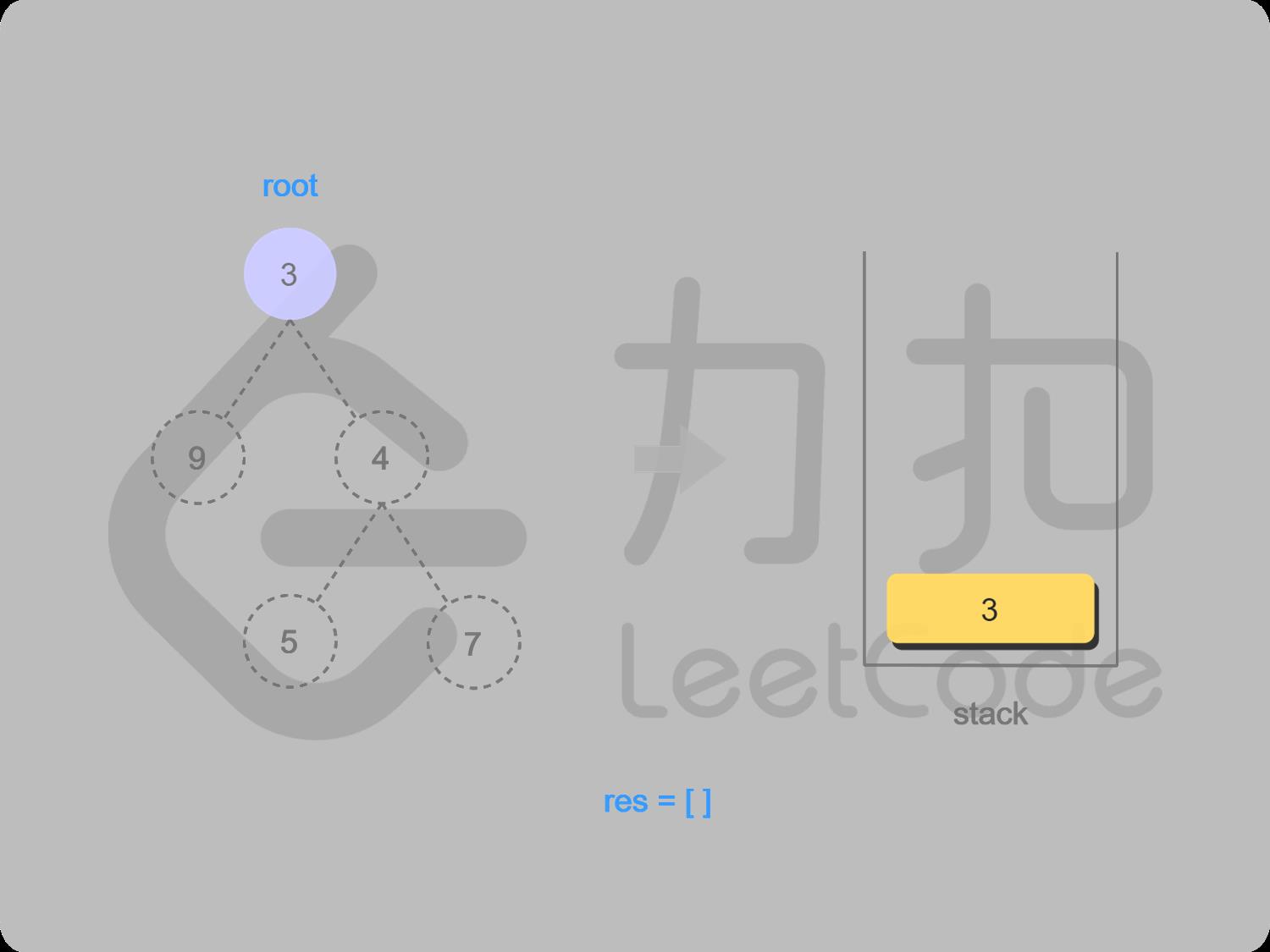
1 初始状态

2 3入栈,找3的左子结点9
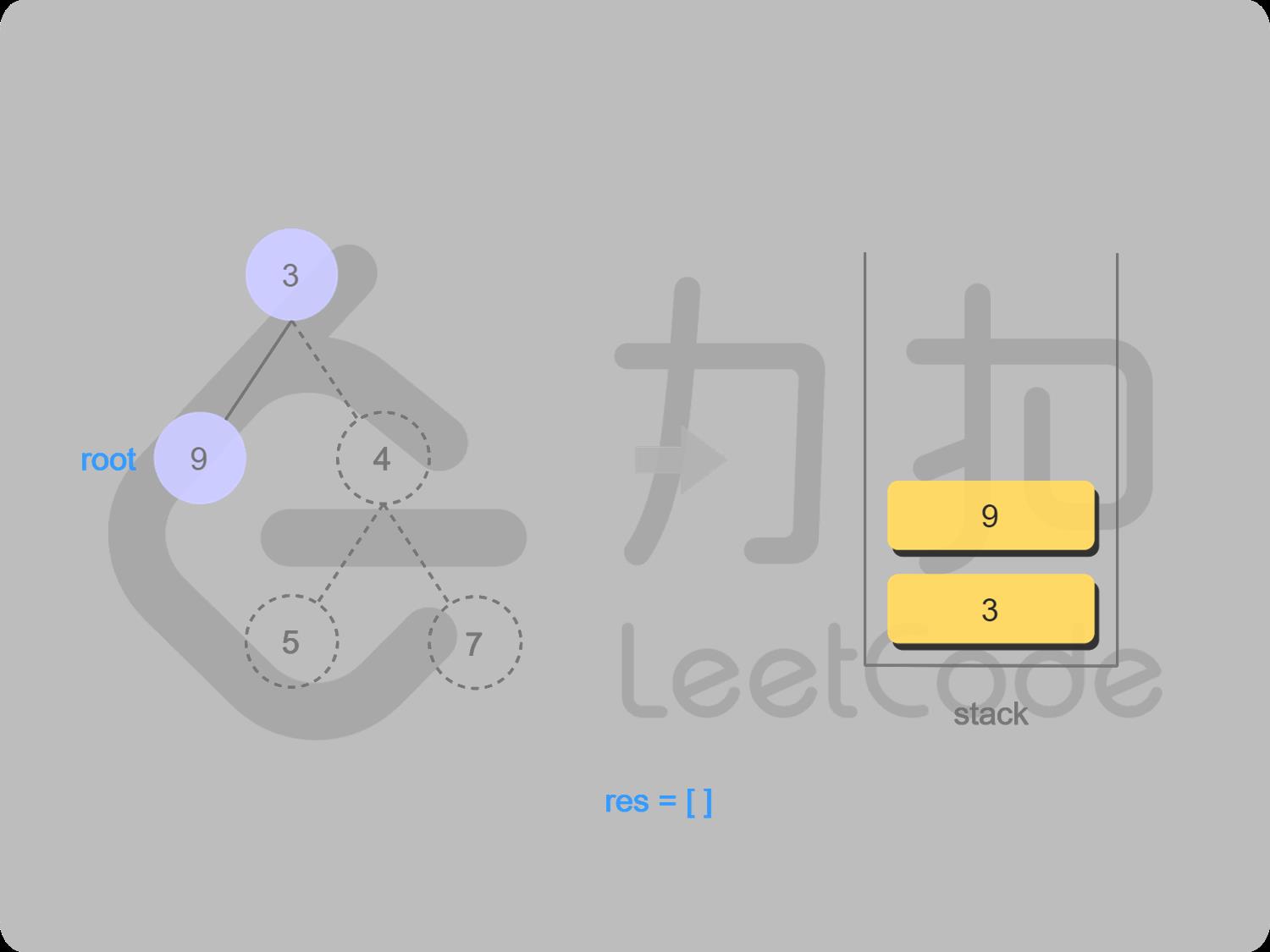
3 9入栈,找9的左子结点,左结点为空
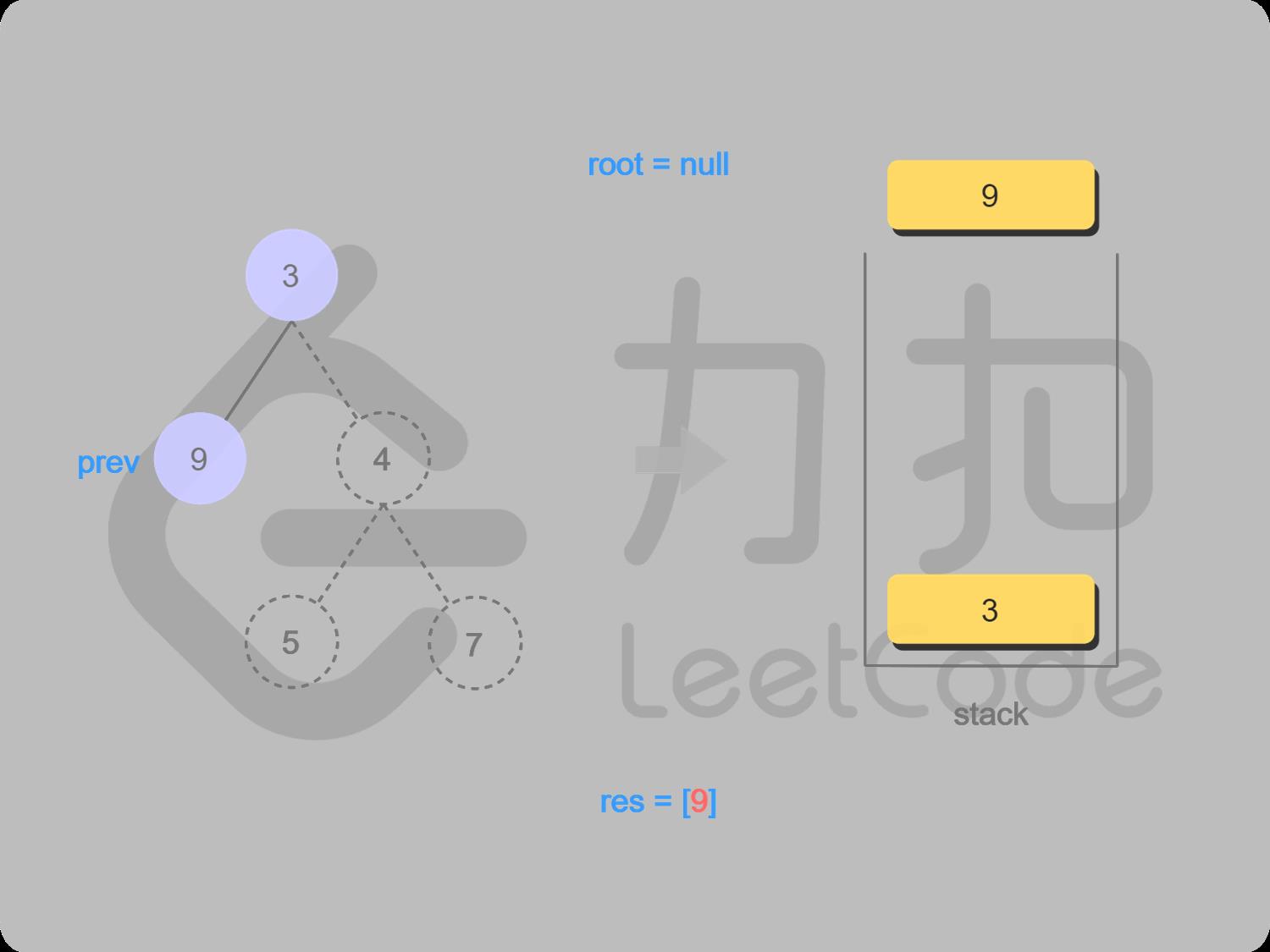
4 取栈顶值9(不出栈),找9的右结点,右结点为空,9的左结点访问过,右结点为空,9出栈并输出,9成为访问过的上一个结点,返回
5 取栈顶值3(不出栈), 找3的右结点,
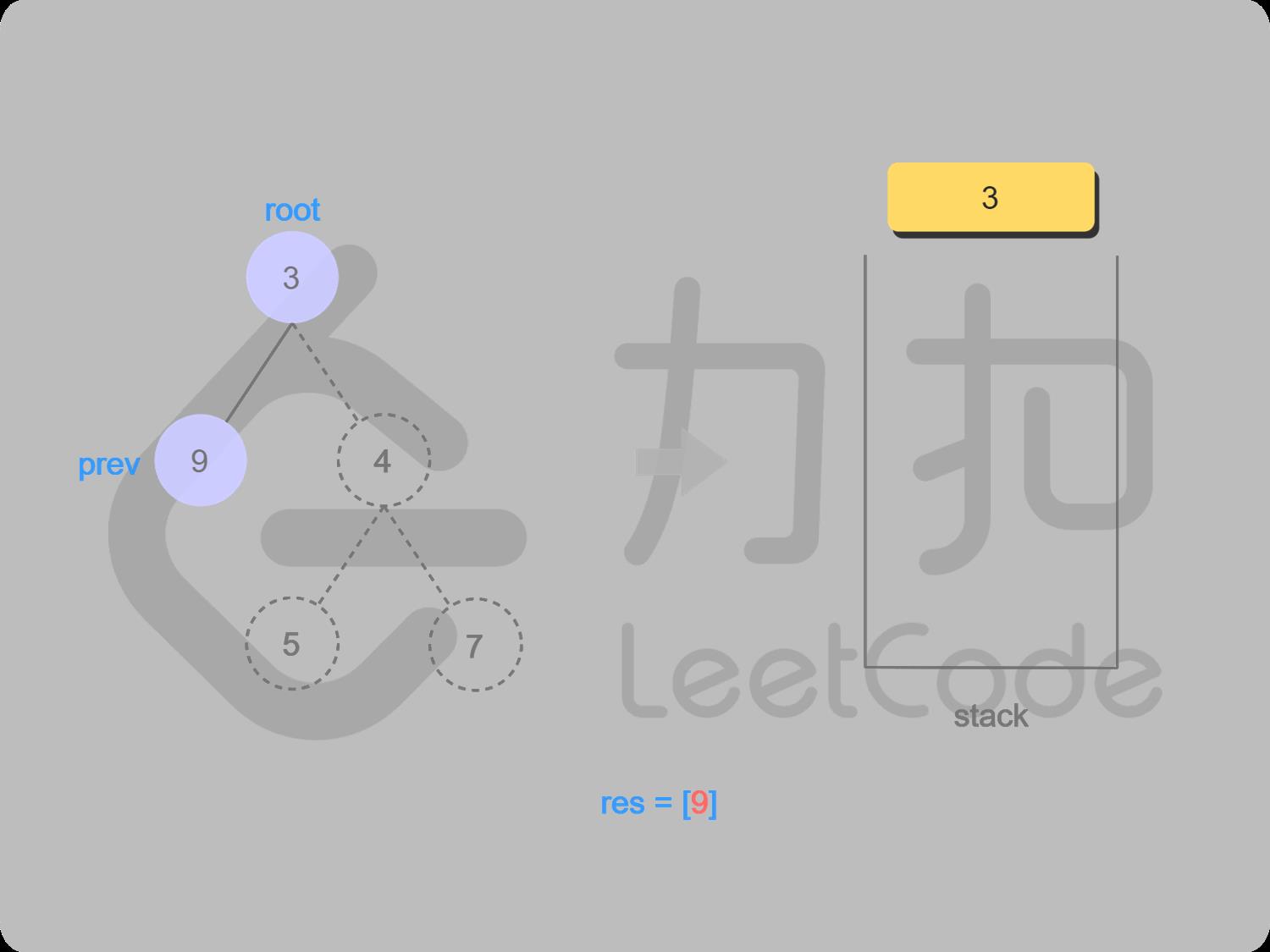
6 右结点4不为空,并且未访问,访问右结点4
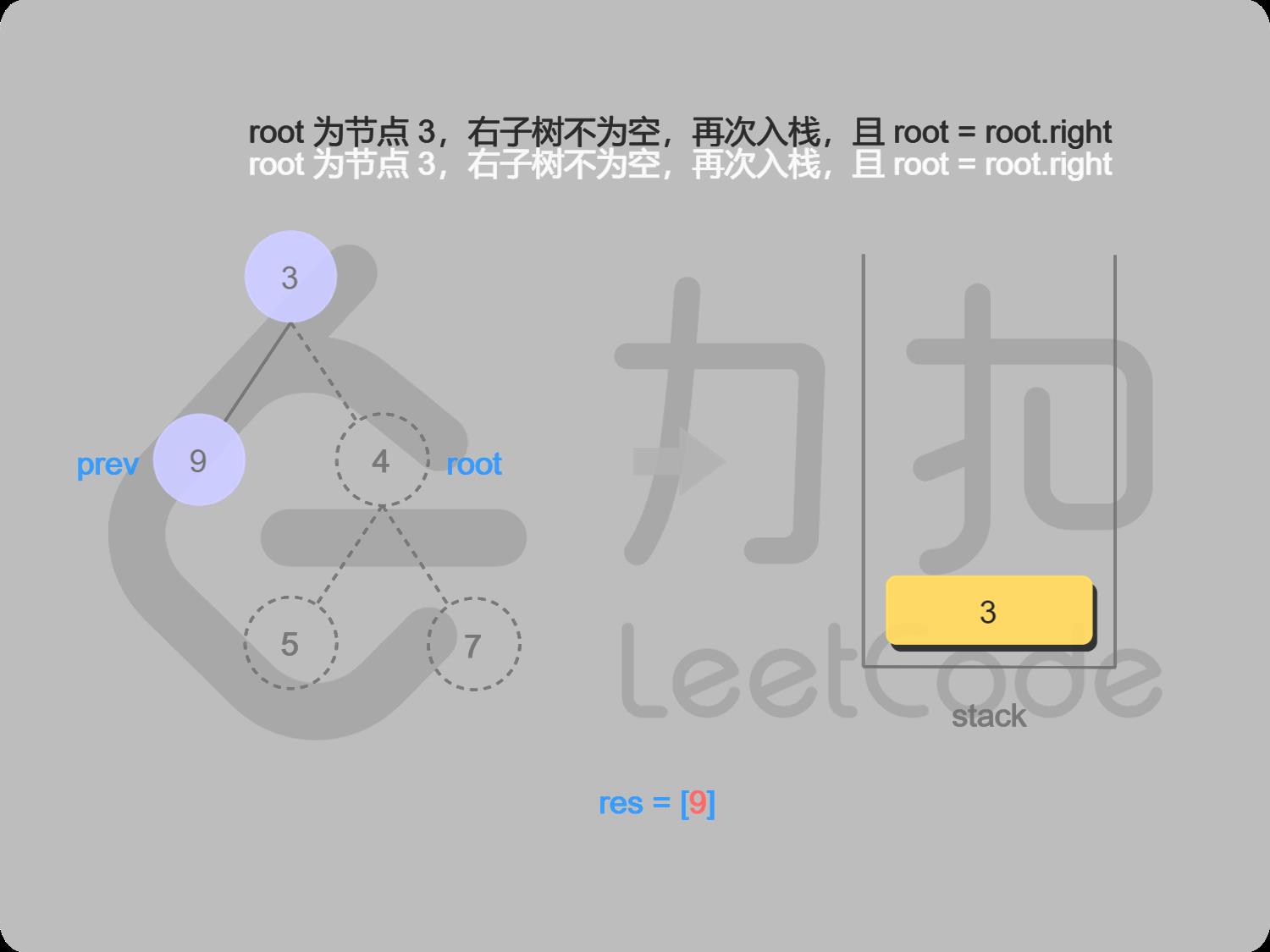
7 4入栈,找4的左子结点,左子结点5不为空
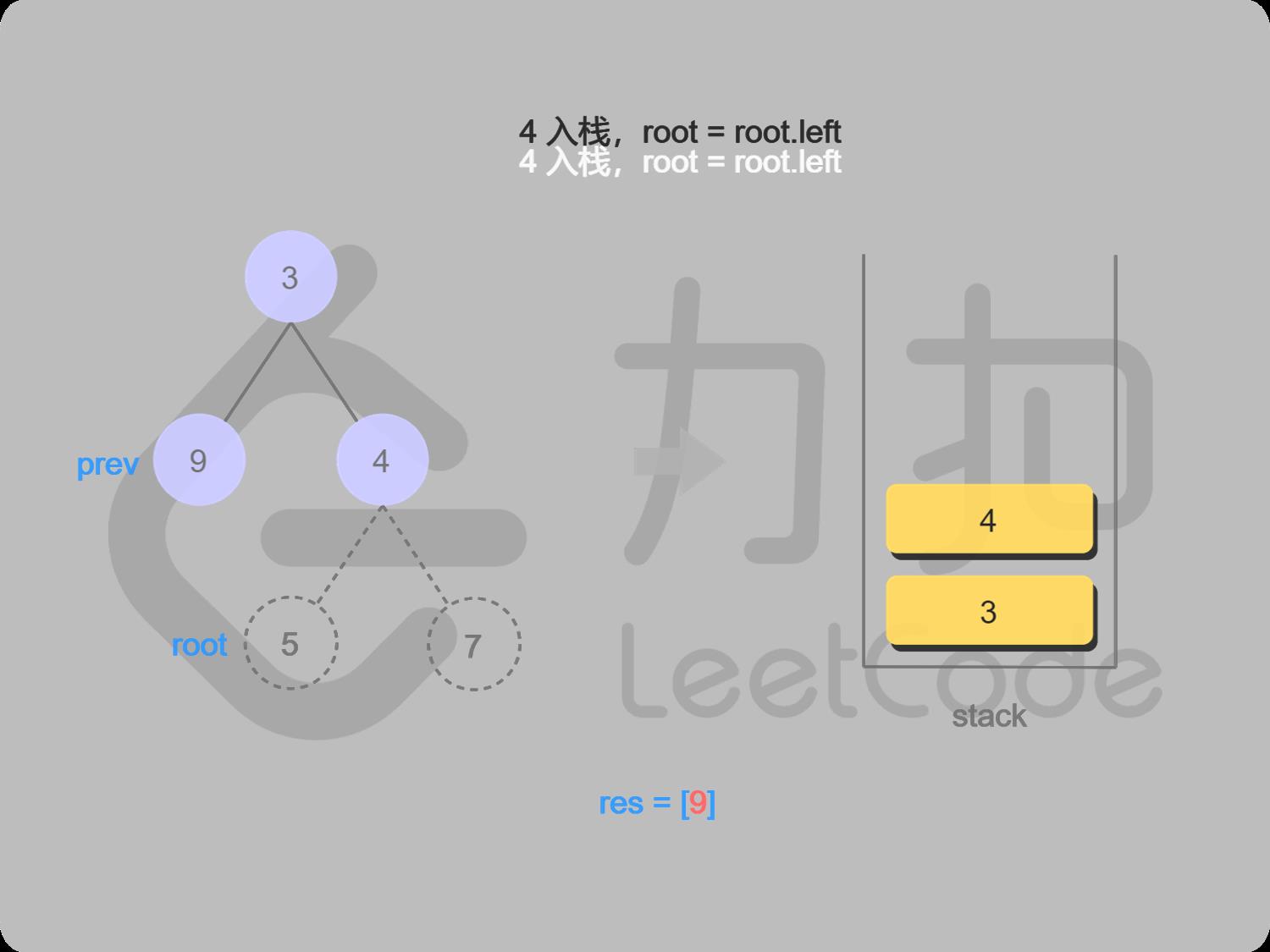
8 5入栈,找5的左子结点,左结点为空
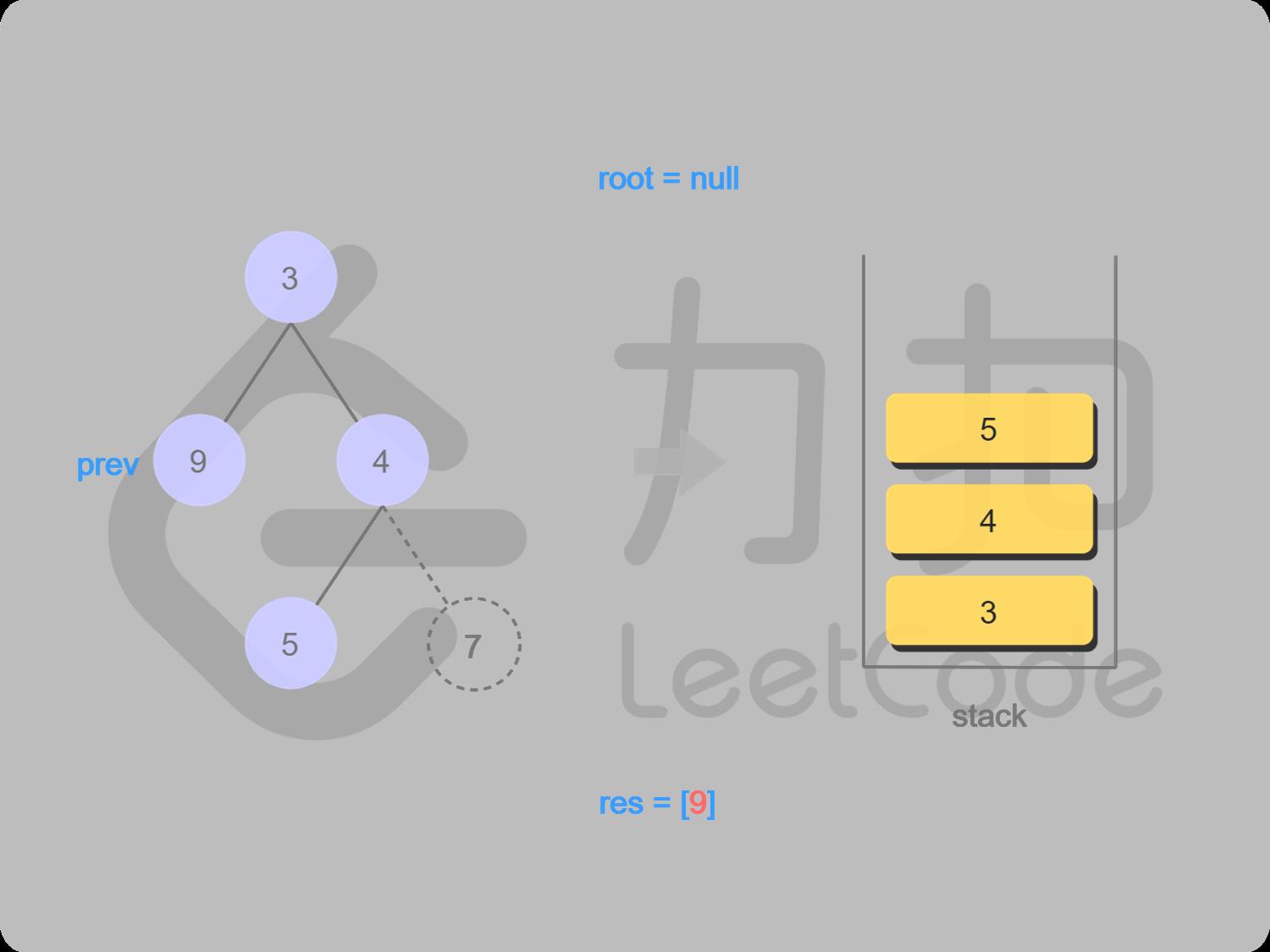
9 取栈顶值5(不出栈),5的右子结点为空,
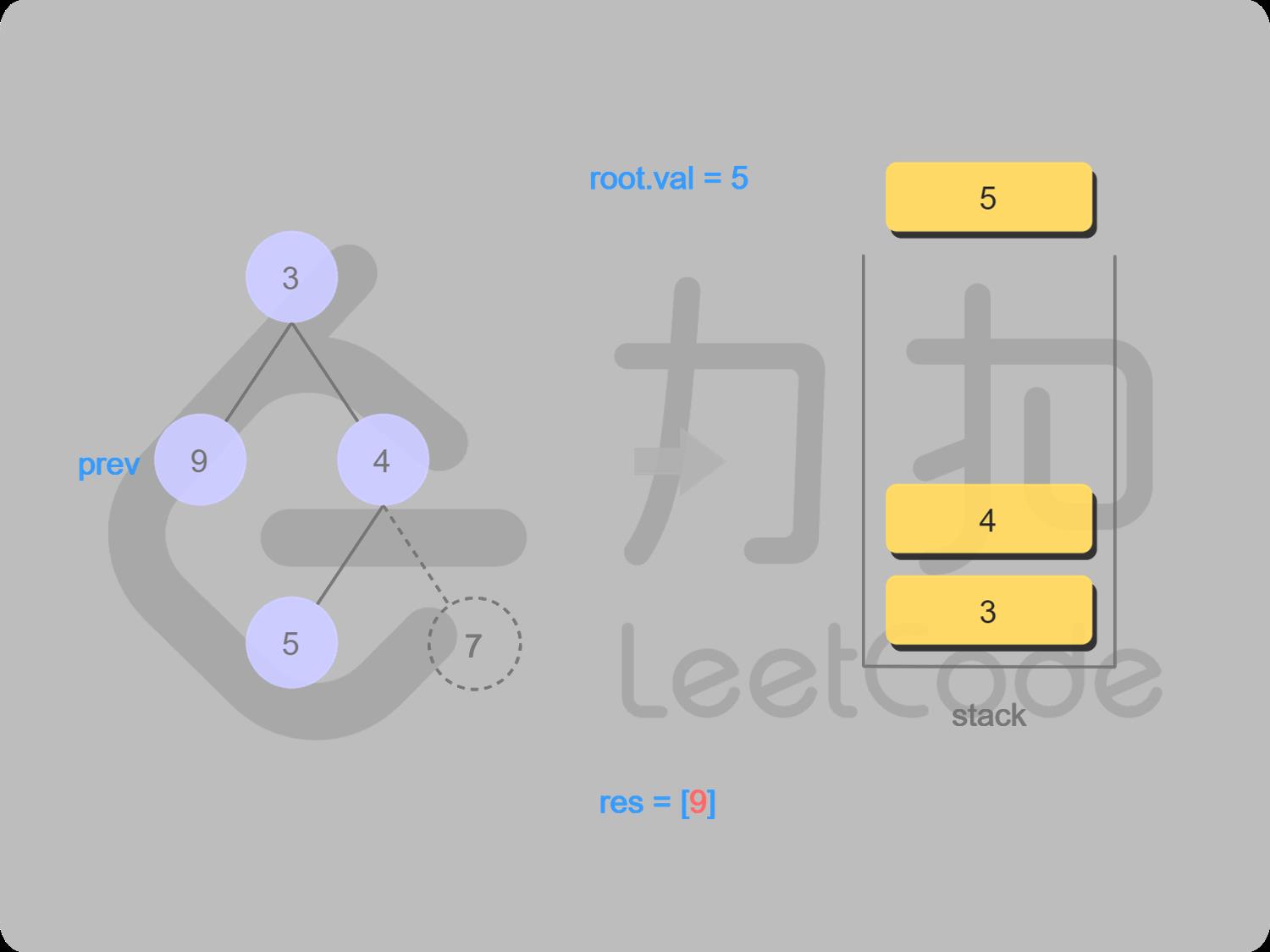
10 5的右结点为空,可以输出根结点,5出栈并输出,5变成上一个访问过的结点
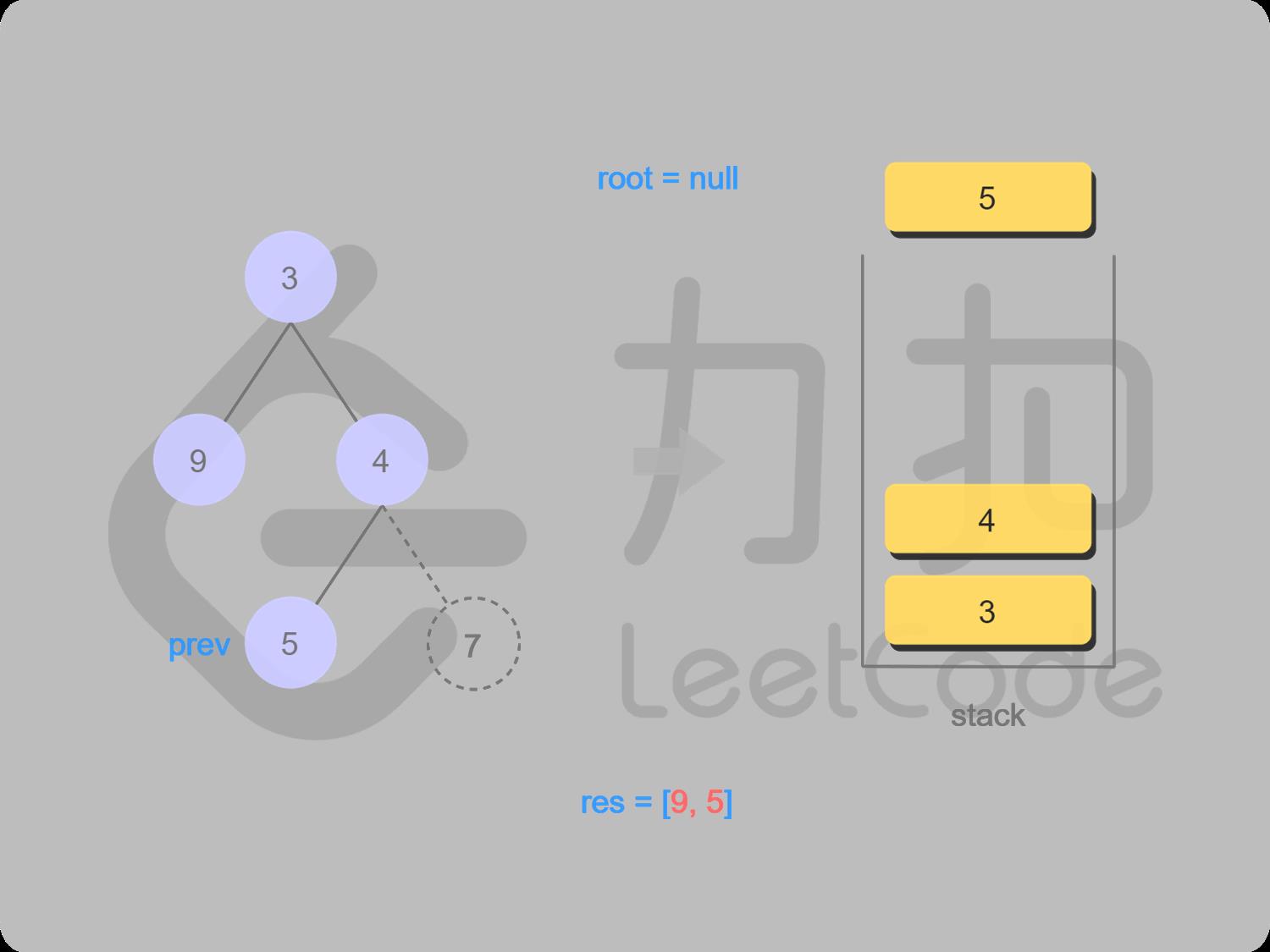
11 取栈顶值4(不出栈), 找4的右子结点7,右结点7存在并且未访问过,转到右结点7
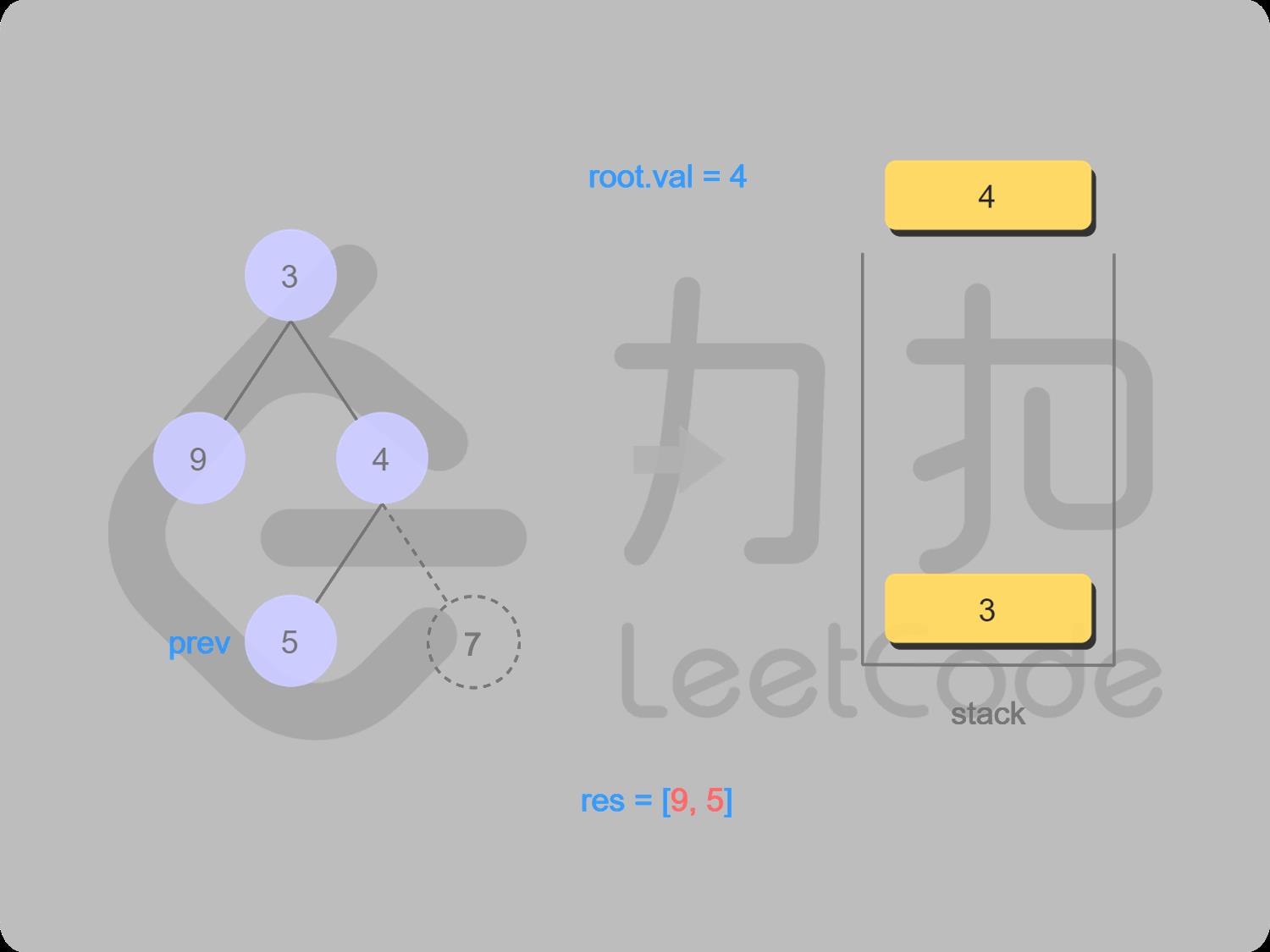
12 4的右结点7存在并且未访问过,转到右结点7
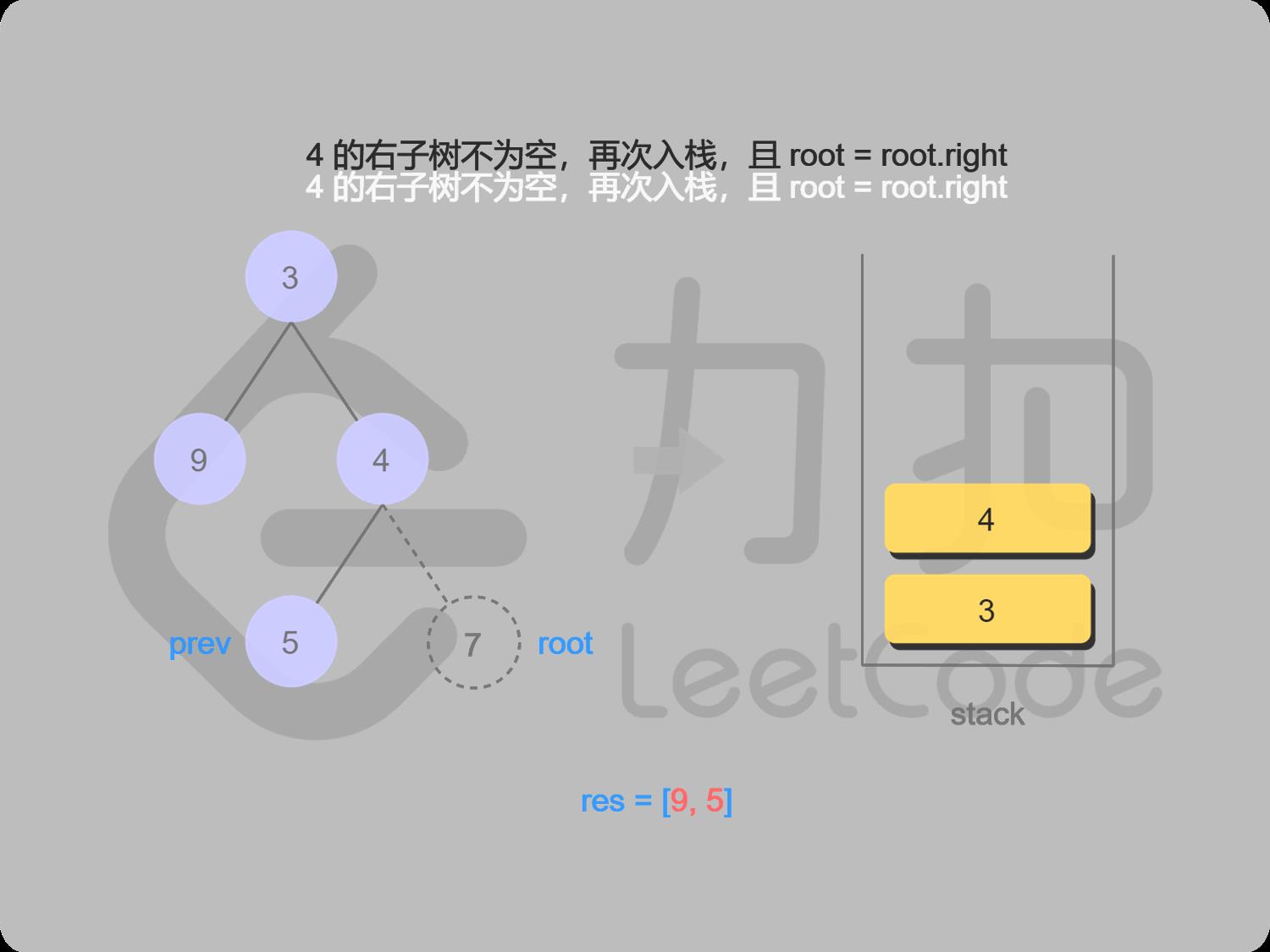
13 7入栈,找7的左子结点,左子结点为空
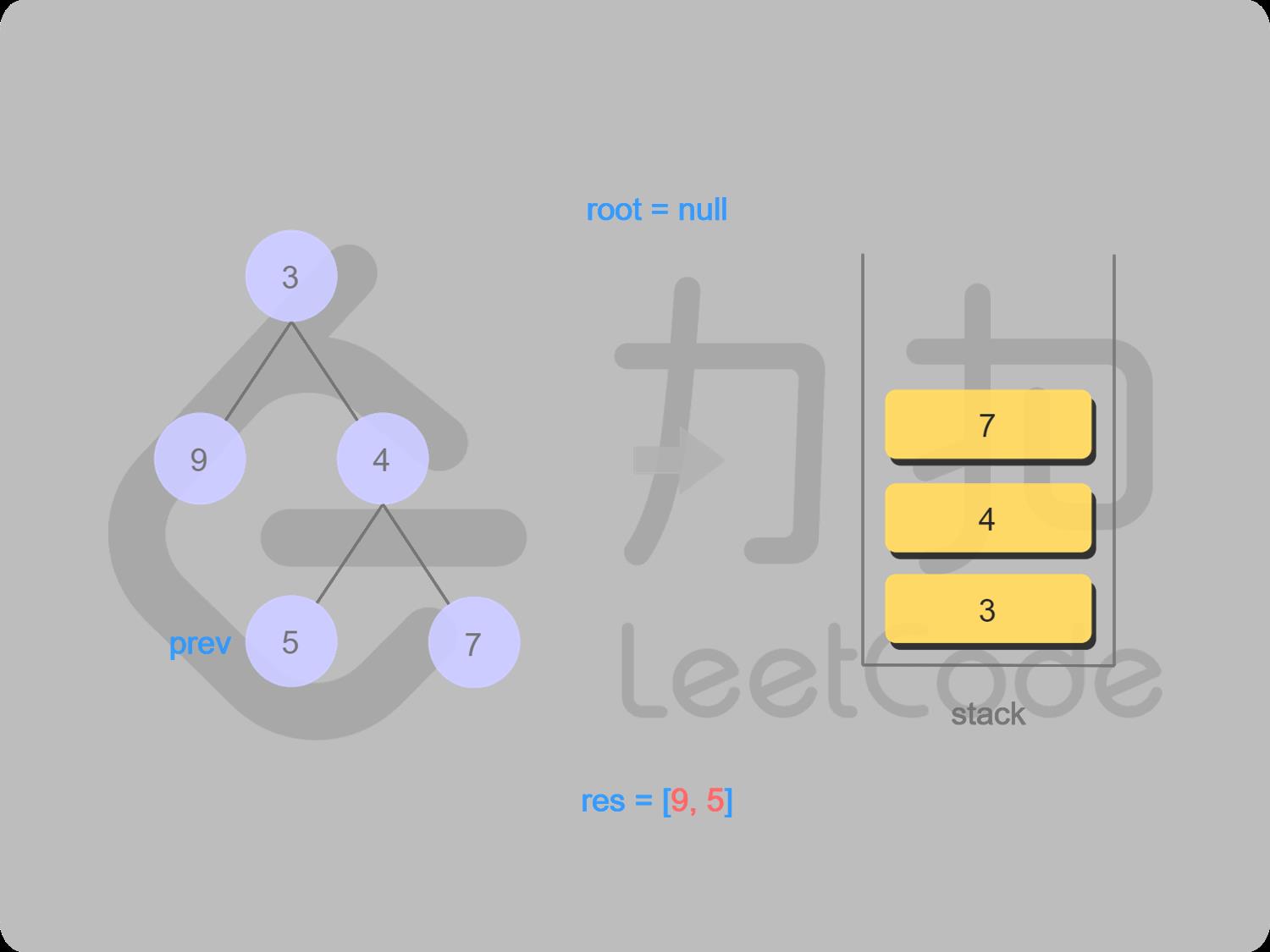
14 取栈顶值7(不出栈),找7的右子结点,右结点为空
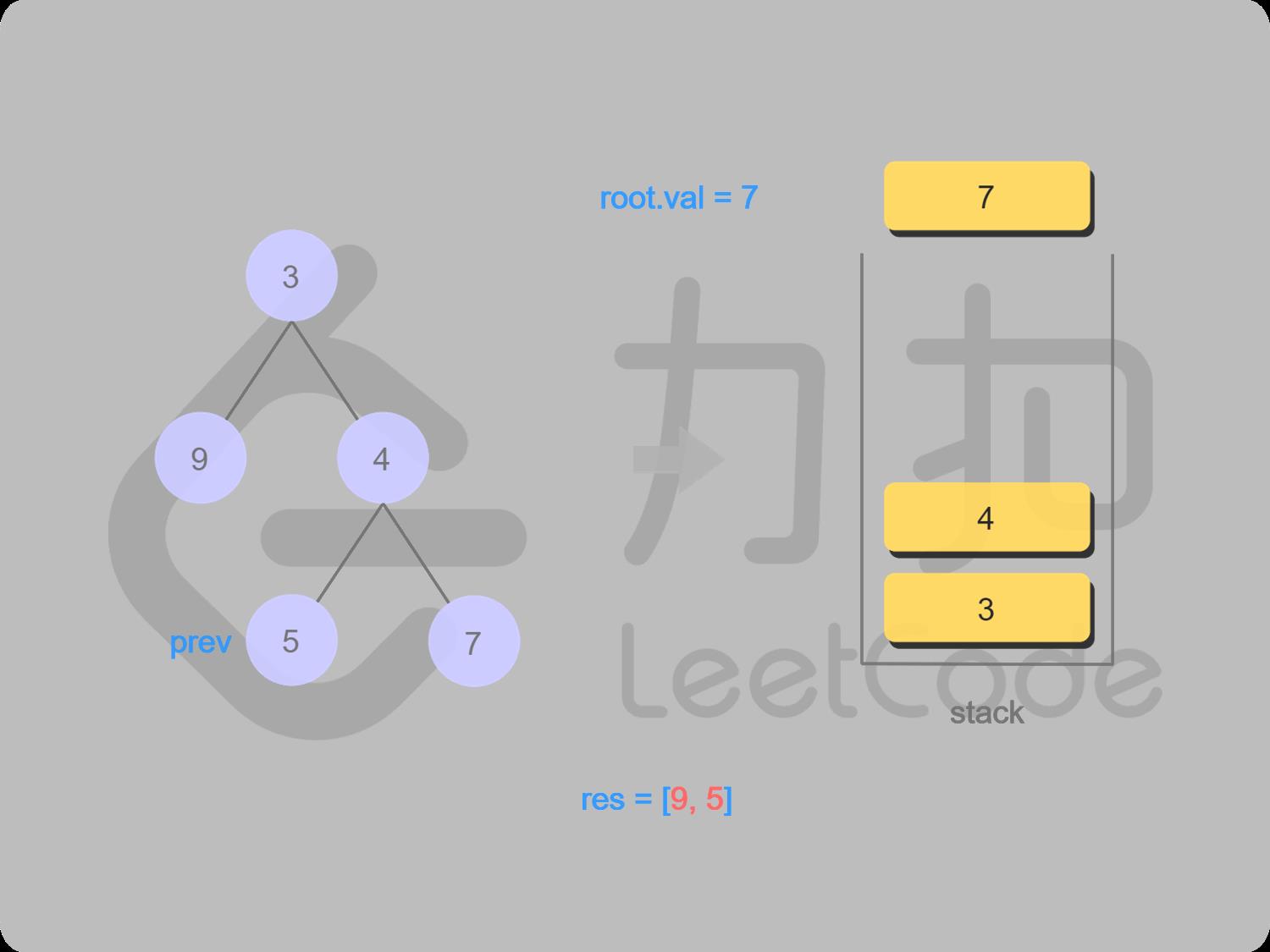
15 7右结点为空,7出栈并输出,7变成上一个被访问的结点
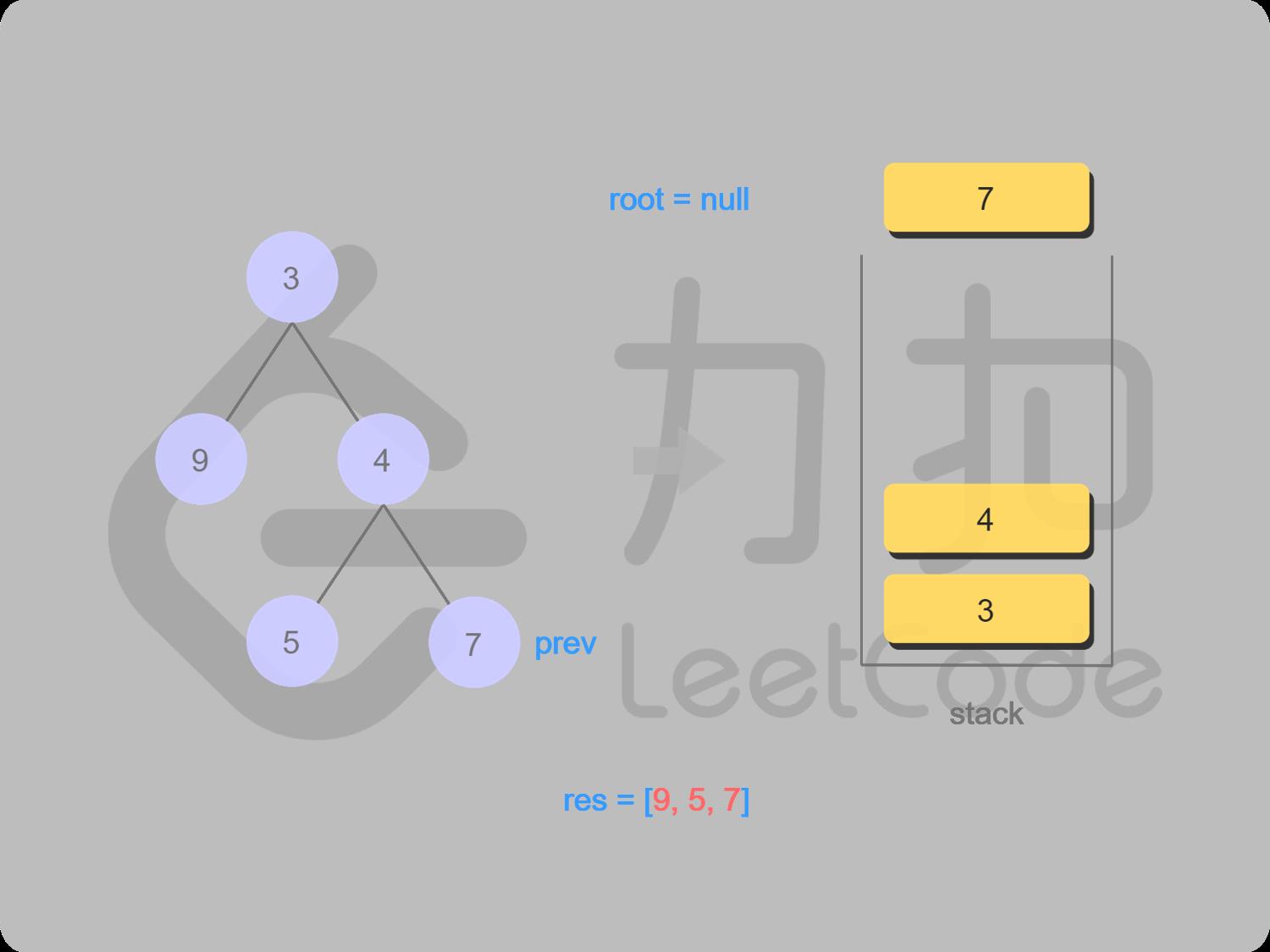
16 取栈顶值4(不出栈),右子结点7存在,并且是上一个被访问过的
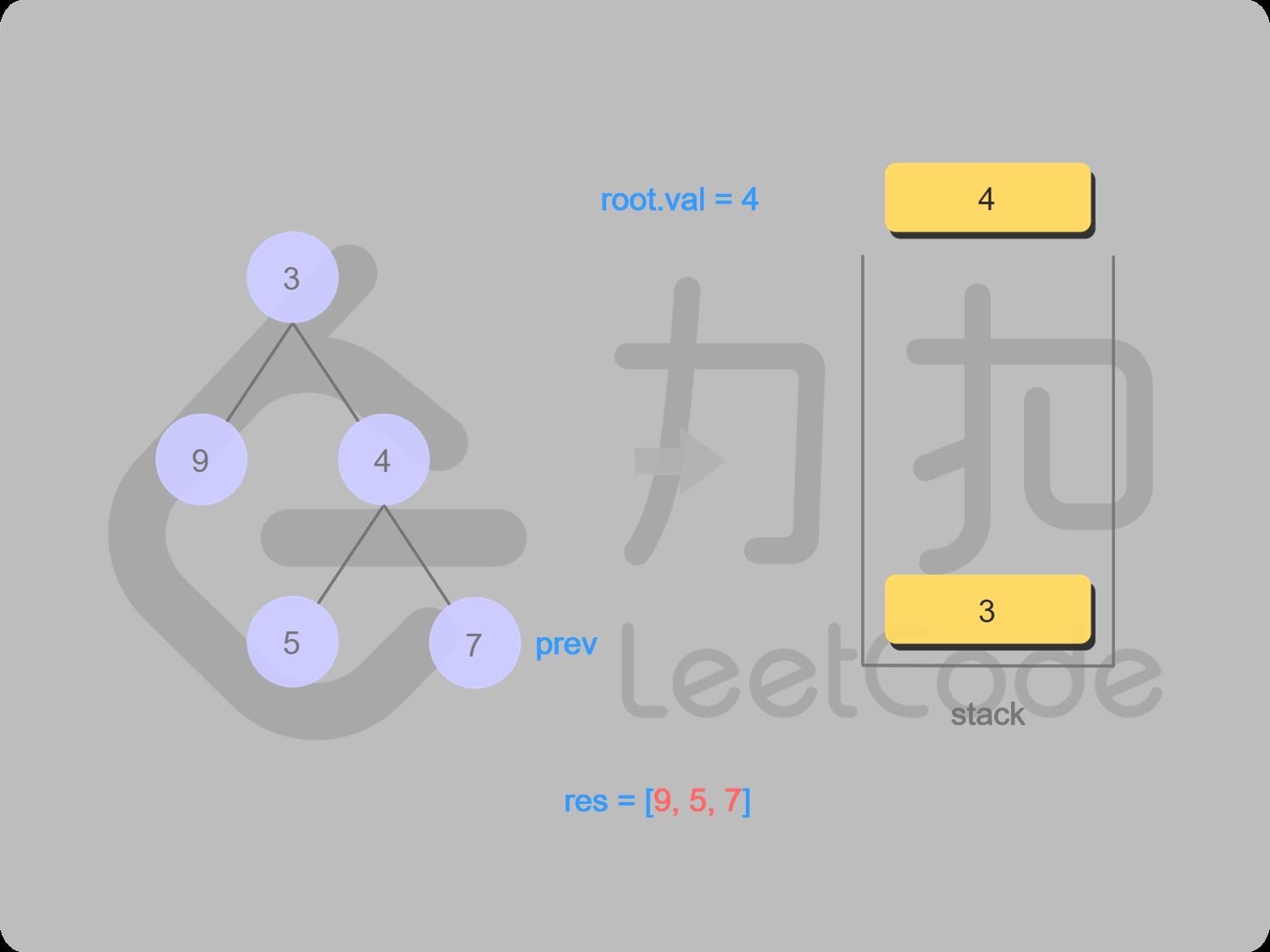
17 4的右子结点是上一个被访问的,4出栈并输出,4变成上一个被访问的结点
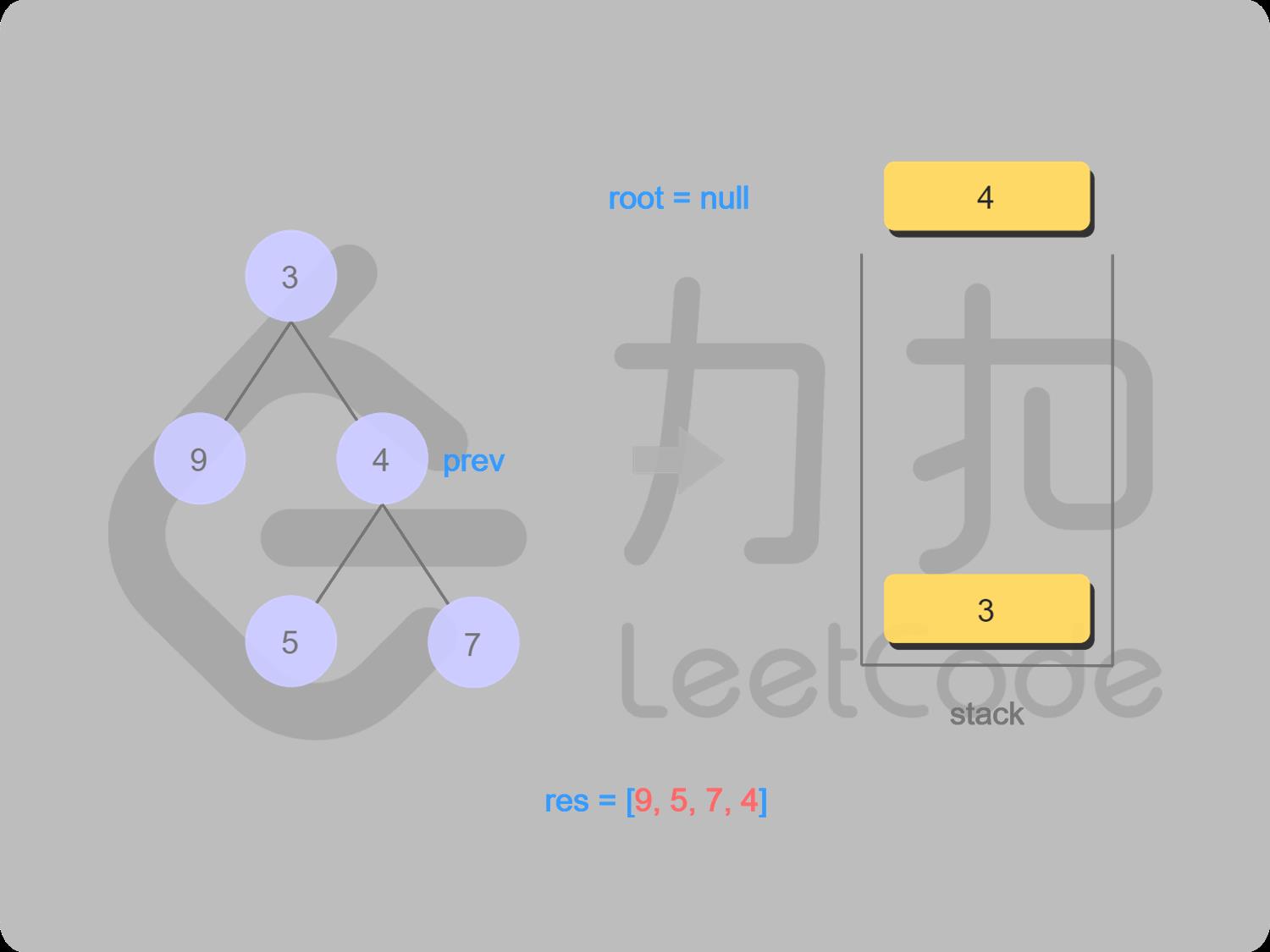
18 取栈顶值3(未出栈),3的右子结点是上一个被访问的结点,3出栈并输出
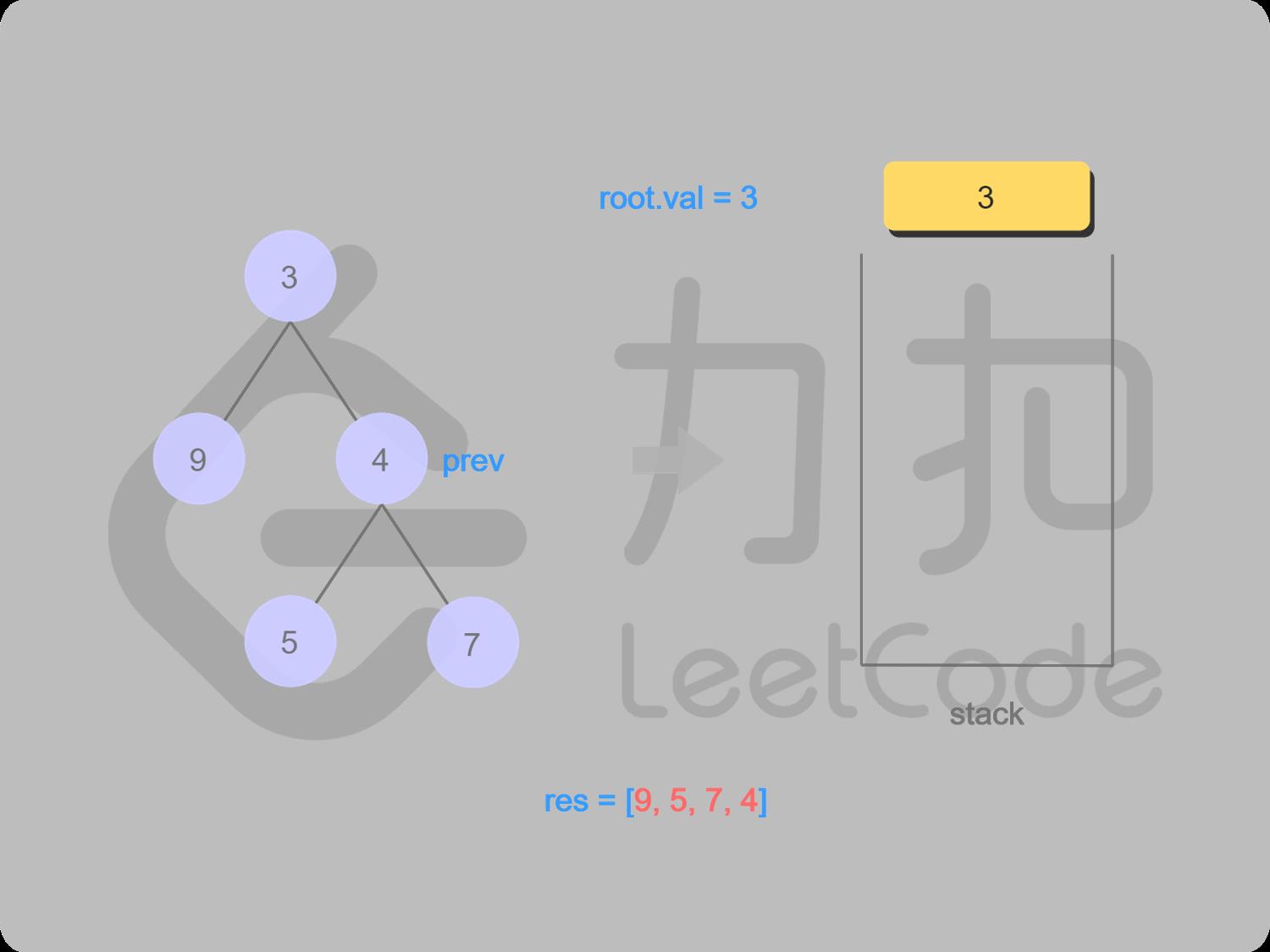
19 栈空,后序遍历完成
后序遍历代码:
//后序遍历(非递归)
void treePostPrint(Tree tree) //后序遍历与前两种不太一样,需要找一个变量存一下上一个访问的结点
cout << "后序遍历:"; //因为要把左右结点都循环完才能输出根结点,
stack<Tree> nodes;
Tree lastnode;
while (tree != NULL || !nodes.empty())
while (tree != NULL) //左结点不为空就一直找到底,把结点保存到栈里面
nodes.push(tree);
tree = tree->leftchild;
tree = nodes.top(); //此结点左子结点不存在,拿到这个根结点
if (tree->rightchild == NULL || lastnode == tree->rightchild) //看右结点是否存在或者是否被访问(如果右结点被访问了,可以输出根结点了)
cout << tree以上是关于22计算机408考研—数据结构—树定义,遍历,Huffman,并查集的主要内容,如果未能解决你的问题,请参考以下文章
22计算机408考研—数据结构—树定义,遍历,Huffman,并查集