路径规划基于蚁群算法求解TSP问题

Posted 2021-05-12 Matlab工程师

​问题定义：巡回旅行商问题

给定一组n个城市和俩俩之间的直达距离，寻找一条闭合的旅程，使得每个城市刚好经过一次且总的旅行距离最短。TSP问题也称为货郎担问题，是一个古老的问题。最早可以追溯到1759年Euler提出的骑士旅行的问题。1948年，由美国兰德公司推动，TSP成为近代组合优化领域的典型难题。TSP是一个具有广泛的应用背景和重要理论价值的组合优化问题。近年来，有很多解决该问题的较为有效的算法不断被推出，例如Hopfield神经网络方法，模拟退火方法以及遗传算法方法等。TSP搜索空间随着城市数n的增加而增大,所有的旅程路线组合数为(n-1)!/2。在如此庞大的搜索空间中寻求最优解，对于常规方法和现有的计算工具而言，存在着诸多计算困难。借助蚁群算法的搜索能力解决TSP问题，是很自然的想法。

根据仿生学家的研究结果,蚂蚁凭借路径寻优的能力能够找到蚁巢与食物之间的最短路径,其原理在于:蚂蚁在所经过的路径上留下一种挥发性分泌物(pheromone,以下称为信息素),信息素随着时间的推移会逐渐挥发消失.蚂蚁在觅食过程中能够感知这种物质的存在及其强度,并以此来指导自己的运动方向,倾向于朝着这种物质强度高的方向移动,即选择该路径的概率与当时这条路径上该物质的强度成正比.信息素强度越高的路径,选择它的蚂蚁就越多,则在该路径上留下的信息素的强度就更大,而强度大的信息素又吸引更多的蚂蚁,从而形成一种正反馈.通过这种正反馈,蚂蚁最终可以发现最佳路径,导致大部分的蚂蚁都会走此路径.

2.蚁群算法基本原理

2.1 算法综述

　　对于VRP问题,求解算法大致可分为精确算法和人工智能算法两大类。精确性算法基于严格的数学手段,在可以求解的情况下,解的质量较好。但是由于算法严格,运算量大,特别是大规模的问题几乎无法求解。所以其应用只能是小规模的确定性问题，面对中小规模问题,人工智能算法在精度上不占优势。但规模变大时,人工智能方法基本能在可接受时间里,找到可接受的满意解,这是精确算法难以做到的。由于的实际问题,各种约束错综复杂,人工智能算法显示出了巨大的优越性,也正因为如此,实际应用中,人工智能算法要更广泛。求解车辆路径调度问题的精确算法有动态规划法、分枝定界法等。并开始寻求所得结果可接受的启发式算法,以处理大规模实际问题，一些其他学科的新一代优化算法相继出现,如禁忌搜索算法,遗传算法,人工神经网络算法,以及现在研究较多的蚁群算法等。

2.2 蚁群算法的原理

　　蚁群算法是受到对真实蚂蚁群觅食行为研究的启发而提出。生物学研究表明：一群相互协作的蚂蚁能够找到食物和巢穴之间的最短路径,而单只蚂蚁则不能。生物学家经过大量细致观察研究发现,蚂蚁个体之间的行为是相互作用相互影响的。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称之为信息素的物质,而此物质恰恰是蚂蚁个体之间信息传递交流的载体。蚂蚁在运动时能够感知这种物质,并且习惯于追踪此物质爬行,当然爬行过程中还会释放信息素。一条路上的信息素踪迹越浓,其它蚂蚁将以越高的概率跟随爬行此路径,从而该路径上的信息素踪迹会被加强,因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象。某一路径上走过的蚂蚁越多,则后来者选择该路径的可能性就越大。蚂蚁个体之间就是通过这种间接的通信机制实现协同搜索最短路径的目标的。我们举例简单说明蚂蚁觅食行为：

​

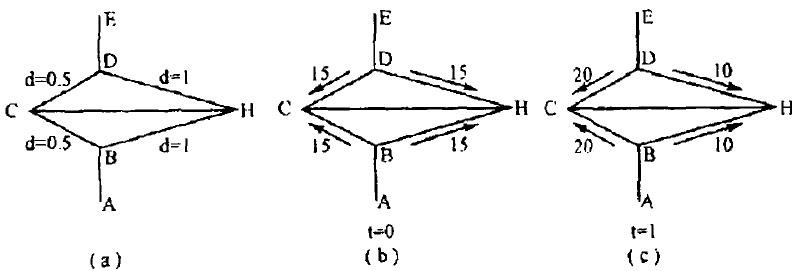
如上图a,b,c的示意图：

a图是原始状态，蚂蚁起始点为A，要到达E，中途有障碍物，要绕过才能到达。BC和BH是绕过障碍物的2条路径(假设只有2条)。各个路径的距离d已经标定。

b图是t=0时刻蚂蚁状态，各个边上有相等的信息素浓度，假设为15；

c图是t=1时刻蚂蚁经过后的状态，各个边的信息素浓度，有变化；因为大量蚂蚁的选择概率会不一样，而选择概率是和路径长度相关的。所以越短路径的浓度会越来越大，经过此短路径达到目的地的蚂蚁也会比其他路径多。这样大量的蚂蚁实践之后就找到了最短路径。所以这个过程本质可以概括为以下几点：

1.路径概率选择机制信息素踪迹越浓的路径,被选中的概率越大

2.信息素更新机制路径越短,路径上的信息素踪迹增长得越快

3.协同工作机制蚂蚁个体通过信息素进行信息交流。

从蚂蚁觅食的原理可见,单个个体的行为非常简单蚂蚁只知道跟踪信息素爬行并释放信息素,但组合后的群体智能又非常高蚂蚁群能在复杂的地理分布的清况下,轻松找到蚁穴与食物源之间的最短路径。这种特点恰恰与元启发算法的特点相一致,蚁群优化算法正是受到这种生态学现象的启发后加以模仿并改进而来,觅食的蚂蚁由人工蚁替代,蚂蚁释放的信息素变成了人工信息素,蚂蚁爬行和信息素的蒸发不再是连续不断的,而是在离散的时空中进行。

　　上述例子如果不好理解，我在这里贴几张PPT，个人感觉非常不错，也是我找了很多资料觉得最好理解的【来源是大连理工大学谷俊峰】，点击这里提供下载：蚁群算法基本知识.rar。

​

​

​

从深层意义上来讲,蚁群算法作为优化的方法之一,属于人工群集智能领域。人工群集智能,大都受自然群集智能如昆虫群和动物群等的启发而来。除了具有独特的强有力的合作搜索能力外,还可以利用一系列的计算代理对问题进行分布式处理,从而大大提高搜索效率。

回到目录

3.蚁群算法的基本流程

　　我们还是采用大连理工大学谷俊峰的PPT来说明问题，重要公式进行截图计算和解释，对PPT难以理解的地方进行单独解释：

3.1 基本数学模型

　　首先看看基本TSP问题的基本数学模型：

​

　　问题其实很简单，目标函数就是各个走过路径的总长度，注意的就是距离矩阵根据实际的问题不一样，长度是不一样的。

3.2 蚁群算法说明

　　在说明群蚁算法流程之前，我们对算法原理和几个注意点进行描述：

1.TSP问题的人工蚁群算法中，假设m只蚂蚁在图的相邻节点间移动，从而协作异步地得到问题的解。每只蚂蚁的一步转移概率由图中的每条边上的两类参数决定：1. 信息素值也称信息素痕迹。2.可见度，即先验值。 2.信息素的更新方式有2种，一是挥发，也就是所有路径上的信息素以一定的比率进行减少，模拟自然蚁群的信息素随时间挥发的过程；二是增强，给评价值“好”(有蚂蚁走过)的边增加信息素。 3.蚂蚁向下一个目标的运动是通过一个随机原则来实现的，也就是运用当前所在节点存储的信息，计算出下一步可达节点的概率，并按此概率实现一步移动，逐此往复，越来越接近最优解。 4.蚂蚁在寻找过程中，或者找到一个解后，会评估该解或解的一部分的优化程度，并把评价信息保存在相关连接的信息素中。

3.3 蚁群算法核心步骤

　　更加我们前面的原理和上述说明，群蚁算法的2个核心步骤是 路径构建 和 信息素更新。我们将重点对这2个步骤进行说明。

3.3.1 路径构建

　　每个蚂蚁都随机选择一个城市作为其出发城市，并维护一个路径记忆向量，用来存放该蚂蚁依次经过的城市。蚂蚁在构建路径的每一步中，按照一个随机比例规则选 择下一个要到达的城市。随机概率是按照下列公式来进行计算的：

​

　　上述公式就是计算 当前点 到 每一个可能的下一个节点 的概率。分子是 信息素强度 和 能见度 的幂乘积，而分母则是所有 分子的和值。这个刚开始是很不容易理解的，我们在最后实例计算的时候，可以看得很清楚，再反过来理解公式。注意每次选择好节点后，就要从可用节点中移除选择的节点。

3.3.2 信息素更新

　　信息素更新是群蚁算法的核心。也是整个算法的核心所在。算法在初始期间有一个固定的浓度值，在每一次迭代完成之后，所有出去的蚂蚁回来后，会对所走过的路线进行计算，然后更新相应的边的信息素浓度。很明显，这个数值肯定是和蚂蚁所走的长度有关系的，经过一次次的迭代， 近距离的线路的浓度会很高，从而得到近似最优解。那我们看看信息素更新的过程。

　　初始化信息素浓度C(0)，如果太小，算法容易早熟，蚂蚁会很快集中到一条局部最优路径上来，因为可以想想，太小C值，使得和每次挥发和增强的值都差不多，那么 随机情况下，一些小概率的事件发生就会增加非最优路径的信息素浓度；如果C太大，信息素对搜索方向的指导性作用减低，影响算法性能。一般情况下，我们可以使用贪婪算法获取一个路径值Cnn，然后根据蚂蚁个数来计算C(0) = m/Cnn ,m为蚂蚁个数

　　每一轮过后，问题空间中的所有路径上的信息素都会发生蒸发,然后，所有的蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素，公式如下：

​

​

　　信息素更新的作用： 1.信息素挥发(evaporation)信息素痕迹的挥发过程是每个连接上的 信息素痕迹的浓度自动逐渐减弱的过程，这个挥发过程主要用于避 免算法过快地向局部最优区域集中，有助于搜索区域的扩展。 2.信息素增强(reinforcement)增强过程是蚁群优化算法中可选的部 分，称为离线更新方式（还有在线更新方式）。这种方式可以实现 由单个蚂蚁无法实现的集中行动。基本蚁群算法的离线更新方式是 在蚁群中的m只蚂蚁全部完成n城市的访问后，统一对残留信息进行 更新处理。

3.3.3 迭代与停止

　　迭代停止的条件可以选择合适的迭代次数后停止，输出最优路径，也可以看是否满足指定最优条件，找到满足的解后停止。最重要的是，我刚开始理解这个算法的时候，以为每一只蚂蚁走一条边就是一次迭代，其实是错的。这里算法每一次迭代的意义是：每次迭代的m只蚂蚁都完成了自己的路径过程，回到原点后的整个过程。

回到目录

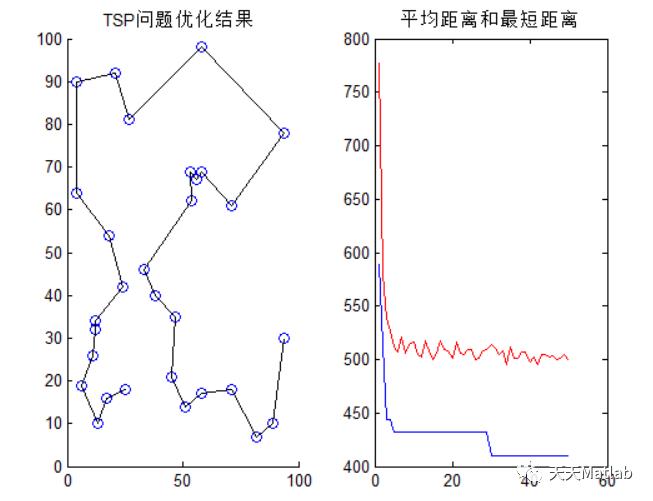
4.蚁群算法计算实例

　　使用PPT中的一个案例，非常直观，对几个符号错误进行了修改，主要是计算概率的乘号，结果没有错误：

​

​

​

​

​

​

　　过程总体还是比较简单的，注意理解公式，然后把公式和实例结合起来看，最好是拿笔自己手动画一画，容易理解。

​
% C表示n个城市的坐标，n×2的矩阵
% NC_max表示最大迭代次数
% m表示蚂蚁个数
% Alpha表示表征信息素重要程度的参数
% Beta表示表征启发式因子重要程度的参数
% Rho表示信息素蒸发系数
% Q表示信息素增加强度系数
% R_best表示各代最佳路线
% L_best表示各代最佳路线的长度
x=[51 27 56 21 4 6 58 71 54 53 94 18 89 33 12 25 24 58 71 94 17 38 13 82 12 58 45 11 47 4]\';
y=[14 81 67 92 64 19 98 18 62 69 30 54 10 46 34 18 42 69 61 78 16 40 10 7 32 17 21 26 35 90]\';
C=[x y];
NC_max=50;
m=30;
Alpha=1.4;
Beta=2.2;
Rho=0.15;
Q=10^6;
%%%%%%%%变量初始化%%%%%%%%%%%%%%%%
n=size(C,1); %n表示问题的规模（城市个数）
D=zeros(n,n);%D表示完全图的赋权邻接矩阵
for i=1:n
    for j=1:n
        if i~=j
           D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
           D(i,j)=eps;      
           %i=j时不计算，应该为0，但后面的启发因子要取倒数，用eps（浮点相对精度）表示
        end
        D(j,i)=D(i,j);   %对称矩阵
    end
end
Eta=1./D;                     %Eta为启发因子，这里设为距离的倒数
Tau=ones(n,n);                %Tau为信息素矩阵
Tabu=zeros(m,n);              %存储并记录路径的生成
NC=1;                         %迭代计数器，记录迭代次数
R_best=zeros(NC_max,n);       %各代最佳路线
L_best=inf.*ones(NC_max,1);   %各代最佳路线的长度
L_ave=zeros(NC_max,1);        %各代路线的平均长度
while NC<=NC_max              %停止条件之一：达到最大迭代次数，停止
%%%%%%%%将m只蚂蚁放到n个城市上%%%%%%%%%%%%
Randpos=[];                   %随即存取
for i=1:(ceil(m/n))
    Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))\';    
%%%%%%%%m只蚂蚁按概率函数选择下一座城市，完成各自的周游%%%%%%%%%%%%
for j=2:n                         %所在城市不计算
    for i=1:m     
        visited=Tabu(i,1:(j-1));  %记录已访问的城市，避免重复访问
        J=zeros(1,(n-j+1));       %待访问的城市
        P=J;                      %待访问城市的选择概率分布
        Jc=1;
    for k=1:n
        if length(find(visited==k))==0   %开始时置0
           J(Jc)=k;
           Jc=Jc+1;                       %访问的城市个数自加1
        end
    end
%下面计算待选城市的概率分布
    for k=1:length(J)
        P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);
    end
        P=P/(sum(P));
%按概率原则选取下一个城市
        Pcum=cumsum(P);          %cumsum，元素累加即求和
        Select=find(Pcum>=rand); %若计算的概率大于原来的就选择这条路线
        to_visit=J(Select(1));
        Tabu(i,j)=to_visit;
    end
end
if NC>=2
   Tabu(1,:)=R_best(NC-1,:);
end
%%%%%%%%记录本次迭代最佳路线%%%%%%%%%%%%
L=zeros(m,1);                        %开始距离为0，m*1的列向量
for i=1:m
    R=Tabu(i,:);
for j=1:(n-1)
    L(i)=L(i)+D(R(j),R(j+1));        %原距离加上第j个城市到第j+1个城市的距离
end
L(i)=L(i);              %一轮下来后走过的距离
end
L_best(NC)=min(L);                   %最佳距离取最小
pos=find(L==L_best(NC));
R_best(NC,:)=Tabu(pos(1),:);         %此轮迭代后的最佳路线
L_ave(NC)=mean(L);                   %此轮迭代后的平均距离
NC=NC+1;                             %迭代继续
%%%%%%%%更新信息素%%%%%%%%%%%%%%%%
Delta_Tau=zeros(n,n);                %开始时信息素为n*n的0矩阵
for i=1:m
    for j=1:(n-1)
        Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);           
%此次循环在路径（i，j）上的信息素增量
    end
Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
%此次循环在整个路径上的信息素增量
end
Tau=(1-Rho).*Tau+Delta_Tau;      %考虑信息素挥发，更新后的信息素
%%%%%%%%禁忌表清零%%%%%%%%%%%%
Tabu=zeros(m,n);                 %%直到最大迭代次数
end
%%%%%%%%结果%%%%%%%%%%%%
Pos=find(L_best==min(L_best));   %找到最佳路径（非0为真）
Shortest_Route=R_best(Pos(1),:)  %最大迭代次数后最佳路径
Shortest_Length=L_best(Pos(1))   %最大迭代次数后最短距离
figure(1)
subplot(1,2,1);                  %绘制第一个子图形
DrawRoute(C,Shortest_Route);     %画路线图的子函数
subplot(1,2,2);                  %绘制第二个子图形
plot(L_best);
hold on                        
plot(L_ave,\'r\');
title(\'平均距离和最短距离\')
​

​

​