路径规划基于粒子群优化蚁群的最短路径求解matlab源码

Posted 2021-06-16 MatlabQQ1575304183

蚁群算法，也是优化算法当中的一种。蚁群算法擅长解决组合优化问题。蚁群算法能够有效的解决著名的旅行商问题（TSP），不止如此，在其他的一些领域也取得了一定的成效，例如工序排序问题，图着色问题，网络路由问题等等。接下来便为大家简单介绍蚁群算法的基本思想。

蚁群算法，顾名思义就是根据蚁群觅食行为而得来的一种算法。单只蚂蚁的觅食行为貌似是杂乱无章的，但是据昆虫学家观察，蚁群在觅食时总能够找到离食物最近的路线，这其中的原因是什么呢？其实，蚂蚁的视力并不是很好，但是他们又是凭借什么区寻找到距离食物的最短路径的呢？经过研究发现，每一只蚂蚁在觅食的过程中，会在沿途释放出一种叫做信息素的物质。其他蚂蚁会察觉到这种物质，因此，这种物质会影响到其他蚂蚁的觅食行为。当一些路径上经过的蚂蚁越多时，这条路径上的信息素浓度也就越高，其他蚂蚁选择这条路径的可能性也就越大，从而更增加了这条路径上的信息素浓度。当然，一条路径上的信息素浓度也会随着时间的流逝而降低。这种选择过程被称之为蚂蚁的自催化行为，是一种正反馈机制，也可以将整个蚁群认定为一个增强型学习系统。

为了让大家更好的理解上文中提到的蚁群觅食行为，这里通过一张图片来说明蚁群觅食行为。

如图所示，A点为一个蚁穴，设定其中有两只蚂蚁，蚂蚁1和蚂蚁2。B点为食物所在位置，C点只是路径上的一点。假设ABC形成一个等边三角形，且两只蚂蚁的移动速度均相同。

在t0时刻，两只蚂蚁在蚁穴中，在他们面前有两条路可以选择，即AB或AC。两只蚂蚁随机进行选择，我们假设蚂蚁1选择了路径AC，而蚂蚁2选择了路径AB。

在t1时刻是，蚂蚁1走到了C点，而蚂蚁2走到了B点，即食物所在位置。他们在其经过的路径上释放了信息素，在途中用虚线表示。之后蚂蚁2将食物运往蚁穴，并依然在沿途释放信息素，蚂蚁1则从C点向B点进发。

等到t2时刻时，蚂蚁2到达了蚁穴A点，蚂蚁1到达了食物所在位置B点，此时蚂蚁2再次出发去搬运食物，它发现AB路径上的信息素浓度要高于AC路径上的信息素浓度（AB路径上有两条虚线，AC路径上只有1条虚线）。因此蚂蚁2选择AB路径去搬运食物，而蚂蚁1则在B点获取到了食物，接下来返回蚁穴，但是它也有两种选择，一种是原路返回，另一种便是走线路AB。蚂蚁1发现AB路径上的信息素浓度要高于AC路径上的信息素浓度，因此它将选择AB来返回蚁穴。

如此往复，AC路径的信息素浓度会越来越低，AB路径上的信息素浓度会越来越高，所以AC路径上将没有蚂蚁再次经过，两只蚂蚁都只会选择路径较短的AB线路去搬运食物。

 

clc
clear
close all
E=0.000001;
maxnum=30;%最大迭代次数
narvs=3;%目标函数的自变量个数
particlesize=20;%粒子群规模
c1=1.2;%每个粒子的个体学习因子，加速度常数
c2=1.6;%每个粒子的社会学习因子，加速度常数
w=0.8;%惯性因子
vmax1=0.5;%粒子的最大飞翔速度
vamx2=-0.5;
v=rand(particlesize,narvs);%粒子飞翔速度
x=zeros(particlesize,3);
x(:,1)=1+rand(1);
x(:,2)=7+rand(1);%粒子所在位置
x(:,3)=0.2+0.1*rand(1);
%定义适应度函数
% ROUT=zeros(particlesize,100);
for i=1:particlesize
    [TT(i),ROUT{i},f(i)]=ACO(x(i,1),x(i,2),x(i,3));
end
personalbest_x=x;
personalbest_faval=f;
% personalbest_faval=TT;
[globalbest_faval(1),i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);
globalbest_route=ROUT{i};
ff(1)=globalbest_faval(1);
k=2;
w

route=globalbest_route;
[minkl,p]=min(globalbest_faval);
xbest=globalbest_x(p,:);
LENROUT=length(route);
disp(['Alpha 表征信息素重要程度的参数=',num2str(xbest(1))]);
disp(['Beta 表征启发式因子重要程度的参数=',num2str(xbest(2))]);
disp(['Rho 信息素蒸发系数=',num2str(xbest(3))]);
disp(sprintf('Shortroad is: %s',num2str(route)));
disp(sprintf('Mininum is: %d',minkl));

figure(2)
% set(gcf,'color','white');
plot(1:length(ff),ff)
title('粒子群蚁群算法收敛曲线变化趋势')
xlabel('迭代次数');
ylabel('适应度值');

first_address = [
    100,10
    150,10
    170,30
    180,20
    200,10
    200,100
    200,150
    190,180
    180,200
    160,200
    170,180
    140,180
    135,200
    130,180
    100,200
    125,100
    200,300
    10,300
    10,200
    10,180
    10,100
    10,10
    50,30
    100,10
    ];%first_address表示测试数据中的节点坐标
SumOfCity = size(first_address,1);%节点个数，实际返回行数，即为节点个数


for   n=1:size(first_address)
    for m=1:size(first_address)
        if length_address(n,m)~=0
            length_address(m,n)=length_address(n,m);   %对称矩阵
        end
    end
end
MM=size(length_address,1);
% 画出节点分布图形
figure;
grid on;
hold on;
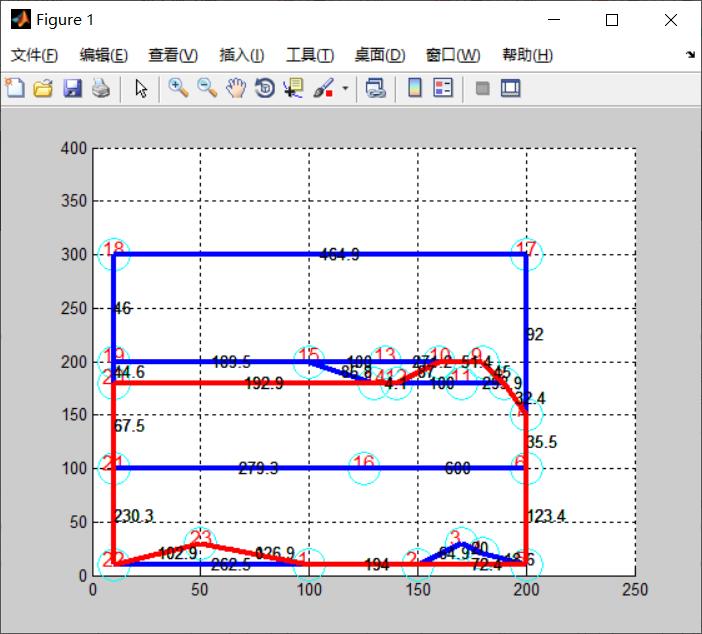
title (strcat('井下机车最短运输路径',date))
%title( sprintf('井下机车最短运输路径 Event occured at %s',datestr (date ,15)));
for i=1:MM-1
    plot(first_address(i,1),first_address(i,2),'bo','MarkerSize',10);
    str=num2str(i);
    text(first_address(i,1)-5,first_address(i,2)+5,str,'Color','red','FontSize',12);
end
% m=length(route);
for i=1:LENROUT
    plot(first_address(route(i),1),first_address(route(i),2),'MarkerSize',10,'MarkerEdgeColor','k','MarkerFaceColor',[0.5,0.5,0.5])  ;
    hold on;
end
for i=1:MM
    for j=1:MM
        if(length_address(i,j)~=0)
            line([first_address(i,1),first_address(j,1)],[first_address(i,2),first_address(j,2)],'Color','g','LineWidth',3);%划线
            text((first_address(i,1)+first_address(j,1))/2,(first_address(i,2)+first_address(j,2))/2,num2str(length_address(i,j)));%标注线段距离
        end
    end
end
%% 最短路径
for p=1:LENROUT-1
    if(route(p+1)~=24)
        line([first_address(route(p),1),first_address(route(p+1),1)],[first_address(route(p),2),first_address(route(p+1),2)],'Color','r','LineWidth',3);%划线
        text((first_address(route(p),1)+first_address(route(p+1),1))/2,(first_address(route(p),2)+first_address(route(p+1),2))/2,num2str(length_address(route(p),route(p+1))));%标注线段距离
    else
        line([first_address(route(p),1),first_address(1,1)],[first_address(route(p),2),first_address(1,2)],'Color','r','LineWidth',3);%划线
        text((first_address(route(p),1)+first_address(1,1))/2,(first_address(route(p),2)+first_address(1,2))/2,num2str(length_address(route(p),route(p+1))));%标注线段距离
    end
end
axis([0 250 0 400])
% 图形显示最优及平均函数值变化趋势
%  figure(2);
%  plot( minPL);
%  title('迭代优化过程');
%  xlabel('迭代次数');
%  ylabel('Cost');
%  hold on;

​

完整代码或者代写添加QQ1575304183