单目标优化求解基于matlab集成随机惯性权重和差分变异操作的樽海鞘群算法（ISSA）求解单目标问题含Matlab源码 1858期

Posted 2022-05-25 海神之光

一、集成随机惯性权重和差分变异操作的樽海鞘群算法简介

为了提高樽海鞘群算法（Salp Swarm Algorithm,SSA）的收敛速度、计算精度和全局优化能力,在分析总结粒子群优化（Particle Swarm Optimization,PSO）和差分进化（Differential Evolution,DE）算法相关研究成果后,提出了一种集成PSO算法随机惯性权重和DE算法差分变异操作的改进SSA算法——iSSA。首先,将PSO算法的随机惯性权重引入SSA算法的追随者位置更新公式中,用于增强和平衡SSA算法的勘探与开发能力;其次,用DE算法的变异操作替代SSA算法的领导者位置更新操作,以提高SSA算法的收敛速度和计算精度。为了检验随机惯性权重和差分变异操作对SSA算法的改进效果,在多个高维基准函数上进行了仿真实验,并与其他改进SSA算法进行了比较。实验结果及分析表明,与SSA算法和两个典型的改进SSA算法（ESSA和CASSA）相比,集成随机惯性权重和差分变异操作的iSSA算法,在没有增加算法时间复杂度的情况下,显著地提高了SSA算法的收敛速度、计算精度和全局优化能力,并且优于ESSA算法和CASSA算法。

1 本文改进SSA算法的基本策略
SSA算法的核心是领导者和追随者的位置更新操作。PSO算法和DE算法是目前群体智能算法的优秀代表,其丰富的研究成果为SSA算法的改进研究提供了大量有益的参考和启发。本文将PSO算法的随机惯性权重和DE算法的变异操作分别引入SSA算法的式(3)和式(1)中,用于弥补SSA算法的缺点。

1.1 PSO算法随机惯性权重的引入
由SSA算法中的式(3)可知,追随者i的第j维位置xij的更新操作直接受前一个追随者i-1的第j维位置xi−1j的影响。然而,在大多数情况下,追随者i-1的位置对应的解通常较差,从而导致SSA算法易陷入局部最优,收敛速度慢且计算精度低。

在PSO算法中,粒子速度更新直接决定着粒子位置更新。惯性权重是PSO算法粒子速度更新公式中的重要参数,它体现了上一代粒子对当前粒子速度更新的影响力,用于平衡PSO算法的勘探与开发。尽管迄今为止已有大量学者提出了各种PSO算法惯性权重控制策略,但研究表明,在总计18种PSO算法惯性权重控制策略中,除了随机惯性权重以外,常数项惯性权重优于其他所有的惯性权重控制策略。

常数项惯性权重需要繁琐的算法参数调校,因此本文将PSO算法的随机惯性权重引入SSA算法追随者位置更新操作中,从而得到追随者位置更新公式:
xij=12(xij+w×xi−1j)         (4)
其中,w为随机惯性权重系数,其取值方法如式(5)[16]所示:
w=0.5+Random (0,1)/2 (5)

其中,Random (0,1)表示均匀分布于(0,1)内的随机数,故w的取值范围为(0.5,1)。显然,此处引入的随机惯性权重没有改变SSA算法的时间复杂度。

1.2 集成DE算法的变异操作
根据SSA算法的式(1),在领导者位置更新操作中,参与者是食物源且没有追随者,缺乏樽海鞘之间的协作和信息共享,容易导致SSA算法过早收敛于较差的局部最优解。
变异操作是DE算法的重要组成部分,它一般通过3个不同的个体来为种群内每一个个体生成一个新个体,通过比例因子可以调节算法开发和勘探之间的平衡。目前DE算法研究中最典型的变异操作有5种,其中与SSA算法的式(1)一样包含最优解且形式最简单的变异操作一般简称为“DE/best/1”。
综上所述,本文提出用DE算法的上述变异操作来替代SSA算法领导者的位置更新操作,从而得到如式(6)所示的领导者位置更新操作:
xij=Fk+r×(xmj-xnj) (6)
针对式(1)和式(6),需要说明以下5点:
(1)根据SSA算法官方网站[18]提供的Matlab版源程序可知,式(1)中的x1j等同于式(6)中的xij,式(1)中的食物源Fj实际上是领导者x1j;只要樽海鞘i的适应度高于领导者的适应度,领导者就被樽海鞘i替代,食物源或最优解也随之被领导者或樽海鞘i替代。
(2)在式(6)中,随机数m和n是互异的樽海鞘编号,说明新生成的樽海鞘i是由最优解、樽海鞘m和樽海鞘n经过差分变异操作合成的。
(3)在式(6)中,互异的下标k和j意味着最优解的异维(跨维)分量参与差分变异操作,有益于增强搜索的广度(开发)和新个体的多样性,避免算法过早陷入局部最优。本文算法程序调试证实了此类异维差分变异操作带来的好处。
(4)式(6)中,系数r的作用类似于DE算法变异操作中的比例因子,经反复测试发现,其是取值范围在(0,1/3)的随机数时效果较好。
(5)与式(1)相比,本文提出的式(6)依然是一种一阶线性关系,没有增加SSA算法的时间复杂度。

二、部分源代码

clearvars
close all
clc


## 三、运行结果
![在这里插入图片描述](https://img-blog.csdnimg.cn/48997ee6641a48ee82890fe30fd0d5e8.jpeg#pic_center)

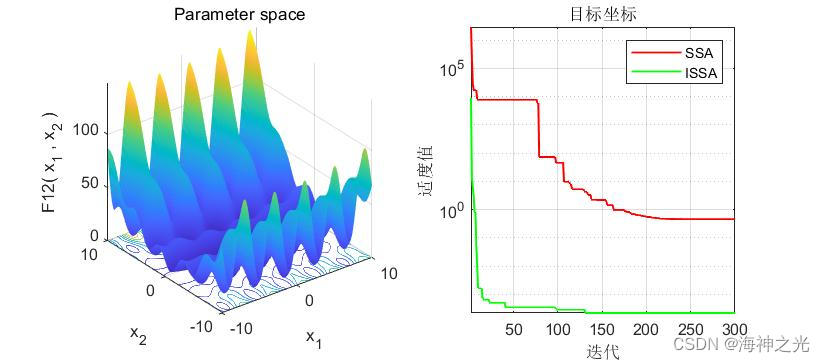
## 四、matlab版本及参考文献
**1 matlab版本**
2014a

**2 参考文献**
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]张志强,鲁晓锋,隋连升,李军怀.集成随机惯性权重和差分变异操作的樽海鞘群算法[J].计算机科学. 2020,47(08)

**3 备注**
简介此部分摘自互联网，仅供参考，若侵权，联系删除