单目标优化求解基于matlab粒子群混沌混合蝴蝶优化算法求解最优目标问题（HPSOBOA）含Matlab源码 1538期

Posted 2021-12-22 紫极神光

一、遗传算法简介

1 算法的种群初始化
设D维搜索空间中，随机生成初始解的表达式为：

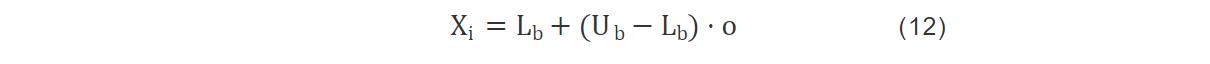
式中，Xi表示蝴蝶群体中第i只蝴蝶(i = 1, 2, 3, …, N)空间位置，N表示初始解的个数；Lb, Ub分别表示搜索空间的上界和下界；o表示(0, 1)之间的随机数矩阵。

2 算法的全局搜索
混合算法HPSBA的全局搜索阶段可表示为：

3 算法的局部搜索
混合算法HPSBA的局部搜索阶段可表示为：

式中，C1 = C2 = 2，r1、r2的取值为(0, 1)中的随机数。
4 控制参数c和ω
混沌理论在群智能优化算法中有着较多的应用研究，如：混沌种群初始化、控制参数混沌调节策略等。Logistic映射[15]的表达式为：

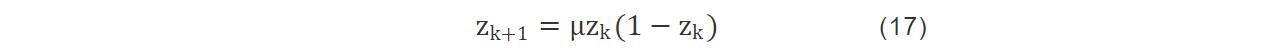
式中，k表示混沌映射的迭代次数；Logistic映射的混沌序列为(0, 1)，当μ=4时，该映射会产生混沌现象。

李雅普诺夫(Lyapunov)指数[16]作为判别混沌特性的一个重要指标。若混沌映射的最大Lyapunov指数越大，其混沌特性越明显、混沌程度越高。其表达式为：

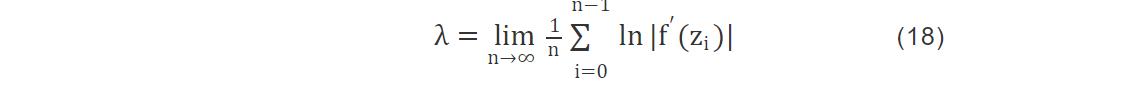
式中，λ表示李雅普诺夫指数；f′(z)表示混沌映射函数的一阶导数；n表示混沌映射的迭代次数。

取参数μ∈(3,4]绘制分岔图和Lyapunov指数曲线，如图2所示。


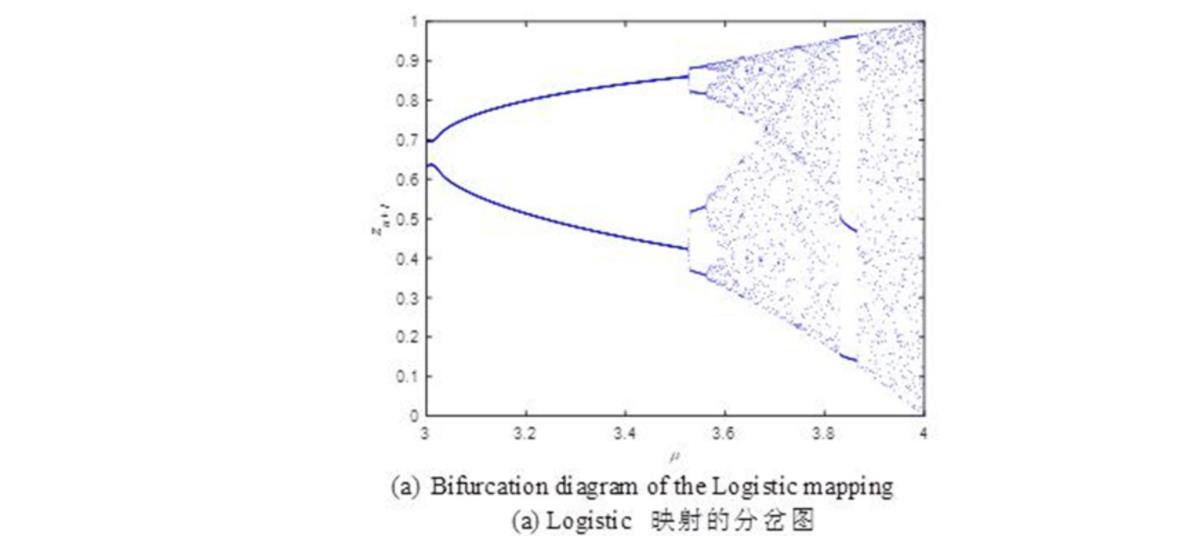
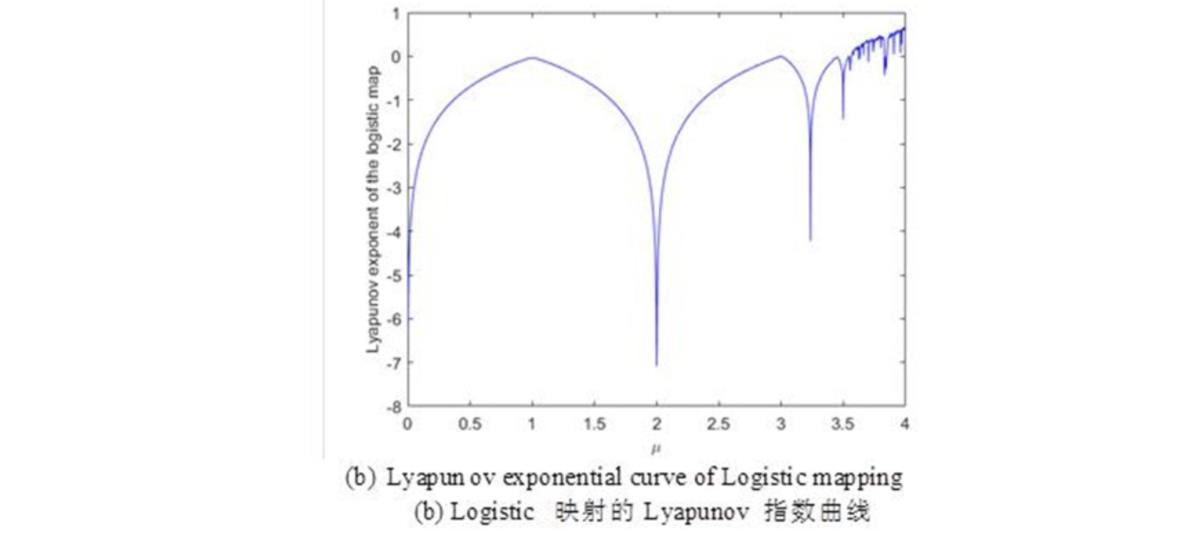
图2 Logistic映射
从图2(a)可知，Logistic映射在μ=3.55左右的位置进行分岔，随着参数取值的增加，映射的范围逐渐增至(0,1)。当μ=4时，Logistic映射的映射序列为(0,1)，其对应的最大Lyapunov指数为0.6839。

HPSBA中控制参数c的表达式为：

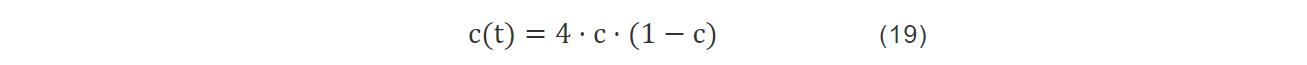
惯性权重系数ω对PSO算法的粒子飞行速度有着直接的影响，能够调整算法的全局搜索和局部搜索能力。本文采用自适应的调整策略为：

针对控制参数c和ω，取Tmax=500，c(0)=0.35，迭代曲线如图3所示，其中c0表示式(9)的控制策略，c表示Logistic映射的控制策略。由图3可知，随着迭代次数的增加，控制参数c0的变化范围在(0, 0.3)；改进的控制策略c则在迭代次数内的取值范围为(0,1)；自适应的调整策略ω由0.9以线性递减至0.2。改进的控制策略能有效调节混合算法的局部搜索和全局搜索，进而寻优到最佳值。

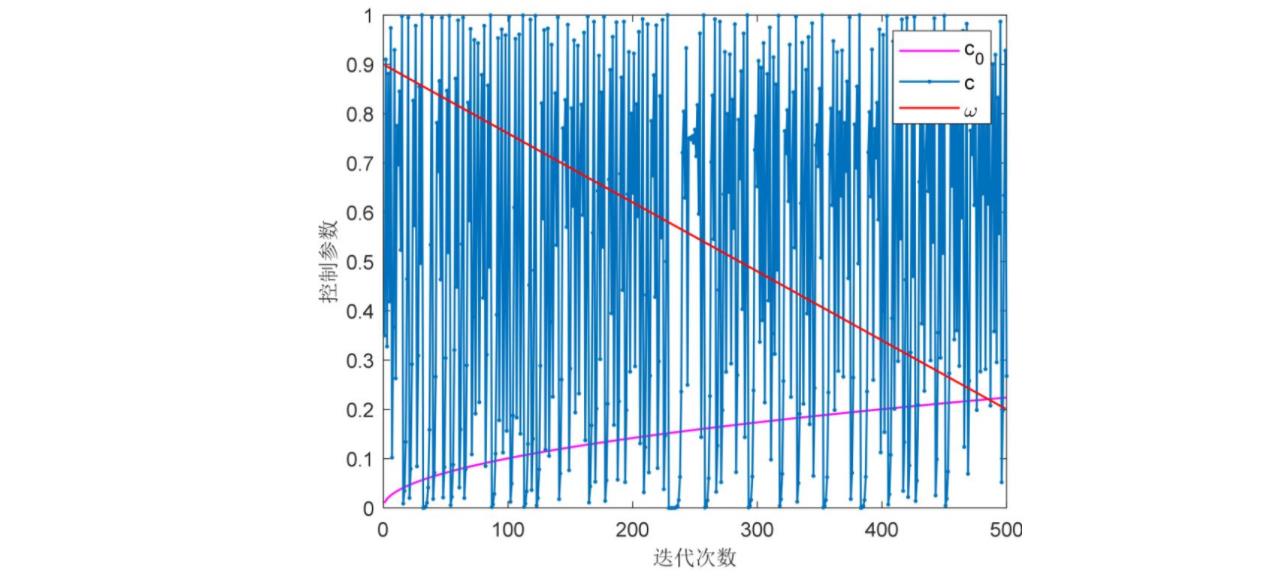
图3 控制参数的变化曲线

二、部分源代码

%___________________________________________________________________________________________ %
%  The HPSOBOA source codes v2.0                                                                 %
                                                          %                                                                                              %
%___________________________________________________________________________________________ %

clear
clc
close all
warning off all

SearchAgents_no = 30;  % Number of search agents
Max_iteration = 500;   % Maximum number of iterations

Function_name='F3';  %F1-F15,US(Unimodal Separable);F16-F26,MS(Multimodal Separable)
%%% Exp2: F1,F2,F4, F6, F15, F17 ,F18
%US: F1,F2,F4,F6,F11, MS: F15, F17, F18, F24, F25

%%%%%  BOA in 2018
[lb,ub,dim,fobj]=Hight_Get_Functions_details(Function_name);
[Best_scoreBOA,Best_pos,BOA_cg_curve]=BOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);

%%%% PSOBOA in 2020
[Best_score_PSOBOA,Best_pos_PSOBOA,PSOBOA_cg_curve]=PSOBOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);

%%%% HPSOBOA in 2020
[Best_score_HPSOBOA,Best_pos_HPSOBOA,HPSOBOA_cg_curve]=HPSOBOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);

%%%% plots
figure('Position',[500 400 800 200])  %[left bottom width height]
subplot(1,2,1);
func_plot_con(Function_name);
title(Function_name)
% xlabel('x_1');
% ylabel('x_2');
% zlabel([Function_name,'( x_1 , x_2 )'])

%%%%%% Convergence curves 
subplot(1,2,2);
semilogy(BOA_cg_curve,'b-','LineWidth',1)
hold on
semilogy(PSOBOA_cg_curve,'g-','LineWidth',1)
hold on
semilogy(HPSOBOA_cg_curve,'r-','LineWidth',1)

% axis tight
% grid off
xlabel('Iterations');
ylabel('Fitness value');
legend('BOA','PSOBOA','HPSOBOA')
%___________________________________________________________________%
%  The benchmark functions of hight dimension                       %
%                                                                   %
%  Developed in MATLAB R2018a(7.30)                                 %
%                                                                   %
                             %
%___________________________________________________________________%

% lb is the lower bound: lb=[lb_1,lb_2,...,lb_d]
% up is the uppper bound: ub=[ub_1,ub_2,...,ub_d]
% dim is the number of variables (dimension of the problem)

function [lb,ub,dim,fobj] = Hight_Get_Functions_details(F)
d=100;   %%%dim=30,100

switch F
    case 'F1'
        fobj = @F1;
        lb=-100;
        ub=100;
        dim=d;
        
    case 'F2'
        fobj = @F2;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F3'
        fobj = @F3;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F4'
        fobj = @F4;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F5'
        fobj = @F5;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F6'
        fobj = @F6;
        lb=-1.28;
        ub=1.28;
        dim=d;
        
    case 'F7'
        fobj = @F7;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F8'
        fobj = @F8;
        lb=-1;
        ub=1;
        dim=d;
        
    case 'F9'
        fobj = @F9;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F10'
        fobj = @F10;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F11'
        fobj = @F11;
        lb=-5.12;
        ub=5.12;
        dim=d;
        
    case 'F12'
        fobj = @F12;
        lb=-5;
        ub=5;
        dim=d;
        
    case 'F13'
        fobj = @F13;
        lb=-100;
        ub=100;
        dim=d;
        
    case 'F14'
        fobj = @F14;
        lb=-100;
        ub=100;
        dim=d;
        
    case 'F15'
        fobj = @F15;
        lb=-10;
        ub=10;
        dim=d;
        
    case 'F16'
        fobj = @F16;
        lb=-5.12;
        ub=5.12;
        dim=d;
        
    case 'F17'
        fobj = @F17;
        lb=-5.12;
        ub=5.12;
        dim=d;
        
    case 'F18'
        fobj = @F18;
        lb=-20;
        ub=20;
        dim=d;
        
    case 'F19'
        fobj = @F19;
        lb=-600;
        ub=600;
        dim=d;
        
    case 'F20'
        fobj = @F20;
        lb=-10;
        ub=10;
        dim=d;     
        
    case 'F21'
        fobj = @F21;
        lb=-10;
        ub=10;
        dim=d;    
        
    case 'F22'
        fobj = @F22;
        lb=-5;
        ub=5;
        dim=d;    
        
    case 'F23'
        fobj = @F23;
        lb=-2;
        ub=2;
        dim=d;  
           
    case 'F24'
        fobj = @F24;
        lb=-1;
        ub=1;
        dim=d; 
            
    case 'F25'
        fobj = @F25;
        lb=-20;
        ub=20;
        dim=d; 
           
    case 'F26'
        fobj = @F26;
        lb=-5;
        ub=5;
        dim=d; 
end
end

三、运行结果

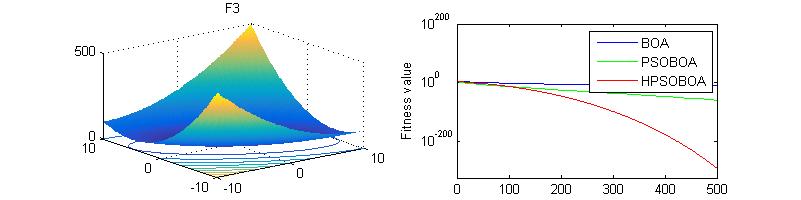
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.