- 第六节：概率

Posted 2022-05-10 海轰Pro

目录

• 前言
• 2.6. 概率
• • 2.6.1. 模拟扔骰子
  • 2.6.2. 处理多个随机变量
  • • 2.6.2.1. 联合概率
    • 2.6.2.2. 条件概率
    • 2.6.2.3. 贝叶斯定理
    • 2.6.2.4. 边际化
  • 2.6.3. 期望和方差
• 结语
• 参考文献

前言

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 

知其然 知其所以然！

 
本文仅记录自己感兴趣的内容

2.6. 概率

2.6.1. 模拟扔骰子

1. 导包

%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l

2. 生成一个多项式分布，再采样

fair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample()

# tensor([1., 0., 0., 0., 0., 0.])

解释：torch.distributions.multinomial.Multinomial()

---

fair_probs = torch.ones([6]) / 6 理解为生成一个向量，其中概率都为1/6，对应扔数字1-6概率都为1/6

multinomial.Multinomial(1, fair_probs)理解为依据fair_probs这个概率向量，实验一次（扔一次骰子）

multinomial.Multinomial(1, fair_probs).sample()就是再multinomial.Multinomial(1, fair_probs)的基础上进行采样（看看具体扔出的数字是哪一个）

---

# 将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000  # 相对频率作为估计值

# tensor([0.1550, 0.1810, 0.1760, 0.1830, 0.1480, 0.1570])

counts = multinomial.Multinomial(1000, fair_probs).sample()表示，依据概率fair_probs，扔1000次骰子，再统计每个数字扔出的次数

上图中数字1扔出了187次，数字2扔出了145次…

counts / 1000也就是求1000次实验中每个数字被扔出的概率

---

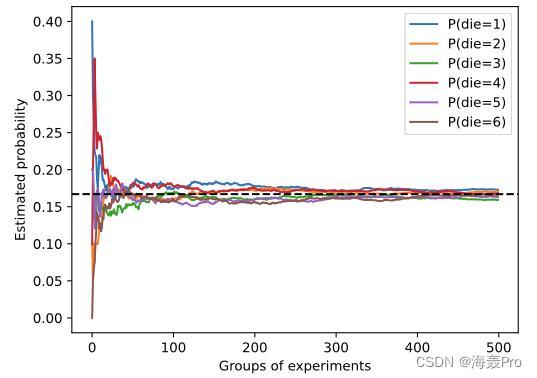
3. 绘图

counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)

d2l.set_figsize((6, 4.5))
for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),
                 label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();

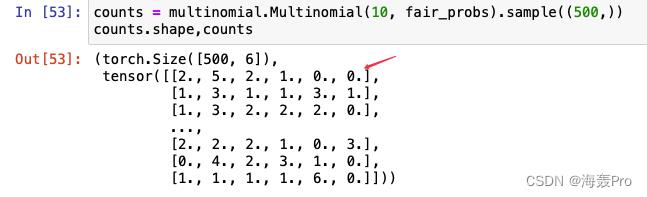
counts = multinomial.Multinomial(10, fair_probs).sample((500,))理解为以概率fair_probs进行10次实验，生成一个多项式分布，然后再此基础上，采样500次（相当于进行了500组实验，每组需要扔10次骰子）

---

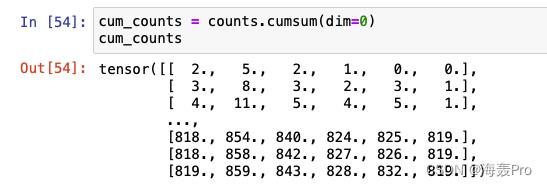
cum_counts = counts.cumsum(dim=0)：进行累加（按照行进行累加，第二行=第二行 + 第一行…）

---

cum_counts.sum(dim=1, keepdims=True)，对每一行进行求和

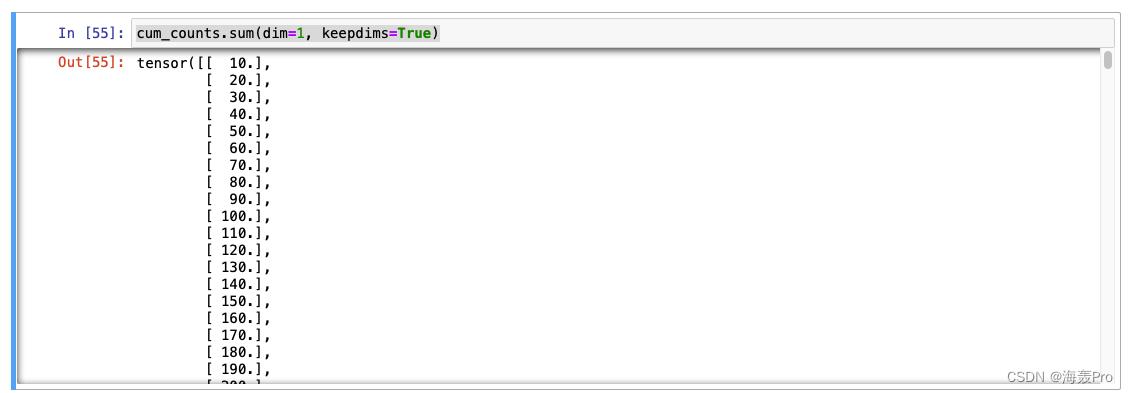
如果没有参数keepdims=True，则为

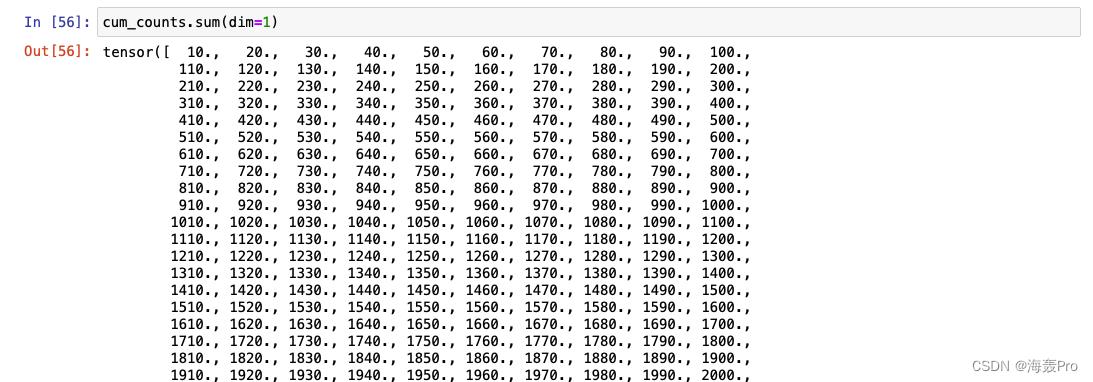
简单的说，就是keepdims=True后，可以使得结果维度与原来数据保持一致（注意下图中的中括号！）

---

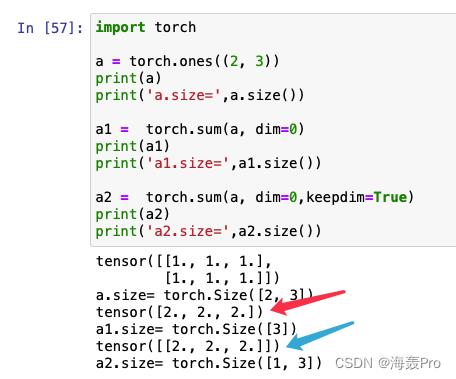
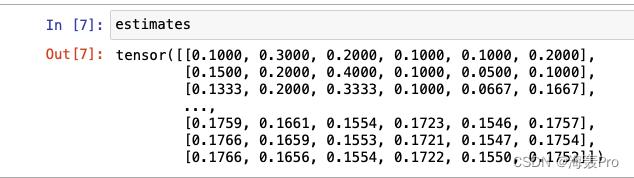
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)

2.6.2. 处理多个随机变量

2.6.2.1. 联合概率

2.6.2.2. 条件概率

2.6.2.3. 贝叶斯定理

$P(A,B)$是指同时为$A、B$的概率

由公式

• $P(A,B)=P(B|A)P(A)$
• $P(A,B)=P(A|B)P(B)$

推出

• $P(B|A)P(A)=P(A|B)P(B)$

将$P(B)$移项得

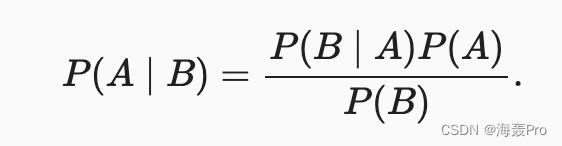
2.6.2.4. 边际化

2.6.3. 期望和方差

结语

学习资料：http://zh.d2l.ai/

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正

参考文献

• https://blog.csdn.net/weixin_42179158/article/details/123097338
• https://zhuanlan.zhihu.com/p/268162211