深度学习经典网络解析:LeNet-5
Posted Jsper0420
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习经典网络解析:LeNet-5相关的知识,希望对你有一定的参考价值。
深度学习经典网络解析(一):LeNet-5
1.背景介绍
LeNet-5,这篇是由LeCun和Bengio在1998年撰写的论文(LeCun和Bengio和Hitton成被称为深度学习三巨头,在2018年一起获得图灵奖)。LeNet-5创造了卷积神经网络(Convolutional Neural Networks, CNN),基本上为CNN在2012年以后的爆发奠定了基调。当初LeNet-5的设计主要是为了帮美国邮政局解决手写识别支票的问题。那时传统的识别方案很多特征都是hand-crafted,识别的准确率很大程度上受制于所设计的特征,而且最大的问题在于手动设计特征对领域性先验知识的要求很高还耗时耗力,更别谈什么泛化能力,基本上只能针对特定领域。现在在美国,给别人付钱,大部分是写一个check,就下面这个东西
在在美国邮政局是一个非常非常大的一个机构,他现在的地位越来越低了,这个邮政局反正这个是算政府部门,然后是一个特别重要的一个部门,所以当年他确实是有很大的话语权呢,你像美国选举这个需要通过邮政局投票。然后这个模型确实在80年代末期在银行行业,在邮递行业确实是被一直被应用,所以这也是为什么LeNet-5有名。
2.LeNet-5网络架构
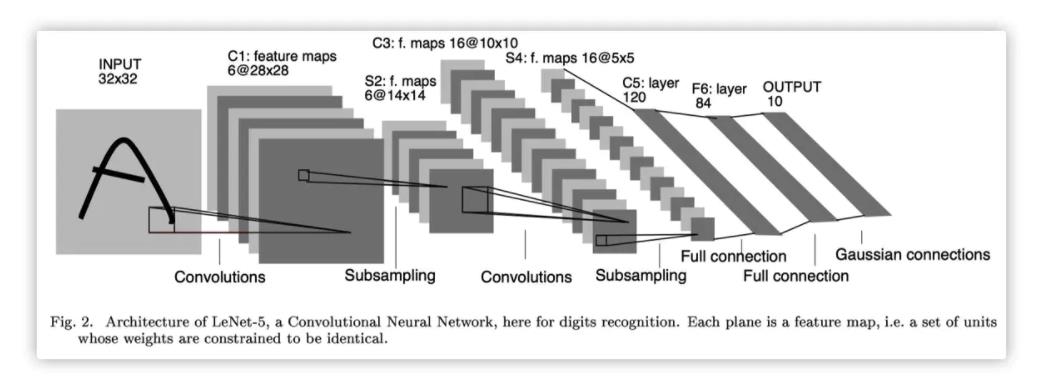
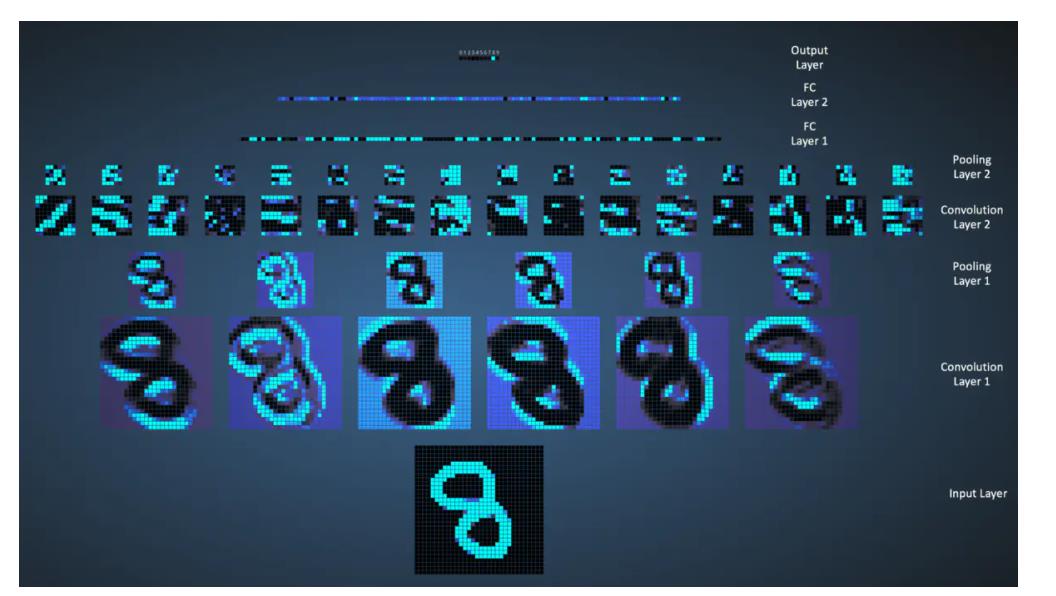
LeNet每一层执行的效果如下:
2.1输入层
首先通过尺寸归一化,把输入图像全部转化成32×32大小。
2.2第一层-卷积层C1
在介绍LeNet网络时,我们首先要了解图像是如何在网络中表示的。在LeNet网络中,输入图像是手写字符,图像的表示形式为二维数据矩阵,如下图所示:

LeNet网络总共有六层网络(不包含输入输出层)。第一层是卷积层(图中C1层):
-
输入图像的大小为32×32
-
卷积核kernel size的大小为5×5
-
卷积核数量为6个
-
输出featuremap大小:28×28 (28通过32-5+1计算得到,公式详情百度原理)
-
神经元数量:28×28×6
-
训练参数:(5×5+1)×6=156 由于参数(权值)共享的原因,对于同个卷积核每个神经元均使用相同的参数,因此,参数个数为(5×5+1)×6= 156,其中5×5为卷积核参数,1为偏置参数.
-
连接数:训练参数×输出featuremap大小=(5×5+1)×6×28×28=122304
卷积的作用主要是:通过卷积运算,可以使原信号特征增强,降低噪音。在图像上卷积之后主要是减少图像噪声,提取图像的特征。
卷积网络能很好地适应图像的平移不变性:例如稍稍移动一幅猫的图像,它仍然是一幅猫的图像。卷积操作保留了图像块之间的空间信息,进行卷积操作的图像块之间的相对位置关系没有改变。
图像在不同卷积核上进行卷积之后的效果图如下:

卷积操作如下面两幅图所示: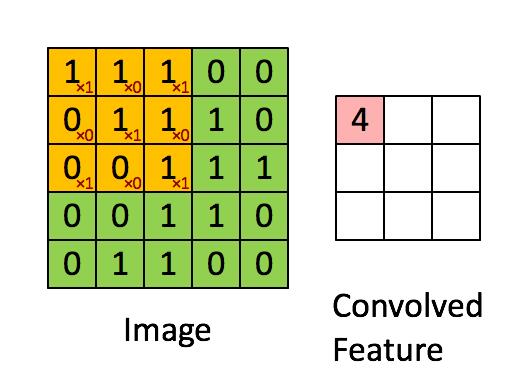

2.3第二层-池化层S2(下采样)
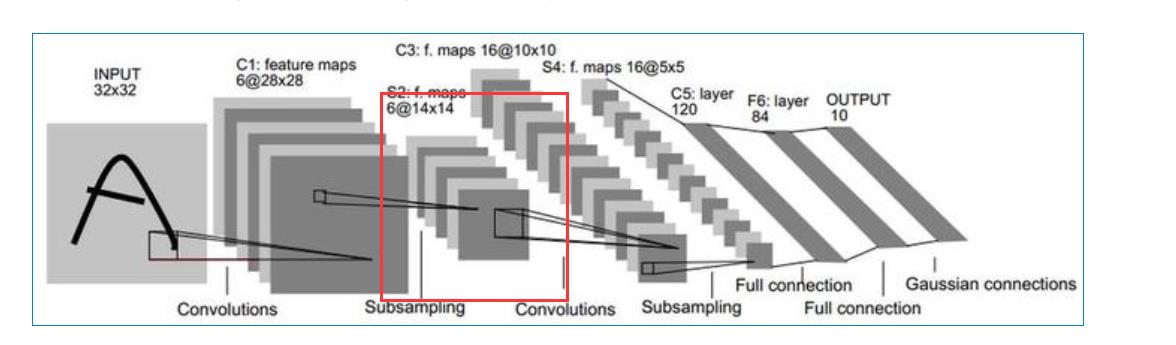
-
池化层的输入大小:28×28
-
池化大小:2×2
-
池化层数:6
-
输出featureMap大小:14×14
-
神经元数量:14×14×6
-
训练参数:2×6
-
连接数:(2×2+1)×6×14×14
池化层的作用是特征映射(特征降维)。如果池化单元为2×2,6个特征图的大小经池化后从28×28变为14×14。为什么池化后大小减半?因为在本文的池化单元之间没有重叠(有的时候池化单元会重叠),在池化区域内进行聚合统计后得到新的特征值,因此经2×2池化后,每两行两列重新算出一个特征值出来,相当于图像大小减半,因此卷积后的28×28图像经2×2池化后就变为14×14。
池化层的计算过程:2×2 单元里的值相加,然后再乘以训练参数w,再加上一个偏置参数b(每一个特征图共享相同的w和b),然后取sigmoid值(S函数:0-1区间),作为对应的该单元的值。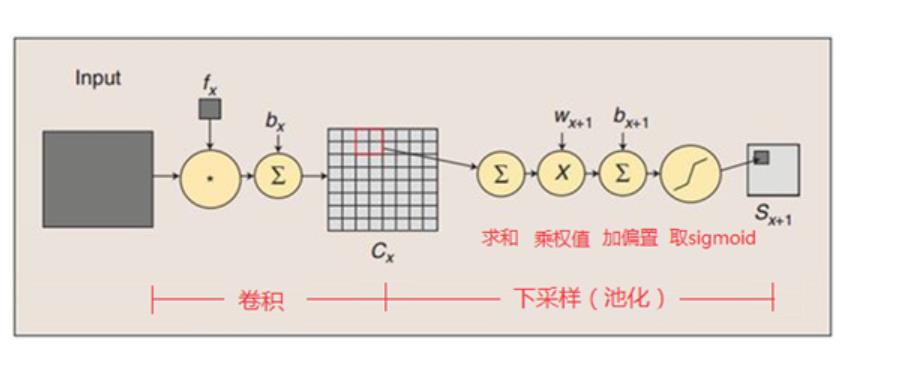
池化示意图如下:
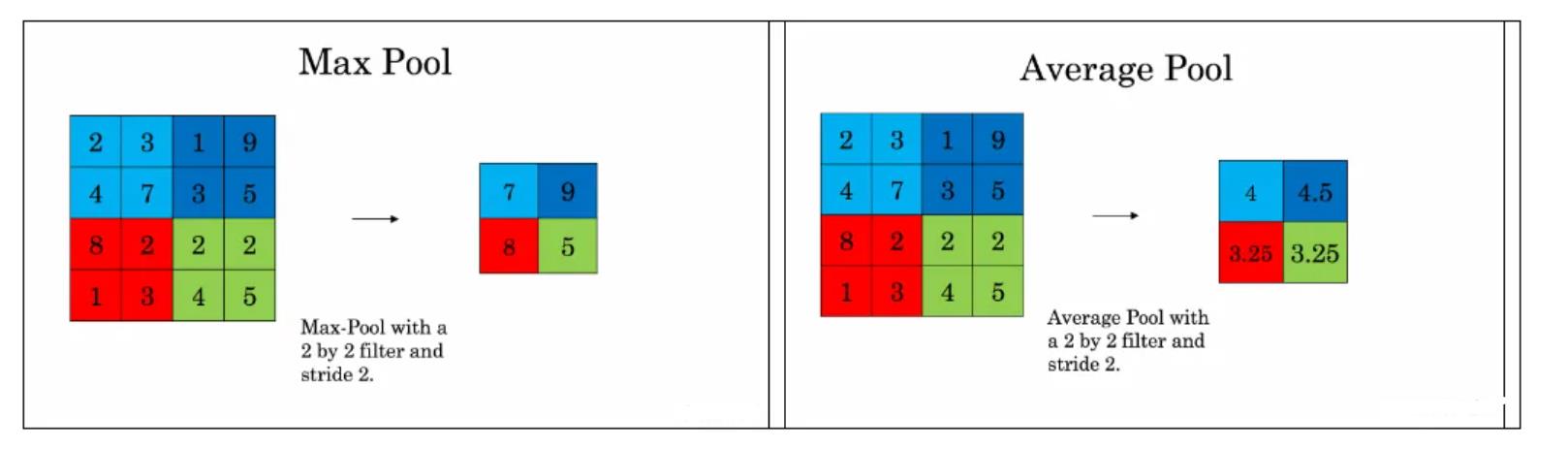
2.3第三层-卷积层C3
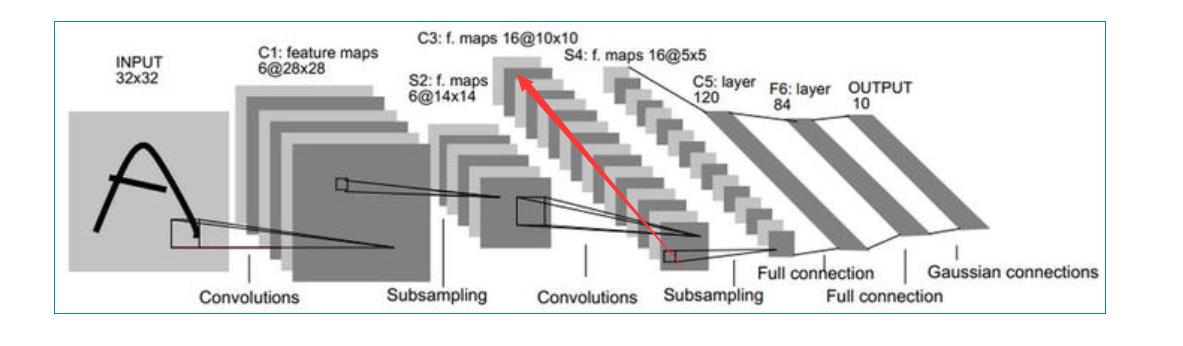
-
卷积层C3输入:S2中6个特征图组合
-
卷积核大小:5×5
-
卷积核个数:16
-
输出featureMap大小:10×10 (14-5+1)=10
-
训练参数:6×(3×5×5+1)+6×(4×5×5+1)+3×(4×5×5+1)+1×(6×5×5+1)=1516(计算原理见额外处理)
-
连接数:10×10×1516=151600
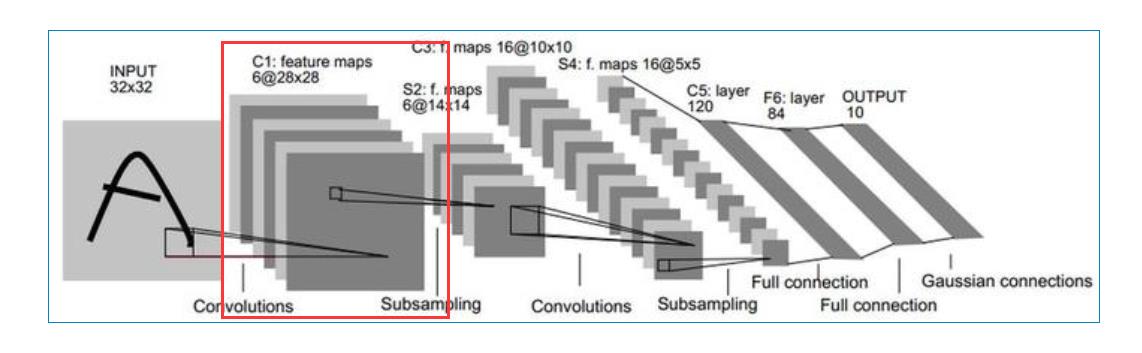
第三层的输入为14×14的6个feature map,卷积核大小为5×5,因此卷积之后输出的feature map大小为10×10。但是由于卷积核有16个,所以希望输出的feature map也为16个,但由于输入只有6个feature map,因此需要进行额外的处理。输入的6个feature map与输出的16个feature map的关系图如下:
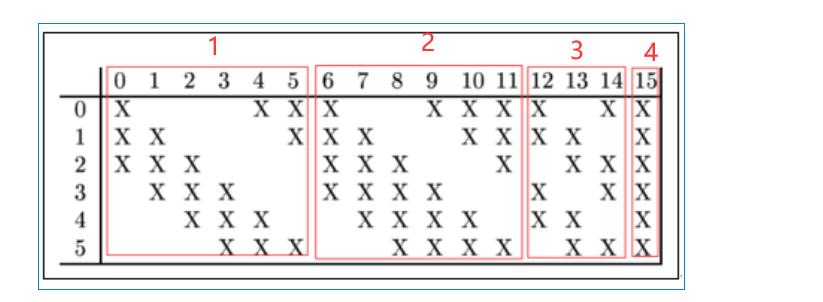
额外处理:
C3的前6个feature map(上图红框1的6列)与S2层相连的3个feature map相连接(上图红框1的某相邻的3行),后面6个feature map(上图红框2的6列)与S2层相连的4个feature map相连接(上图红框2的某相邻的4行),后面3个feature map(上图红框3的3列)与S2层部分不相连的4个feature map(上图红框3的某不相邻的4行)相连接,最后一个(上图红框4)与S2层的所有feature map(上图红框4的所有行)相连。
第四层-池化层S4
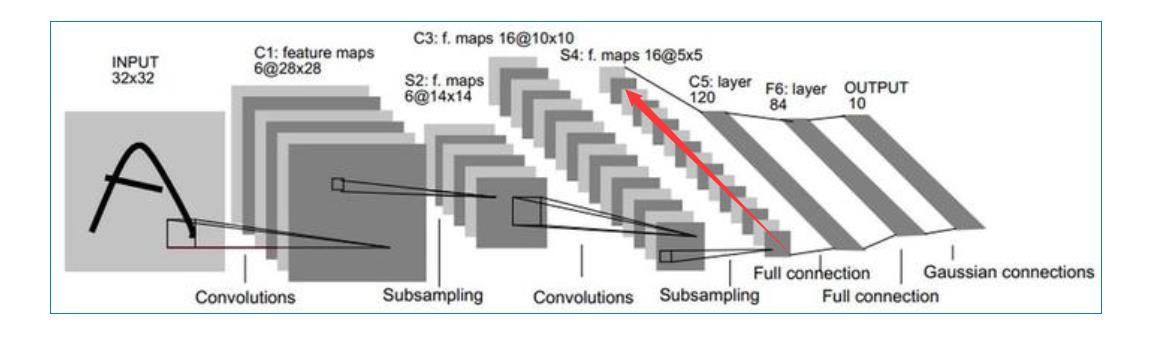
操作S2的类似
- 输入:上一次C3的输出10×10特征图
- 池化大小:2×2
- 池化个数:16
- 输出featureMap大小:**5×5 **
- 神经元数量:5×5×16=400
- 可训练参数:2×16=32
- 连接数:16×(2×2+1)×5×5=2000
第五层-卷积层C5

- 输入:S4层的全部16个5×5特征图
- 卷积核大小:5×5
- 卷积核种类:120
- 输出featureMap大小:1×1(通过5-5+1=1得到)
- 可训练参数/连接:120×(16×5×5+1)=48120
卷积核数目为120个,大小为5×5,由于第四层输出的特征图大小为5×5,因此第五层也可以看成全连接层,输出为120个大小为1×1的特征图。
第六层-全连接层F6
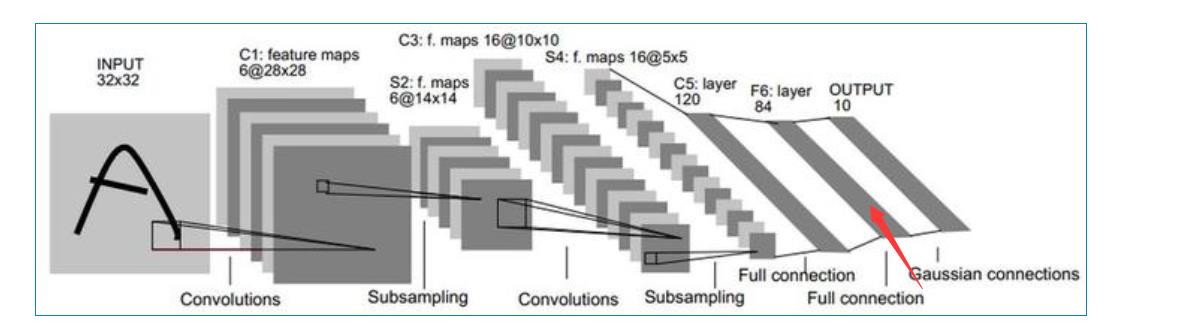
- 输入:上一层C5输出的120维1×1的向量
- 输出大小:84
- 训练参数数目:(120+1)×84=10164
- 连接数:(120+1)×84=10164
第六层是全连接层。F6层有84个节点,对应于一个7x12的比特图,-1表示白色,1表示黑色,这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是(120 + 1)x84=10164。
输出层-Output层
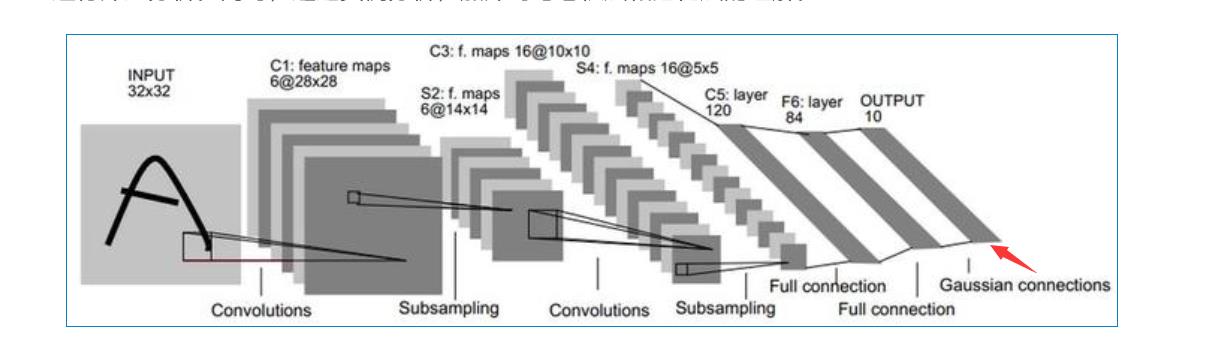
Output层也是全连接层,共有10个节点,分别代表数字0到9。如果第i个节点的值为0,则表示网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式。假设x是上一层的输入,y是RBF的输出,则RBF输出的计算方式是:
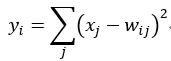
这公式是什么意思呢?
首先我们应该明白径向基神经网络:它基于距离进行衡量两个数据的相近程度的,RBF网最显著的特点是隐节点采用输人模式与中心向量的距离(如欧氏距离)作为函数的自变量,并使用径向基函数(如函数)作为激活函数。径向基函数关于N维空间的一个中心点具有径向对称性,而且神经元的输人离该中心点越远,神经元的激活程度就越低。上式是基于欧几里得距离,怎么理解那个式子呢?就是说F6层为84个输入用表示X_i,输出有10个用表示y_i,而权值W_ji使用,上式说明所有输入和权值的距离平方和为依据判断,如果越相近距离越小,输出越小则去哪个,如果我们存储的到W_ji的值为标准的输出.
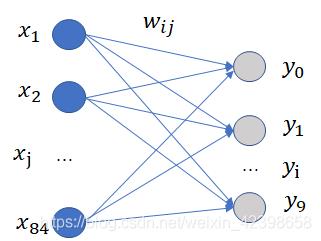 如标准的手写体0,1,2,3等,那么最后一层就说明。F6层和标准的作比较,和标准的那个图形越相似就说明就越是那个字符的可能性更大。我们看看标准的是什么样的:
如标准的手写体0,1,2,3等,那么最后一层就说明。F6层和标准的作比较,和标准的那个图形越相似就说明就越是那个字符的可能性更大。我们看看标准的是什么样的:

上图标准的每个字符都是像素都是12x7=84。这就是解释了为什么F6层的神经元为84个,因为他要把所有像素点和标准的比较在进行判断,因此从这里也可以看出,这里不仅仅可以训练手写体数字,也可以识别其他字符。
3.LeNet-5识别数字3的过程
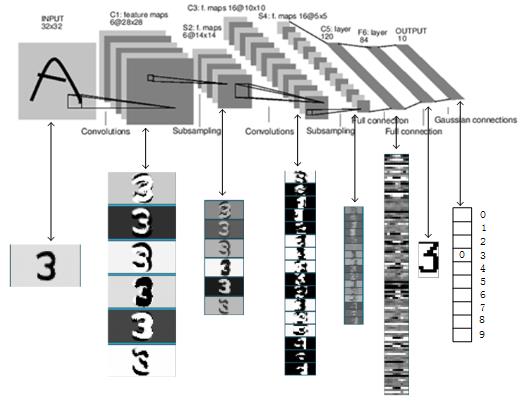
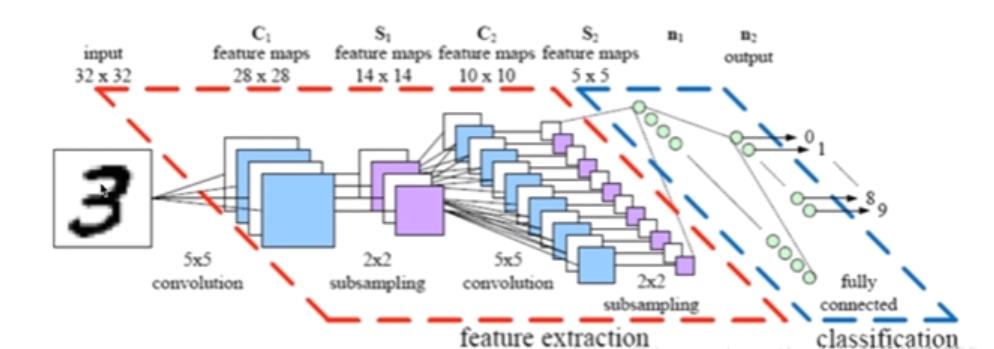
以上是关于深度学习经典网络解析:LeNet-5的主要内容,如果未能解决你的问题,请参考以下文章
(机器学习深度学习常用库框架|Pytorch篇)第(待定)节:卷积神经网络CNN中一些经典网络结构写法