[机器学习与scikit-learn-32]：算法-回归-普通线性模型拟合非线性分布数据-分箱

Posted 2022-03-21 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123562666

---

目录

前言：

第1章 分箱机制

分箱的本质： 用多个线段替代一个直线对目标样本数据进行拟合

第2章 代码实现 

2.1 导入库

2.2 创建非线性分布的数据集

2.3 用原始数据集进行模型训练

2.4 分箱的基本原理

2.5 分箱数据预处理建模

2.6 用分箱后的数据进行线性模型拟合（10个箱子）

2.7 不同箱子对线性模型拟合效果的影响（5个箱子做比较）

2.8 如何动态评估不同箱子效果

---

前言：

普通线性模型拟合非线性分布数据的问题是：线性拟合只有一根直线，导致拟合非线性数据是出现误差较大的情况，如下图所示：

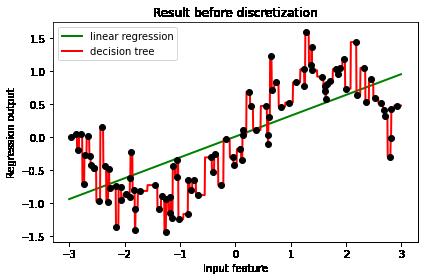
第1章 分箱机制

为了解决线性函数在整个样本空间沿着线性曲线单调增加或单调较小的缺陷，我们使用N个线段替代单一直线进行线性拟合，得到如下的右图示意图。

（1）用20根线段替代单一直线

 （2）用5根线段替代单一直线

很显然，替代后，线性拟合出来的不在是单一直线，而是一个个阶梯型线段，这个线段比单一的直线，更加解决非线性数据分布。上述的思想就是分箱的思想。

分箱的本质是：

（1）属于数据预处理

（2）它对样本数据进行预处理，把连续的样本数据分成N个离散的等级（分段），因变量不在连续。

（3）由于是线性拟合，因此预测结果也不在连续，而是M个离散值，M不一定等于N, 就如上图中的梯形，不是单调增，也不是单调减。

分箱的本质： 用多个线段替代一个直线对目标样本数据进行拟合

第2章 代码实现 

2.1 导入库

# 1. 导入所需要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor

2.2 创建非线性分布的数据集

# 2. 创建需要拟合的数据集
rnd = np.random.RandomState(42) #设置随机数种子
X = rnd.uniform(-3, 3, size=100) #random.uniform，从输入的任意两个整数中取出size个随机数
#生成y的思路：先使用NumPy中的函数生成一个sin函数图像，然后再人为添加噪音
y = np.sin(X) + rnd.normal(size=len(X)) / 3 #random.normal，生成size个服从正态分布的随机数

#使用散点图观察建立的数据集是什么样子
plt.scatter(X, y,marker='o',c='k',s=20)
plt.show()

#为后续建模做准备：sklearn只接受二维以上数组作为特征矩阵的输入
print(X.shape)
X = X.reshape(-1, 1)
print(X.shape)

2.3 用原始数据集进行模型训练

（1）训练模型

# 3.1 使用原始数据训练模型
LinearR = LinearRegression()
LinearR = LinearR.fit(X, y)

TreeR = DecisionTreeRegressor(random_state=0)
TreeR = TreeR.fit(X, y)

（2）展示结果

#3.2 显示原始训练模型效果
# 放置画布
fig, ax1 = plt.subplots(1)
#创建测试数据：一系列分布在横坐标上的点
line_X = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)

#将测试数据带入predict接口，获得模型的拟合效果并进行绘制
ax1.plot(line_X, LinearR.predict(line_X), linewidth=2, color='green', label="linear regression")
ax1.plot(line_X, TreeR.predict(line_X), linewidth=2, color='red', label="decision tree")
#将原数据上的拟合绘制在图像上
ax1.plot(X[:, 0], y, 'o', c='k')
#其他图形选项
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")
plt.tight_layout()
plt.show()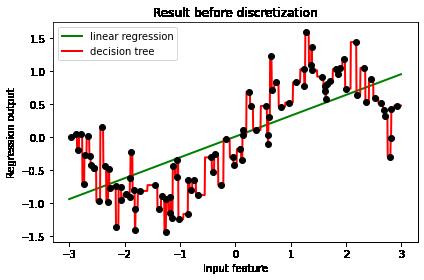

2.4 分箱的基本原理

（1）分箱

# 4 分箱的基本原理
from sklearn.preprocessing import KBinsDiscretizer

#将数据分箱
#encode模式"onehot"：使用做哑变量方式做离散化
#之后返回一个稀疏矩阵(m,n_bins)，每一列是一个分好的类别
#对每一个样本而言，它包含的分类（箱子）中它表示为1，其余分类中它表示为0
enc = KBinsDiscretizer(n_bins=10          # 分10个箱子
                       ,encode="ordinal")  # 
X_binned = enc.fit_transform(X)
print("X.min=", X.min())
print("X.max=", X.max())
print("X.shape=", X.shape)
print("X.X_binned=", X_binned.shape)
print("X的前5个数据:\\n", X[0:5])
print("X_binned的前5个数据:\\n",X_binned[0:5])

X.min= -2.9668672972583856
X.max= 2.9213216196031038
X.shape= (100, 1)
X.X_binned= (100, 1)
X的前5个数据:
 [[-0.75275929]
 [ 2.70428584]
 [ 1.39196365]
 [ 0.59195091]
 [-2.06388816]]
X_binned的前5个数据:
 [[4.]
 [9.]
 [7.]
 [6.]
 [2.]]

（2）分箱的基本工作方式

# 4 分箱的基本工作方式
from sklearn.preprocessing import KBinsDiscretizer

#将数据分箱
#encode模式"onehot"：使用做哑变量方式做离散化
#之后返回一个稀疏矩阵(m,n_bins)，每一列是一个分好的类别
#对每一个样本而言，它包含的分类（箱子）中它表示为1，其余分类中它表示为0
enc = KBinsDiscretizer(n_bins=10          # 分10个箱子
                       ,encode="onehot")  #ordinal
X_binned = enc.fit_transform(X)
print("X.min=", X.min())
print("X.max=", X.max())
print("X.shape=", X.shape)
print("X.X_binned=", X_binned.shape)
print("X的前5个数据:\\n", X[0:5])
print("X_binned的前5个数据:\\n",X_binned[0:5])
# X_binned数据格式：
# 第一列：序号
# 第二列：onehot的编码位置
# 第三列：onehot的编码值

#使用pandas打开稀疏矩阵
import pandas as pd
pd.DataFrame(X_binned.toarray()).head()

X.min= -2.9668672972583856
X.max= 2.9213216196031038
X.shape= (100, 1)
X.X_binned= (100, 10)
X的前5个数据:
 [[-0.75275929]
 [ 2.70428584]
 [ 1.39196365]
 [ 0.59195091]
 [-2.06388816]]
X_binned的前5个数据:
   (0, 4)	1.0
  (1, 9)	1.0
  (2, 7)	1.0
  (3, 6)	1.0
  (4, 2)	1.0

Out[23]:

	0	1	2	3	4	5	6	7	8	9
0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0
1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0
2	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0
3	0.0	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0
4	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0

2.5 分箱数据预处理建模

分箱不属于拟合，而是数据预处理！！

# 5. 使用分箱数据进行建模和绘图

# 定义分箱对象
enc = KBinsDiscretizer(n_bins=10,encode="onehot")
#enc = KBinsDiscretizer(n_bins=10,encode="ordinal")

# 对输入样本进行等级分箱，分箱后，输入样本不在是连续量，而是离散量。
X_binned = enc.fit_transform(X)

line_binned = enc.transform(line_X)  # 分箱后，X轴数据被分割成10个段，即10个箱子。
print(line_X.shape)
print(line_binned.shape)
print("line_X.min=", line_X.min())
print("line_X.max=", line_X.max())
print("line_X.shape=", line_X.shape)
print("line_binned=", X_binned.shape)
print("line_X的前5个数据:\\n", line_X[0:5])
print("line_binned的前5个数据:\\n",line_binned[0:5])  # 分箱后的X不再连续

(1000, 1)
(1000, 10)
line_X.min= -3.0
line_X.max= 2.9939999999999998
line_X.shape= (1000, 1)
line_binned= (100, 10)
line_X的前5个数据:
 [[-3.   ]
 [-2.994]
 [-2.988]
 [-2.982]
 [-2.976]]
line_binned的前5个数据:
   (0, 0)	1.0
  (1, 0)	1.0
  (2, 0)	1.0
  (3, 0)	1.0
  (4, 0)	1.0

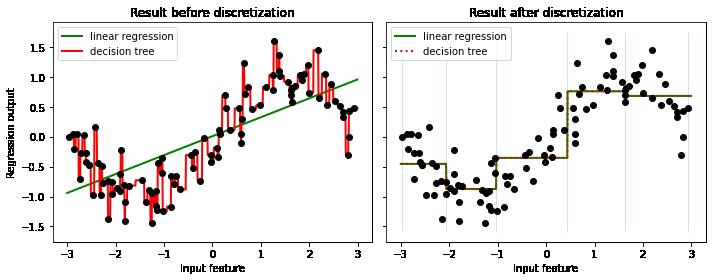
2.6 用分箱后的数据进行线性模型拟合（10个箱子）

#将两张图像绘制在一起，布置画布
fig, (ax1, ax2) = plt.subplots(ncols=2
                               , sharey=True #让两张图共享y轴上的刻度
                               , figsize=(10, 4))

#在图1中布置在原始数据上建模的结果
ax1.plot(line_X, LinearR.predict(line_X), linewidth=2, color='green',label="linear regression")
ax1.plot(line_X, TreeR.predict(line_X), linewidth=2, color='red', label="decision tree")
ax1.plot(X[:, 0], y, 'o', c='k')
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")

#使用分箱数据进行建模
LinearR_ = LinearRegression().fit(X_binned, y)
TreeR_ = DecisionTreeRegressor(random_state=0).fit(X_binned, y)

#进行预测，在图2中布置在分箱数据上进行预测的结果
ax2.plot(line_X #横坐标
         , LinearR_.predict(line_binned) #分箱后的特征矩阵的结果Y, 也不再是连续量，而是离散量。
         , linewidth=2
         , color='green'
         , linestyle='-'
         , label='linear regression')

ax2.plot(line_X, TreeR_.predict(line_binned), linewidth=2, color='red',linestyle=':', label='decision tree')
#绘制和箱宽一致的竖线
ax2.vlines(enc.bin_edges_[0] #x轴
           , *plt.gca().get_ylim() #y轴的上限和下限
           , linewidth=1
           , alpha=.2)

#将原始数据分布放置在图像上
ax2.plot(X[:, 0], y, 'o', c='k')
#其他绘图设定
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")
plt.tight_layout()
plt.show()

#备注：
# 分箱后，线性模型可以拟合非线性数据
# 分箱后，可以克服决策的过拟合

 2.7 不同箱子对线性模型拟合效果的影响（5个箱子做比较）

enc = KBinsDiscretizer(n_bins=5,encode="onehot")

2.8 如何动态评估不同箱子效果

# 7. 如何选取最优的箱数
from sklearn.model_selection import cross_val_score as CVS
import numpy as np
pred,score,var = [], [], []
#binsrange = [2,5,10,15,20,30]
binsrange = list(range(2,30))

for i in binsrange:
    #实例化分箱类
    enc = KBinsDiscretizer(n_bins=i,encode="onehot")
    #转换数据
    X_binned = enc.fit_transform(X)
    line_binned = enc.transform(line_X)
    
    #建立线性模型
    LinearR_ = LinearRegression()
    
    #全数据集上的交叉验证
    cvresult = CVS(LinearR_, X_binned,y,cv=5)
    
    # 记录分数
    score.append(cvresult.mean())
    var.append(cvresult.var())
    #测试数据集上的打分结果
    pred.append(LinearR_.fit(X_binned,y).score(line_binned,np.sin(line_X)))

#绘制随着箱子数目的变化，交叉验证的分数
plt.figure(figsize=(6,5))
plt.plot(binsrange,pred,c="orange",label="test")
plt.plot(binsrange,score,c="k",label="full data")
plt.plot(binsrange,score+np.array(var)*0.5,c="red",linestyle="--",label = "var")
plt.plot(binsrange,score-np.array(var)*0.5,c="red",linestyle="--")
plt.legend()
plt.show()

#备注：
# 1. 从图形可以看出，随着箱子数目的增加，交叉验证的分数在数据上会逐渐增加。
# 2. 但当箱子的数目超过20之后，交叉验证的分数反而是下降的
# 3. 测试集的分数要高于全数据集

mapping = [*zip(pred, binsrange)]
mapping = sorted(mapping,reverse = True)
mapping

[(0.9660434948725315, 19),
 (0.9652516448868957, 21),
 (0.9639830451101487, 24),
 (0.9622614514281138, 12),
 (0.9620400358666081, 14),
 (0.9619989011062795, 23),
 (0.9590978882491229, 15),
 (0.9585720815564842, 18),
 (0.9584114197704767, 26),
 (0.957237960534212, 16),
 (0.9566086751329097, 20),
 (0.9541740734521215, 17),
 (0.9524184920312658, 22),
 (0.9513138137979673, 11),
 (0.9505447185393926, 28),
 (0.950463224130405, 29),
 (0.9486284965918873, 9),
 (0.946414455583129, 13),
 (0.9452817343808607, 25),
 (0.9449968422975642, 27),
 (0.9441330750510549, 10),
 (0.938682004554821, 8),
 (0.9209034773625397, 7),
 (0.9171762233471714, 6),
 (0.8649069759304867, 5),
 (0.8344479728983831, 4),
 (0.8239109278531977, 2),
 (0.7478242248690032, 3)]

备注：

分数排名前三的箱子数目为：19,21,24。

---

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123562666

​