机器学习机器学习入门02 - 数据拆分与测试&算法评价与调整

Posted 2020-11-22 drchuan

0. 前情回顾

上一周的文章中，我们通过kNN算法了解了机器学习的一些基本概念。我们自己实现了简单的kNN算法，体会了其过程。这一周，让我们继续机器学习的探索。

1. 数据集的拆分

上次的kNN算法介绍中，我们只是简单地实现了这样一个算法，并用一组测试数据进行了测试。

然而，在真正的工程应用中，我们设计出的机器学习算法，并不一定非常准确，甚至可能非常不准确。因此我们需要进行测试，如同我们设计好了一个数据结构后，需要使用尽可能涵盖各种情况的参数调用各个操作，并通过一定的方式观察是否符合我们对这种数据结构的预期。机器学习也是一样。

不过，如何对机器学习算法进行高效的测试呢？

这里，我们的方案是：将原始数据集拆分成两部分：训练数据 ( train ) 和测试数据 ( test )。顾名思义，训练数据就是真正提供给机器来进行学习的材料，而测试数据则用来检验算法在训练数据的作用下能否正确给出相应的预测。具体来说，我们将测试数据的指标部分 ( X_test ) 作为输入传给算法，得到的输出 ( y_predict ) 与测试数据的原本的分类标签 ( y_test ) 进行比较，通过其重合的程度来评估算法的好坏。

于是，我们需要一个算法，负责原始数据集的拆分。

1.1 准备工作

在这之前，我们先引入一个sklearn中的模块datasets，并通过以下代码创建一个原始数据集。

1 from sklearn import datasets
2 
3 iris = datasets.load_iris()
4 
5 X = iris.data
6 y = iris.target

我们调用了datasets中的load_iris方法。得到的X和y均为长度为150的数组，X中的元素是float64类型的四元组，y中的元素是int型的整数。输出结果较长，这里不再给出展示，读者可以执行上述代码后自行print(X), print(y)进行观察。

现在，我们准备好了原始数据，不过我们注意到，数据的分布某种程度上是有顺序的，即：标签为0的在最前面，标签为1的在中间，标签为2的则在最后。这也许会影响我们的实验，所以，在拆分之前，我们还要再做一个工作，就是将原始数据的顺序打乱。

值得注意的是，X和y这两个对象是独立的，打乱其中一者的顺序并不能影响另一者。

我们有两种方案：

---

 

方案一：先拼接后分离

代码如下：

1 tempConcat = np.concatenate((X, y.reshape(-1,1)), axis=1)
2 
3 np.random.shuffle(tempConcat)
4 
5 shuffle_X,shuffle_y = np.split(tempConcat, [4], axis=1)

总共调用了4个函数：

1.2.  numpy.concatenate;   reshape

　　这个函数用来将X和y拼接成一个大的矩阵，第一个参数即为要拼接的对象。注意，由于原本X是一个150行 x 4列的矩阵，而y是一个有150一元素的行向量，即1行 x 150列，这样的两个矩阵自然无法拼接，因此，调用了reshape方法对y进行变形。第一个参数表示行数，-1表示自动，第二个参数表示列数，即一列。y.reshape(-1, 1) 则相当于对y做了转置操作。这样一来，tempConcat中存的将是一个150行 x 5列的矩阵。

3. np.random.shuffle

　　将数组中的元素打乱顺序

4. np.split

　　将数组拆分，[4]表示分界点在第4个元素后（或理解为下标为4的元素前）。事实上，可以放置多个分界——如 [1, 3, 4]. 

这样，shuffle_X, shuffle_y 就保存了打乱顺序的X矩阵和y向量，并且它们的对应关系没有被破坏。

---

 

方案二：保留原数组，生成随机索引

稍微解释一下，就是说，我们不对原始数据进行实际的打乱操作，而只是创建一个索引数组，长度与原始数据个数相同，如本例中的150。数组的内容覆盖0~149这150个整数，顺序是混乱的。这样，我们依次访问索引数组中的元素，并将其作为下标，访问原始数据，这样，每一个原始数据都能被访问到，且顺序是随机的（只是随机的次序被索引数组确定）。

创建索引数组只需要一行代码：

shuffle_index = np.random.permutation(len(X))

上面的描述有些抽象，下面展示一下上面这行代码得到的结果，也许可以帮助理解。

我将这段代码运行了三次，分别得到了以下输出：

[ 40  93 138  23  69  84 147   4  85 140  54  95 131 145  15  77 146 104
   2  72 105  22  65  11  50  45  25  42 139  58 142  91 106  56 115  99
  61 119  39   7  74  29 149  35  86 110  55 143  49  87  96  43  28 144
  17 137  47 135 118  67   3 113  71 117   5  66 125  89   6  34  81  10
  88  70 148 132   0  41  78   9  27 121 127 128 133  14  12 114 141 112
  92  59 101  36  94  64 126 122  46  16 102  60 124  83  19  82  73 111
  76 108  62  48  13 129 107  26 103  21  52  63 116  32  38 109  53  37
 130 134  51  31  20 120  57  90   1  18 123  97  68 136  98  33  30  80
  75 100  44  24  79   8]

[ 78  37  13  12  18 131 140 142 148   7  40  87  95  61  41 149  57 132
   1  86 135  71 101  51 143  65  48 117  81  19 146  27  16 102  49 138
 147  79  69  52 141 145 130 105  80  93  72  33 121 100  20 113  21  84
 139 128 129  53  59  82  24  89  74  38  76  36  56 134  73  91 126 137
  96  30  68  85 144 107  34  77  66 124  55  28  75 111  32 133  54  35
  29  50 136  22 127  99   9   8  43  15  90  97  25  14 115   4 114  10
  11 103  70  94  63  92  42  88 108 112  31 125 122  67 119  23  47  83
 123  98   0 110   6 109  58  26  46  45 118  39 116  62  17   5  44  60
 106  64 120 104   2   3]

[ 17  36 113 138  53 100 105  64  77  33  27  65  96  25  54 123 121 106
  57 122   4 120 128 142   8  99  76  12  41  30  61  16 131 111  56  86
 139  68 102  71  44  72  21 141  15  79  83  78  66 126  89  91  63  60
  70  74 110  90  85 143  51  10 101 112  14  35   3  34  37  62  97 136
  55  45 135  80 116  18  84 144  39 137  49 130  88  23 125  95  29  11
  75  24  32 108  40 118 146  87  43 115  81 124 145   7   5  13  20  28
 134 103  38  94 133   9 140   6  98  22 129 147  82  52 149   0  73 107
 132  50  58   2  93  47 127 114  59 117  67 109  69  48 148  92  42  31
   1 119  46  26  19 104]

以最后一次的运行结果为例，假如依次以shuffle_index中的元素作为下标来访问原始数据，将会依次访问第18个，第37个，第114个，...，第105个数据，实现了打乱原始数据的访问顺序的效果。

---

 

下面，我们准备将得到的(X, y)这组原始数据进行拆分。

1.2 拆分

在亲手实现拆分之前，我们不妨先来看一下sklearn库中的拆分函数是什么样子的，然后尝试模仿它的效果。

1 from sklearn.model_selection import train_test_split
2 
3 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

简要分析，函数返回四个列表，分别是X和y的训练部分和测试部分。参数中的test_size表示分配到测试部分的比重，0.2即将原数据集的20%用于测试，80%用于训练。

下面是我们自己对分离算法的实现：

 1 import numpy as np
 2 def train_test_split(X, y, test_ratio=0.2, seed=None):
 3     assert X.shape[0] == y.shape[0], "the size of X must be equal to the size of y"
 4     assert 0.0 <= test_ratio <= 1.0, "test_train must be valid"
 5 
 6     if seed:
 7         np.random.seed(seed) 
 8     shuffle_index = np.random.permutation(len(X))
 9 
10     test_size = int(len(X) * test_ratio)
11     test_index = shuffle_index[:test_size]
12     train_index = shuffle_index[test_size:]
13 
14     X_train = X[train_index]
15     X_test = X[test_index]
16     y_train = y[train_index]
17     y_test = y[test_index]
18     return X_train, X_test, y_train, y_test

我们采用上述的方案2对数据集进行乱序。下面简单分析一下代码。

3, 4行是对参数正确性的检查。6, 7行是决定乱序操作要不要使用随机种子。如果我们在测试算法的正确性，为了每次得到相同的序列，则不传入seed参数，将不使用种子；在正式调用时，为了增强随机性，可以通过为seed参数传值，得到不同的索引序列。

10到12行是对索引数组进行了分离，最后14到17行依据索引数组对原始数据进行了分离。

只要理解了1.1中讲的方案二，整段代码没有什么难以理解的逻辑和语言点，因此不再多作解释。

2. 算法的评估

对一个机器算法进行评估，无非就是判断其预测的正确次数与总的预测次数的关系。值得注意的是，我们并不能粗暴地将正确预测的次数与总共预测的次数的比值作为衡量一切算法的标准，在有的算法里，也许未必一定要求这一指标有多么高，而在另外一些算法里，仅仅这一比值达到99.9%可能也不能达到我们的要求。因此上文中笔者使用了“关系”一词，而不是比值。

刚刚提到的比值，有一个专门的术语，叫作分类准确度。这是最简单的一种评价指标，除此之外还有精度、召回率等更加全面的指标，适用于不同的场景。就如同我们在概率论与数理统计中对样本的统计量有均值、方差，可以反映其整体的一些特性，但在此之上，又有均方误差(MSE)这样更为复杂的指标来作进一步的分析。

下面，我们介绍分类准确度。

分类准确度

我们刚才已经给出了这一概念的解释，即正确预测的数量除以总的预测次数。

我们照例先来看sklearn中提供的分类准确度函数。

1 from sklearn.model_selection import train_test_split
2 from sklearn.metrics import accuracy_score
3 
4 accuracy_score(y_test, y_predict)

即传入y_test和y_predict两个列表，可得到相应的分类准确度。

接下来，我们自己实现分类准确度的计算函数。

1 import numpy as np
2 from math import sqrt
3 
4 def accuracy_score(y_true, y_predict):
5     assert y_true.shape[0] != y_predict.shape[0],  "the size of y_true must be equal to the size of y_predict"
6     return sum(y_true == y_predict) / len(y_true)

这样，就实现了分类准确度的计算。其他的评价指标，本文中暂时不做介绍，在后续的文章中可能会有进一步的研究。

3. 算法的调整

在使用kNN算法时，我们传入了一个参数k。不难理解的一点是，k的选择与算法的实际效果好坏有着紧密的关系。k过小，会容易受到偶然因素的影响而做出误判；k过大，一来增加了时间成本，更重要的是，一些距离较远的点也加入了“投票”，同样可能干扰结果。因此，只有取一个恰到好处的k值，才能保证算法预测的准确度。

这个k值，称为kNN算法的超参数。什么叫超参数？就是对于一个算法而言，调用时需要预先人为指定的、与算法的执行过程有关的参数。当然，这里所说的人为指定，并不是说必须在代码中写明k=5，只是说需要将其显式地传入算法的调用中，而不能从数据本身计算得到。说到这里，就不得不提到与之对应的另一种参数，称为模型参数。诸如正态分布中的均值、方差，泊松分布中的k值。

了解了超参数的含义，那么，如何找到最理想的超参数值呢？

我们可以用一个循环来实现。令超参数取遍所有（合理的）值，分别计算在相应值下的预测准确程度（比如分类准确度的大小），筛选出最优的超参数值。

读者也许会问，假如有两个超参数呢？

例如，在kNN算法中，还有一个之前没有提到的超参数：权重的类型。姑且称为weightType。注意，不是指具体某一些点的权重，而是指在本次算法调用中“使用何种权重类型”，比如我们之前对权重的缺省其实就是uniform类型，即weightType = uniform，另外还可以取distance，即以距离作为权重。

在使用了距离权重时，还有一个可以指定的超参数：p

p表示明可夫斯基距离中的幂，p＝2时即为我们熟悉的欧拉距离，p=1时是我们对名字不怎么熟悉但也经常用到的曼哈顿距离。

（如果读者对线性代数还有些印象，用向量观点来看，其实就是两个向量之差的 p-范数 ）

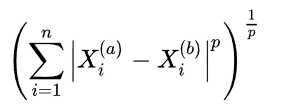
这种情况下，我们只要设计一个双重循环就好了。先遍历k的值，对于k的每一个取值，再遍历weight的值，最终找到最优的组合。

伪代码描述如下：

k_best = k可能最优的范围外的某值
weightType_best = weightType可能最优的范围外的某值
best_score = 0

for ( k in k可能最优的范围 ):
    for ( weightType in weightType可能最优的范围 ):
        t = 以当前k和weightType为参数调用kNN的预测得分
        if ( t > best_score ):
            k_best = k
            weightType_best = weightType
            best_score = t

得到 k_best, weightType_best

最后的最后，新的问题是：如果有好多好多超参数呢？难道要一层循环一层循环地写下去吗？

事实证明，在21世纪，我们能想到的问题，大多都已经有人想到过，并且解决过了（不知道这是幸还是不幸 -_-|||）。sklearn库中提供了这样的一个类GridSearchCV，称为网格搜索。只要将所有我们想要优化的超参数与它们各自的取值范围做成字典，连同用来预测分类的算法相应的分类器对象，传给GridSearchCV类的构造函数，就可以构造网格搜索类的对象了。下面给出一个调用实例：

 1 param_search = [
 2     { "weights":["uniform"], "n_neighbors":[i for i in range(1,11)] },
 3     { "weights":["distance"], "n_neighbors":[i for i in range(1,11)], "p":[i for i in range(1,6)] }
 4 ]
 5 
 6 knn_clf = KNeighborsClassifier()
 7 
 8 from sklearn.model_selection import GridSearchCV
 9 grid_search = GridSearchCV(knn_clf, param_search)
10 grid_search.fit(X_train, y_train)
11 
12 print(grid_search.best_estimator_)

1~4行构造的字典指定了这样的搜索方式：

• 先将weights指定为uniform，即不使用权重，此时，遍历1~11的所有k值；
• 再将weights指定为distance，此时，遍历1~11的 k 和1~6 的 p ，在所有情况中找到最优的组合

返回上述两步中总的最优解。

最后一行即可打印出网格搜索给出的最优结果。具体返回结果的引用可以参阅官方文档中的说明：http://lijiancheng0614.github.io/scikit-learn/modules/generated/sklearn.grid_search.GridSearchCV.html

4.总结

本文第一部分，我们讨论了如何将原始数据集拆分成训练数据和测试数据，从而检验算法的效果。

进一步，在第二部分，我们利用第一部分分离出的数据集进行了算法的评估，利用的是分类准确度这一指标。

最后，有了一种大致可靠和可行的评估的标准和方案的基础上，我们研究了超参数的调整，即根据评价指标的高低，选择各超参数最优的值。

这周的文章就到这里啦~