优先队列(PriorityQueue)

Posted 2023-05-16

参考技术A https://www.jianshu.com/p/94155f9616bf

在数据结构中，普通的队列是先进先出，但有时我们可能并不想有这么固定的规矩，我们希望能有一个带优先级的队列。考虑在现实生活中，一些服务排队窗口会写着“军人依法优先”；送进医院的患者，即便是按顺序到达的，生病更加严重的往往优先级也会更高；还有操作系统中的作业调度也和优先级有关......
于是我们能不能改进队列？使得队列是有一定优先级的，这样能让一些事物和任务的处理变的更加灵活。当然是可以的，最基本的我们可以基于线性结构来实现，考虑基于线性结构的时间复杂度：

1、队列是一种FIFO（First-In-First-Out）先进先出的数据结构，对应于生活中的排队的场景，排在前面的人总是先通过，依次进行。
2、优先队列是特殊的队列，从“优先”一词，可看出有“插队现象”。比如在火车站排队进站时，就会有些比较急的人来插队，他们就在前面先通过验票。优先队列至少含有两种操作的数据结构：insert（插入），即将元素插入到优先队列中（入队）；以及deleteMin（删除最小者），它的作用是找出、删除优先队列中的最小的元素（出队）。

结构\操作 入队 出队
普通线性结构 O(1) O(n)
顺序线性结构 O(n) O(1)
普通线性结构实现的优先队列出队时间复杂度是O(n)，因为出队要拿出最优先的元素，也就是相对最大的元素（注意：大小是相对的，我们可以指定比较规则），从而要扫描一遍整个数组选出最大的取出才行。而对于顺序线性结构的入队操作，入队后可能破坏了原来的有序性，从而要调整当前顺序。
可以看到使用线性结构总有时间复杂度是O(n)的操作，还有没有更好的实现方式呢，当然是有的，这就要来聊一聊堆Heap。

堆严格意义上来说又叫二叉堆（Binary Heap），因为它的结构是一颗完全二叉树，堆一般分为最大堆和最小堆。

堆性质：
结构性：堆是一颗除底层外被完全填满的二叉树，底层的节点从左到右填入，这样的树叫做完全二叉树。即缺失结点的部分一定再树的右下侧。

堆序性：由于我们想很快找出最小元，则最小元应该在根上，任意节点都小于它的后裔，这就是小顶堆（Min-Heap）；如果是查找最大元，则最大元应该在根上，任意节点都要大于它的后裔，这就是大顶堆(Max-heap)。

最大堆：父亲节点的值大于孩子节点的值
最小堆：父亲节点的值小于孩子节点的值

由于是完全二叉树，节点的索引之间有着一定的关系，故我们可以使用数组来存储二叉堆，具体如下：

如果从索引为0开始存储，则父亲和孩子节点的索引关系如下：

当我们需要向一个最大堆添加一条新的数据时，此时我们的堆变成了这样。

此时，由于新数据的加入已经不符合最大堆的定义了。所以我们需要对新加入的数据进行shift up操作，将它放到它应该在的位置。shift up操作时我们将新加入的数据与它的父节点进行比较。如果比它的父节点大，则交换二者。

此时我们就完成了 对新加入元素的shift up操作。

当我们从堆中(也就是优先队列中)取出一个元素时。我们是将堆顶的元素弹出。(只能从堆顶取出)

此时这个堆没有顶了，那么该怎么办呢？我们只需要把这个堆最后一个元素放到堆顶就可以了。

此时我们就完成了弹出一个元素之后的shift down操作。

replace:去除最大元素后，放入一个新元素
实现：可以先extractMax,再add，两次longn操作。
实现:将堆顶的元素替换以后sift down，一次O(logn)操作

将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn),heapify的过程，算法的复杂度为O(n).

heapify:将任意数组整理成堆的形状。
首先将一个数组抽象成一个堆。这个过程，我们称之为heapify。

之后我们找到这个堆中第一个非叶子节点，这个节点的位置始终是数组的数量除以2，也就是索引5位置的27，从这个节点开始，对每一个非叶子的节点,，进行shift down操作。
27比它的子节点51要小，所以交换二者。

接下来我们看索引2位置的20。首先呢，我们需要将20与它两个子节点中较大的51交换。

每个节点堆化的时间复杂度是O(logn)，那 个节点的堆化的总时间复杂度是O(nlogn)。
推导过程
堆化节点从倒数第二层开始。堆化过程中，需要比较和交换的节点个数与这个节点的高度k成正比。

所以 heapify() 时间复杂度是 O(n).
建堆后，数组中的数据是大顶堆。把堆顶元素，即最大元素，跟最后一个元素交换，那最大元素就放到了下标为n的位置。
这个过程有点类似上面的“删除堆顶元素”的操作，当堆顶元素移除之后，把下标n的元素放堆顶，然后再通过堆化的方法，将剩下的n-1个元素重新构建成堆。一直重复这个过程，直到最后堆中只剩下下标为1的元素，排序就完成了。

topk和selectk问题既可以使用快排思想解决，也可以使用优先队列解决。
快排:O(n) 空间O(1)
优先队列:O(nlogk) 空间O(k)
优先队列的有i是，不需要一次性知道所有数据,数据流的方式处理。

.NET 6 优先队列 PriorityQueue

在最近发布的 .NET 6 中，包含了一个新的数据结构，优先队列 PriorityQueue， 实际上这个数据结构在隔壁 Java中已经存在了很多年了, 那优先队列是怎么实现的呢

本文主要介绍了 .NET 6 新增的数据结构优先队列，感兴趣的也可以看一下 PriorityQueue 的源码, 其实就是基于堆这种结构实现的，也展示了入队和出队的堆结构的变化过程

另外需要注意的是，堆这种结构不是稳定的，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作

所以以相同优先级入队的元素并不能保证以相同的顺序出队。

 

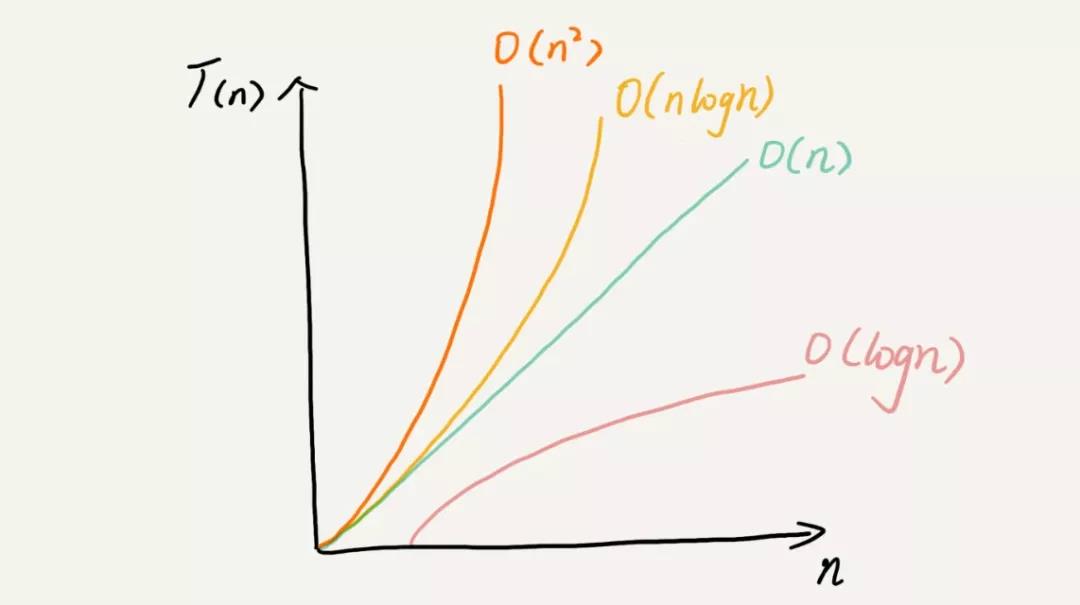
时间复杂度

因为接下来会分析时间复杂度, 这里先贴一张几种时间复杂度的对比图，从低阶到高阶有：O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )。

 

 什么是优先队列

首先，队列大家都知道, 是一个非常基础的数据结构, 它的特点是先进先出（FIFO）。

 

 而优先队列却不一定是先进先出，因为每个元素都有一个权重值, 代表着元素出队的优先级。

 

 队列可以用数组和链表实现, 简单、高效, 这样入队和出队的时间复杂度都是 O(1)。

 

优先队列能不能使用上面的方法呢？也可以, 但是每次新元素入队后, 需要和队列内的元素进行遍历和大小对比, 然后插入到合适的位置, 让整个序列保持从大到小或者从小到大，这样入队的时间复杂度变成 O(n)， 而出队复杂度不变, 还是 O(1)。

O(n) 代表入队的时间是线性增长的, 效率较低, 有没有更高效的方法呢？

 
堆 Heap

堆这种数据结构的应用场景非常多，最经典的莫过于堆排序了, 堆排序是一种原地的、时间复杂度为 O(nlog n) 的排序算法，另外，堆也很适合用来做优先队列。

 

堆和树的结构其实是相似的, 堆有二叉堆, d-ary 堆, 2-3 堆, 斐波那契堆等等, 堆有一个特点就是每个父节点都大于等于它的儿子节点, 这种是大顶堆, 或者每个父节点都小于等于它的儿子节点, 这种是小顶堆，另外堆的儿子不分左右, 其中 java 中的 PriorityQueue 就是用二叉小顶堆实现的。

 

 

 

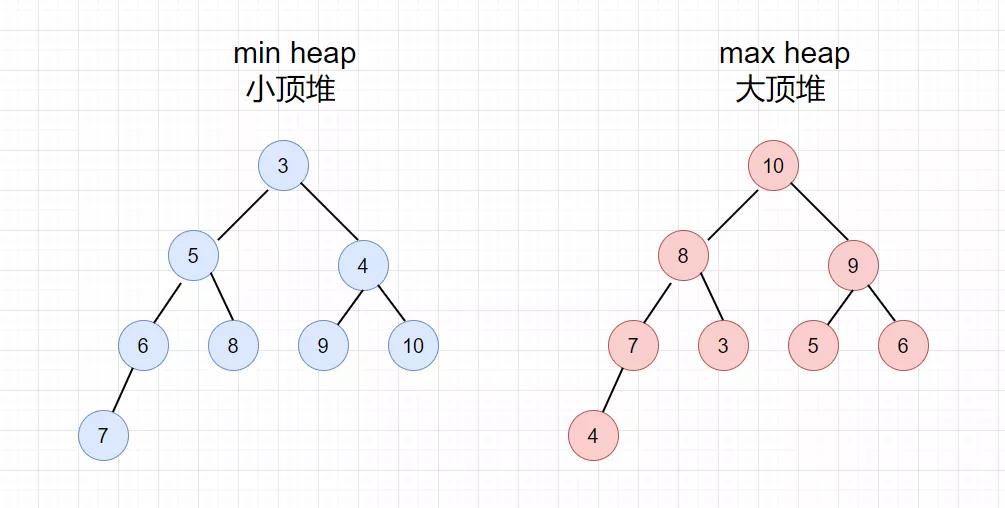
上面就是二叉堆, 而 .NET 6 中的 PriorityQueue 是由 d-ary 堆实现的, 而 d 表示父节点有几个儿子节点, .NET 6 中指定这个值为4，并且是小顶堆，也就是 “四叉小顶堆"。

 

 

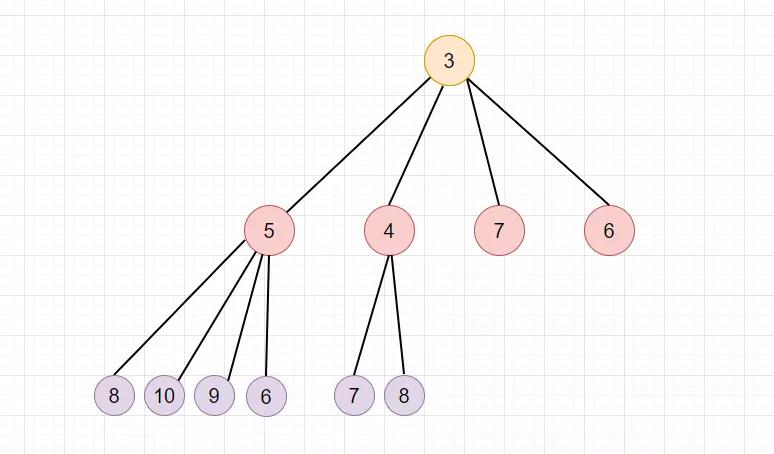
 那么如何在代码中实现呢？其实可以用数组存储堆, 我们可以通过”广度优先遍历“ 的方法, 把堆的节点映射到一个数组中，如下

 

 

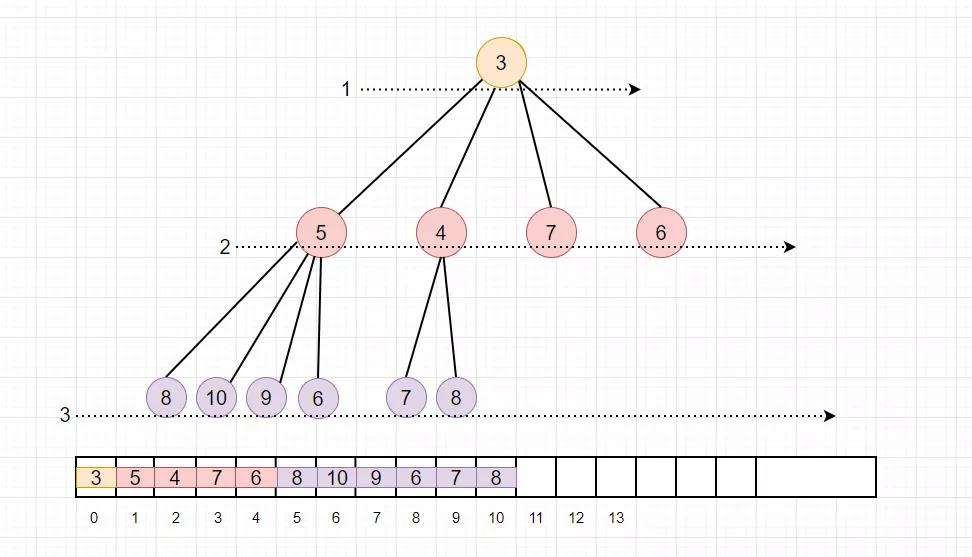
另外，堆和数组之间还有下面的关系

 

1.堆的顶点就是数组的第一个元素，也是最小的元素。
2.通过子节点的下标，就可以通过公式计算出父节点的下标, 公式为
P = (C - 1) / 4
其中 P = 父节点的下标, C = 子节点的下标

 

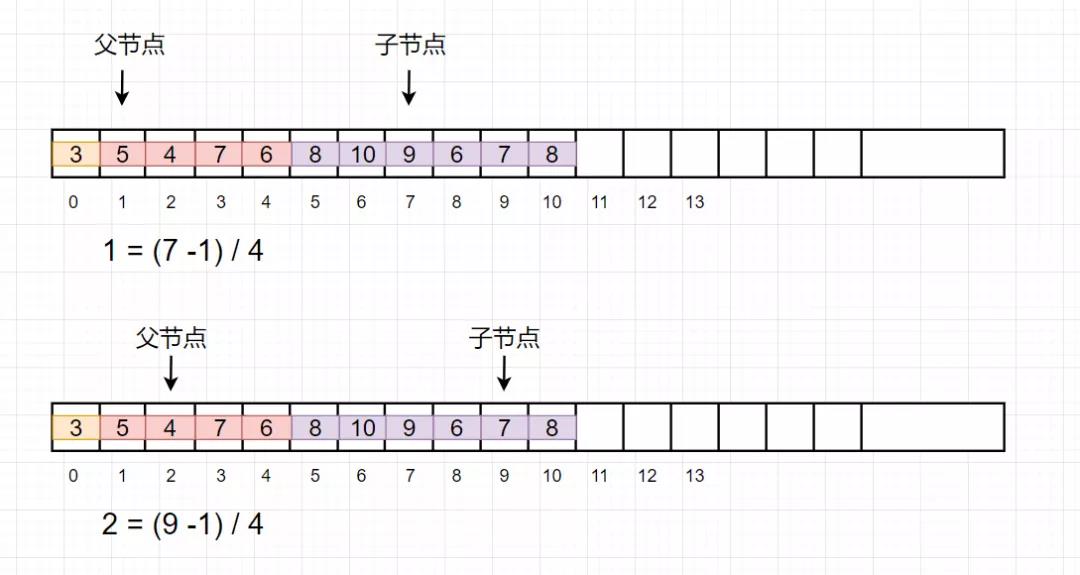
 现在优先队列的数据结构确定了, 接下来看元素的入队和出队。

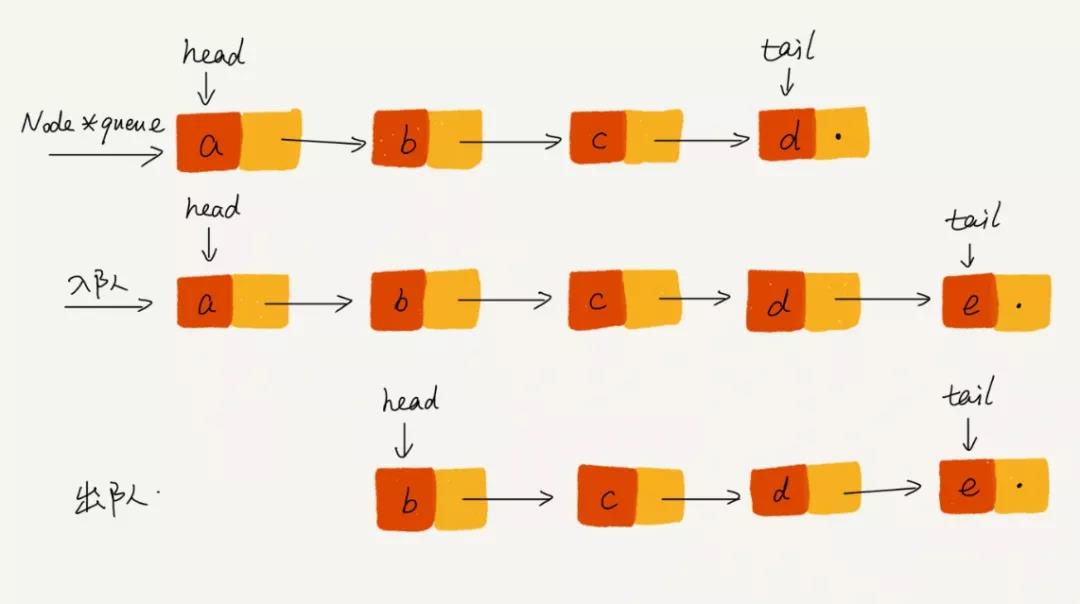
入队 Enqueue

使用堆来实现优先队列，入队操作2步完成, 非常简单！

 

1.添加新节点到末尾
2.通过上面的公式 P = (C - 1) / 4, 新的子节点和父节点进行大小对比，如果子节点比较小，那么就和父节点交换，重复这个过程，直到子节点大于或等于父节点，或者子节点变成堆顶，堆化完成, 这个交换过程是从下往上的, 入队的时间复杂度是 O(log n)。

 

 

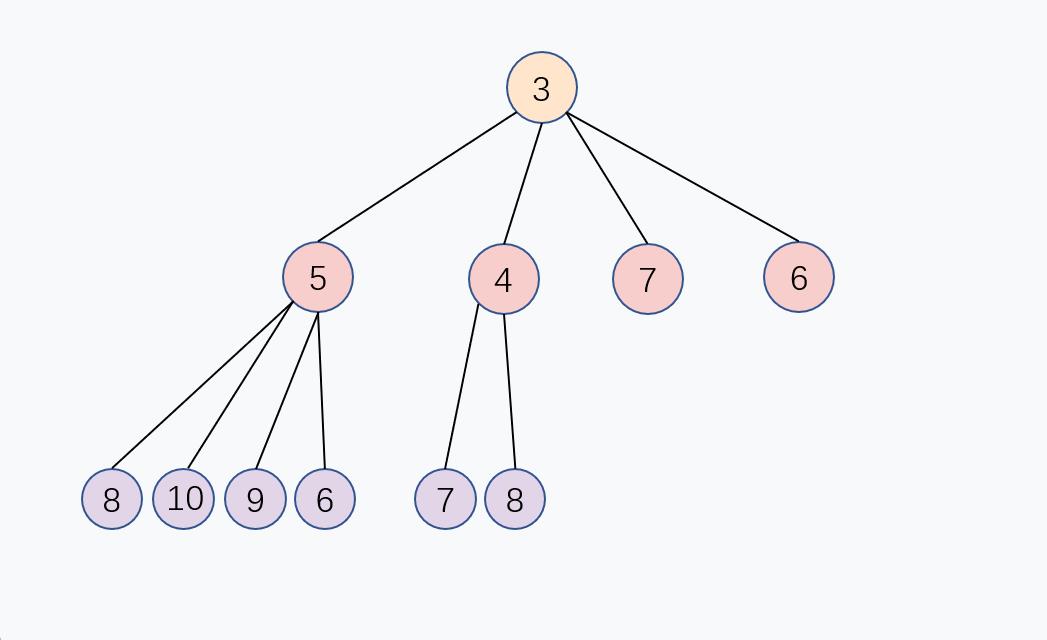
 出队 Dequeue

出队，就是每次取队列内最小的元素，基小顶堆结构，其实只需要取堆顶的元素即可，对应数组的第1个元素 array[0]。

你会发现，当取出堆顶元素以后，小顶堆的顶已经空了, 为了保持堆的结构，我们需要重新堆化。

和上面的入队 Enqueue 的逻辑有异曲同工之妙, 我们可以取堆的最后一个元素，把它放到堆顶, 然后父节点去和4个儿子节点比大小，如果比儿子节点大，就交换， 重复这个过程，直到父节点比4个儿子节点都大,

或者到达堆的最后一层，堆化完成，这个交换过程是从上往下的,出队的时间复杂度同样是 O(log n)。

另外，如果多个儿子节点都比父节点小，那父节点和最小的子节点交换。

 

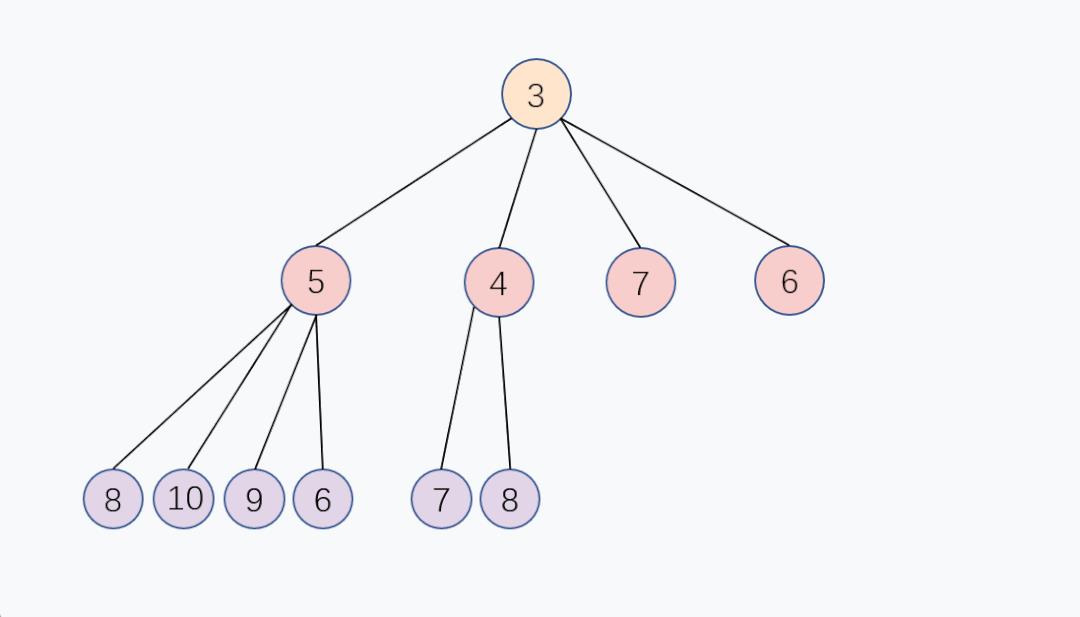
 扩容和收缩机制

 

优先队列是用数组实现的四叉小顶堆, 那么就存在数组的扩容和收缩的情况

 

扩容：最小为4，数组满的时候会扩大为当前容量的2倍。

 

收缩：数组不会自动收缩，不过可以手动调用 TrimExcess() 方法, 当空余的空间大于10% 的时候, 数组的长度会收缩到当前队列元素的数量。