力扣236单周赛题目分享

Posted 2023-05-01

参考技术A 共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按 顺时针顺序 从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1. 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：

从第 1 名小伙伴所在位置 开始 。
沿着顺时针方向数 k 名小伙伴，计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

示例 1：

输入：n = 5, k = 2

输出：3

解释：
游戏运行步骤如下：

示例 2：

输入：n = 6, k = 5

输出：1

解释：
小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

这是一道标准的约瑟夫环问题，类似的题目很多，比如剑指offer中有一道小朋友们的游戏与此题就如出一辙。大家找个链表画下题目就迎刃而解了，类似斐波那契数列一样，了解公式直接解题。

给你一个长度为. n. 的. 3 跑道道路. ，它总共包含. n + 1. 个. 点. ，编号为. 0. 到. n. 。一只青蛙从. 0. 号点第二条跑道. 出发. ，它想要跳到点. n. 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1. 的数组. obstacles. ，其中. obstacles[i]. （取值范围从 0 到 3）表示在点 i. 处的. obstacles[i]. 跑道上有一个障碍。如果. obstacles[i] == 0. ，那么点. i. 处没有障碍。任何一个点的三条跑道中. 最多有一个. 障碍。

比方说，如果. obstacles[2] == 1. ，那么说明在点 2 处跑道 1 有障碍。
这只青蛙从点 i. 跳到点 i + 1. 且跑道不变的前提是点 i + 1. 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在. 同一个. 点处. 侧跳. 到 另外一条. 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。
这只青蛙从点 0 处跑道 2. 出发，并想到达点 n. 处的 任一跑道 ，请你返回 最少侧跳次数. 。

注意：点 0. 处和点 n. 处的任一跑道都不会有障碍。

示例 1：

输入：obstacles = [0,1,2,3,0]

输出：2

解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。

注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例 2：

输入：obstacles = [0,1,1,3,3,0]

输出：0

解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：

输入：obstacles = [0,2,1,0,3,0]

输出：2

解释：最优方案如上图所示。总共有 2 次侧跳。

我的个人博客： https://qingfengpython.cn

力扣解题合集： https://github.com/BreezePython/AlgorithmMarkdown

力扣264周赛题解

题目

5906. 句子中的有效单词数

本题的解决思路就是去遍历该string，同时将判断条件在模拟的过程中进行判断即可，判断条件如下；

1.仅由小写字母、连字符和/或标点（不含数字）。

2.至多一个 连字符 '-' 。如果存在，连字符两侧应当都存在小写字母（"a-b" 是一个有效单词，但 "-ab" 和 "ab-" 不是有效单词）。

3.至多一个 标点符号。如果存在，标点符号应当位于 token 的 末尾 。

解决代码

class Solution { public:      int countValidWords(string s) {          int n = s.size(), res = 0;          for (int i = 0; i < n; i ++){             if (isalpha(s[i]) || s[i] == '.'  || s[i] == '!' || s[i] == ',') {                 int num = 0;                 while(i < n &&  s[i] != ' '){                     if (s[i] == '-'  && i < n-1 && isalpha(s[i + 1])) num ++;                     else if((s[i] == '-'  && i < n-1 && !isalpha(s[i + 1])) || ((s[i] == '.' || s[i]  == '!' || s[i] == ',') && (i < n-1 && s[i + 1] != ' ')) ||  isdigit(s[i])) num = 2;                     i ++;                 }                 i --;                 if (num <= 1) res ++;             }             else if(s[i] != ' '){                 while(i < n &&  s[i] != ' ') i ++;                 i --;             }          }          return res;      } };

5907.下一个更大的数值平衡数

读完该题，首先应该注意到该题的数据范围在n <= 1e6; 有了这个条件就可以考虑去枚举所有在n + 1  -  1e7这个范围内满足条件的最小值；该题的题目要求满足条件的值单个位置存在的数字个数等于该数字本身，并且严格大于给出的n；

为什么是1e7呢?因为该题是要求严格大于n的，n能够取到1e6，所以操作时可以向上取到1e7，就一定会存在严格大于n的值。

解决代码

const int N = 10, M = 1e7; class Solution { public:      int snt[N];      int nextBeautifulNumber(int n) {          for (int i = n + 1; i <= M; i ++){             memset(snt, 0, sizeof snt);             int k = i;             while(k > 0) {                 snt[k % 10] ++;                 k /= 10;             }             bool flag = false;             for (int j = 0; j <= 9; j ++){                 if (snt[j] > 0 &&  j != snt[j]) {                     flag = true;                     break;                 }             }             if (!flag) return i;          }          return -1;      } };

5908. 统计最高分的节点数目

该题题意：给出的是一个二叉树，想要得到的是删除某个节点的分支，所产生的新的分支的乘积的最大值的个数；所以此题可以采用dfs+回溯来解决该问题，在回溯的过程中返回分支所产生的节点，然后求其乘积，得到最大值，同时并记录其个数。解释如下：

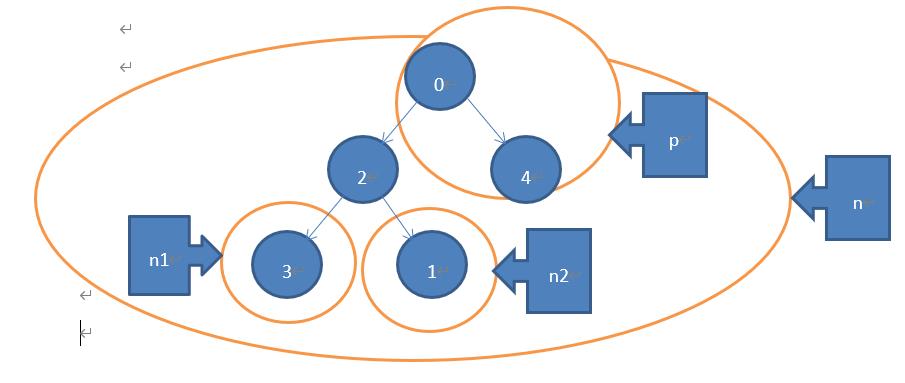
对于此案例，若是采用dfs+回溯的方法对于节点2来看；在回溯的过程中2节点的两个子节点3 ，1分别回溯到节点2的节点个数为n1，n2，但对于节点2而言还得计算其父节点部分所产生的个数为p， 整个二叉树的节点个数为n；已知子节点的回溯值n1, n2,如何求出父节点p的值呢？由上图可知：

p  =  n –  n1 – n2

有了此公式对于该问题也就很好解决了。

解决代码

class Solution { public:      int root, n, res;      unordered_map<int, vector<int>> mp;      typedef long long LL;      LL kk;      int dfs(int p){          LL maxv = 1;          int nums = 1;          for (int v: mp[p]) {             int k = dfs(v);             maxv = (LL)maxv * k;             nums += k;          }          if(p != root) maxv = (LL)maxv * (n-nums);          if (maxv > kk) {             res = 1;             kk = maxv;          }          else if (maxv == kk) {             res ++;          }          return nums;      }      int countHighestScoreNodes(vector<int>& ps) {          n = ps.size();          for (int i = 0; i < n; i ++){              if (ps[i] == -1) root = i;             else {                 mp[ps[i]].push_back(i);             }          }          dfs(root);          return res;      } };

5909. 并行课程 III

该题的题意：完成某一个课程前，必须先完成在它之前的先修课，那么此题就完全符合拓扑结构，故此可以采用拓扑图去解决该问题。如果要进行该点操作，必须首先完成其所有入度点的操作，因为完成每一个该点入度的时间不一样，所以我们取时间最晚的入度为执行该点的起始执行时间(因为最晚的入度时间点必定其他入度已经全部执行完成)；写出拓扑图+数组记录每一个点的起始时间就可解决该问题。

 解决代码

const int N = 50010; class Solution { public:      int n, r[N], dist[N];      vector<int> rlx[N];      void topu(vector<int> time){          queue<int> qu;          int n = time.size();          for (int i = 1; i <= n; i ++){             if (r[i] == 0) {                 qu.push(i);                 dist[i] = time[i-1];             }          }          while(qu.size()){             int v = qu.front();             qu.pop();             for (int x: rlx[v]){                 r[x] --;                 dist[x] = max(dist[x],  dist[v] + time[x-1]);                 if (r[x] == 0) qu.push(x);             }          }      }      int minimumTime(int n, vector<vector<int>>& rx,  vector<int>& time) {          n = time.size();          for (int i = 0; i < rx.size(); i ++){             int a = rx[i][0], b = rx[i][1];             r[b] ++;             rlx[a].push_back(b);          }          topu(time);          int res = 0;          for (int i = 1; i <= n; i ++) res = max(res, dist[i]);          return res;      } };

总结

本博客是力扣264场周赛的题解，如果存在不懂的地方可以在评论区提出，这里会耐心解答！关注公众号：算法与编程之美，我们会不断的更新力扣周赛题解，codeforces题解等比赛题解。

实习编辑：衡辉

稿件来源：深度学习与文旅应用实验室（DLETA）