LeetCode 第 58 场力扣夜喵双周赛（动态规划马拉车算法，前后缀处理）/ 第 253 场力扣周赛（贪心，LIS）
Posted Zephyr丶J
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了LeetCode 第 58 场力扣夜喵双周赛（动态规划马拉车算法，前后缀处理）/ 第 253 场力扣周赛（贪心，LIS）相关的知识，希望对你有一定的参考价值。
第 58 场力扣夜喵双周赛
两道600多
5193. 删除字符使字符串变好
题目描述
一个字符串如果没有 三个连续 相同字符，那么它就是一个 好字符串 。
给你一个字符串 s ，请你从 s 删除 最少 的字符，使它变成一个 好字符串 。
请你返回删除后的字符串。题目数据保证答案总是 唯一的 。
示例 1：
输入：s = “leeetcode”
输出：“leetcode”
解释：
从第一组 ‘e’ 里面删除一个 ‘e’ ，得到 “leetcode” 。
没有连续三个相同字符，所以返回 “leetcode” 。
示例 2：
输入：s = “aaabaaaa”
输出：“aabaa”
解释：
从第一组 ‘a’ 里面删除一个 ‘a’ ，得到 “aabaaaa” 。
从第二组 ‘a’ 里面删除两个 ‘a’ ，得到 “aabaa” 。
没有连续三个相同字符，所以返回 “aabaa” 。
示例 3：
输入：s = “aab”
输出：“aab”
解释：没有连续三个相同字符，所以返回 “aab” 。
提示：
1 <= s.length <= 105
s 只包含小写英文字母。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/delete-characters-to-make-fancy-string
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
四分钟写出来的，还行吧
class Solution {
public String makeFancyString(String s) {
int l = s.length();
StringBuffer sb = new StringBuffer();
for(int i = 0; i < l; i++){
char temp = s.charAt(i);
if(i > 1 && temp == s.charAt(i - 1) && temp == s.charAt(i - 2)){
continue;
}
sb.append(temp);
}
return sb.toString();
}
}
5827. 检查操作是否合法
题目描述
给你一个下标从 0 开始的 8 x 8 网格 board ，其中 board[r][c] 表示游戏棋盘上的格子 (r, c) 。棋盘上空格用 ‘.’ 表示，白色格子用 ‘W’ 表示，黑色格子用 ‘B’ 表示。
游戏中每次操作步骤为：选择一个空格子，将它变成你正在执行的颜色（要么白色，要么黑色）。但是，合法 操作必须满足：涂色后这个格子是 好线段的一个端点 （好线段可以是水平的，竖直的或者是对角线）。
好线段 指的是一个包含 三个或者更多格子（包含端点格子）的线段，线段两个端点格子为 同一种颜色 ，且中间剩余格子的颜色都为 另一种颜色 （线段上不能有任何空格子）。你可以在下图找到好线段的例子：
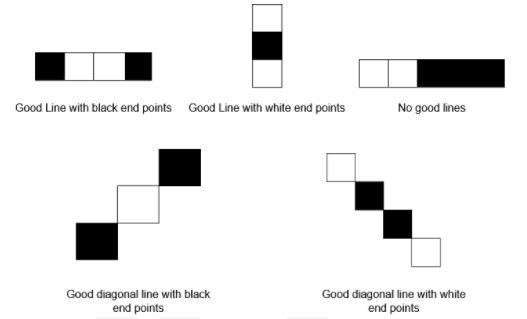
给你两个整数 rMove 和 cMove 以及一个字符 color ，表示你正在执行操作的颜色（白或者黑），如果将格子 (rMove, cMove) 变成颜色 color 后，是一个 合法 操作，那么返回 true ，如果不是合法操作返回 false 。
示例 1：
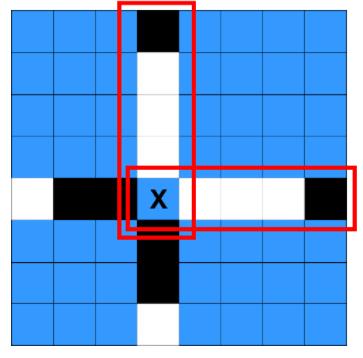
输入：board = [[".",".",".",“B”,".",".",".","."],[".",".",".",“W”,".",".",".","."],[".",".",".",“W”,".",".",".","."],[".",".",".",“W”,".",".",".","."],[“W”,“B”,“B”,".",“W”,“W”,“W”,“B”],[".",".",".",“B”,".",".",".","."],[".",".",".",“B”,".",".",".","."],[".",".",".",“W”,".",".",".","."]], rMove = 4, cMove = 3, color = “B”
输出：true
解释：’.’，‘W’ 和 ‘B’ 分别用颜色蓝色，白色和黑色表示。格子 (rMove, cMove) 用 ‘X’ 标记。
以选中格子为端点的两个好线段在上图中用红色矩形标注出来了。
示例 2：
输入：board = [[".",".",".",".",".",".",".","."],[".",“B”,".",".",“W”,".",".","."],[".",".",“W”,".",".",".",".","."],[".",".",".",“W”,“B”,".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",“B”,“W”,".","."],[".",".",".",".",".",".",“W”,"."],[".",".",".",".",".",".",".",“B”]], rMove = 4, cMove = 4, color = “W”
输出：false
解释：虽然选中格子涂色后，棋盘上产生了好线段，但选中格子是作为中间格子，没有产生以选中格子为端点的好线段。
提示：
board.length == board[r].length == 8
0 <= rMove, cMove < 8
board[rMove][cMove] == ‘.’
color 要么是 ‘B’ 要么是 ‘W’ 。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/check-if-move-is-legal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
我当时没多想，就是上下左右以及四个角方向，复制了八份代码写的：
每个方向，如果碰到了空白，就不可能有好线段；如果第二个就碰到了相同的颜色，也不可能；如果能走到后面且后面有相同的颜色，就返回true
class Solution {
public boolean checkMove(char[][] board, int rMove, int cMove, char color) {
//意思是从这个点变色以后，有以这个点为端点的号线段
int m = board.length;
if(m == 0)
return false;
int n = board[0].length;
if(n == 0)
return false;
//左
for(int i = cMove - 1; i >= 0; i--){
if(!inarea(rMove, i, m, n))
break;
if(board[rMove][i] == '.')
break;
if(board[rMove][i] == color && cMove - i > 1){
return true;
}
if(board[rMove][i] == color)
break;
}
//右
for(int i = cMove + 1; i < n; i++){
if(!inarea(rMove, i, m, n))
break;
if(board[rMove][i] == '.')
break;
if(board[rMove][i] == color && i - cMove > 1){
return true;
}
if(board[rMove][i] == color)
break;
}
//上
for(int i = rMove - 1; i >= 0; i--){
if(!inarea(i, rMove, m, n))
break;
if(board[i][cMove] == '.')
break;
if(board[i][cMove] == color && rMove - i > 1){
return true;
}
if(board[i][cMove] == color)
break;
}
//下
for(int i = rMove + 1; i < m; i++){
if(!inarea(i, rMove, m, n))
break;
if(board[i][cMove] == '.')
break;
if(board[i][cMove] == color && i - rMove > 1){
return true;
}
if(board[i][cMove] == color)
break;
}
//左上
for(int i = 1; i < Math.max(m, n); i++){
int row = rMove - i;
int col = cMove - i;
if(!inarea(row, col, m, n))
break;
if(board[row][col] == '.')
break;
if(board[row][col] == color && i > 1){
return true;
}
if(board[row][col] == color)
break;
}
//左下
for(int i = 1; i < Math.max(m, n); i++){
int row = rMove + i;
int col = cMove - i;
if(!inarea(row, col, m, n))
break;
if(board[row][col] == '.')
break;
if(board[row][col] == color && i > 1){
return true;
}
if(board[row][col] == color)
break;
}
//右下
for(int i = 1; i < Math.max(m, n); i++){
int row = rMove + i;
int col = cMove + i;
if(!inarea(row, col, m, n))
break;
if(board[row][col] == '.')
break;
if(board[row][col] == color && i > 1){
return true;
}
if(board[row][col] == color)
break;
}
//右上
for(int i = 1; i < Math.max(m, n); i++){
int row = rMove - i;
int col = cMove + i;
if(!inarea(row, col, m, n))
break;
if(board[row][col] == '.')
break;
if(board[row][col] == color && i > 1){
return true;
}
if(board[row][col] == color)
break;
}
return false;
}
public boolean inarea(int x, int y, int m, int n){
return x >= 0 && x < m && y >= 0 && y < n;
}
}
5828. K 次调整数组大小浪费的最小总空间
题目描述
你正在设计一个动态数组。给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是 i 时刻数组中的元素数目。除此以外，你还有一个整数 k ，表示你可以 调整 数组大小的 最多 次数（每次都可以调整成 任意 大小）。
t 时刻数组的大小 sizet 必须大于等于 nums[t] ，因为数组需要有足够的空间容纳所有元素。t 时刻 浪费的空间 为 sizet - nums[t] ，总 浪费空间为满足 0 <= t < nums.length 的每一个时刻 t 浪费的空间 之和 。
在调整数组大小不超过 k 次的前提下，请你返回 最小总浪费空间 。
注意：数组最开始时可以为 任意大小 ，且 不计入 调整大小的操作次数。
示例 1：
输入：nums = [10,20], k = 0
输出：10
解释：size = [20,20].
我们可以让数组初始大小为 20 。
总浪费空间为 (20 - 10) + (20 - 20) = 10 。
示例 2：
输入：nums = [10,20,30], k = 1
输出：10
解释：size = [20,20,30].
我们可以让数组初始大小为 20 ，然后时刻 2 调整大小为 30 。
总浪费空间为 (20 - 10) + (20 - 20) + (30 - 30) = 10 。
示例 3：
输入：nums = [10,20,15,30,20], k = 2
输出：15
解释：size = [10,20,20,30,30].
我们可以让数组初始大小为 10 ，时刻 1 调整大小为 20 ，时刻 3 调整大小为 30 。
总浪费空间为 (10 - 10) + (20 - 20) + (20 - 15) + (30 - 30) + (30 - 20) = 15 。
提示：
1 <= nums.length <= 200
1 <= nums[i] <= 106
0 <= k <= nums.length - 1
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-total-space-wasted-with-k-resizing-operations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
隐约感受到了动态规划的力量，其实状态都想好了，但是还是没规出来，动态规划要好好再练一次了！
实际上就是在区间里选k个位置，然后保证被分成的k+1个区间每个区间数组的大小 sizet都是各自的最大值，这个也想到了
dp[i][j]表示到第i个位置，总共分成j段的浪费最小值，具体看注释
改了半天终于对了
也可以从前往后递推，即枚举第j + 1个位置
class Solution {
public int minSpaceWastedKResizing(int[] nums, int k) {
//做一下
int l = nums.length;
//首先预处理每一段的最大值，和如果赋予这一段这个最大值，浪费空间是多少
int[][] lost = new int[l][l];
for(int i = 0; i < l; i++){
int max = 0;
int pre = 0;
for(int j = i; j < l; j++){
pre = pre + nums[j];
max = Math.max(max, nums[j]);
lost[i][j] = max * (j - i + 1) - pre;
//System.out.print(lost[i][j] + " ");
}
//System.out.println();
}
//dp[i][j]表示到第i个位置，总共分成了j段浪费的最小值
//调整了k次会分成k+1段
int[][] dp = new int[l + 1][k + 2];
//初始化，赋最大值
//0位置分成0份，为0
for(int i = 1; i <= l; i++){
Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
}
//怎么转移呢，这个不会
//枚举最后一段的长度，这个是怎么想到的呢
//我记得当时做题的时候，我想的是从dp[i - 1][j] 和 dp[i][j- 1]转移的，然后不知道该怎么转移
//如果从dp[i - 1][j - 1]转移的话，就表示之前i - 1位置分成j - 1段，如果要多分一段，就枚举这一段的长度
//得到dp[i][j]
for(int i = 1; i <= l; i++){
for(int j = 1; j <= k + 1; j++){
//枚举i - 1这一段的长度，也就是这一段可以从0开始到i
//相当于把之前t的长度分成了j - 1 份，然后把剩下的t 到 i- 1 分成了一份
for(int t = 1; t <= i; t++){
dp[i][j] = Math.min(dp[i][j], dp[t - 1][j - 1] + lost[t - 1][i - 1]);
}
}
}
return dp[l][k + 1];
}
}
5220. 两个回文子字符串长度的最大乘积
题目描述
给你一个下标从 0 开始的字符串 s ，你需要找到两个 不重叠的回文 子字符串，它们的长度都必须为 奇数 ，使得它们长度的乘积最大。
更正式地，你想要选择四个整数 i ，j ，k ，l ，使得 0 <= i <= j < k <= l < s.length ，且子字符串 s[i…j] 和 s[k…l] 都是回文串且长度为奇数。s[i…j] 表示下标从 i 到 j 且 包含 两端下标的子字符串。
请你返回两个不重叠回文子字符串长度的 最大 乘积。
回文字符串 指的是一个从前往后读和从后往前读一模一样的字符串。子字符串 指的是一个字符串中一段连续字符。
示例 1：
输入：s = “ababbb”
输出：9
解释：子字符串 “aba” 和 “bbb” 为奇数长度的回文串。乘积为 3 * 3 = 9 。
示例 2：
输入：s = “zaaaxbbby”
输出：9
解释：子字符串 “aaa” 和 “bbb” 为奇数长度的回文串。乘积为 3 * 3 = 9 。
提示：
2 <= s.length <= 10^5
s 只包含小写英文字母。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-product-of-the-length-of-two-palindromic-substrings
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
看到数据范围，就知道肯定得马拉车，然后忘的一干二净了
首先再学习马拉车算法，看之前做的最长回文子串中自己写的理解
其实想通了也很好写，主要就是充分利用回文的特性
下面为LeetCode5.最长回文子串中写的马拉车算法：
class Solution {
//在我心里，weiwei哥基本就是那个男人，tmd太详细了，想看不懂都难啊
//这个Manacher算法，看了官解，一脸懵逼，不知道在说什么，
//这里总结一下它的主要思想，就是构造一个新的字符串，新字符串在原字符串每一个字符之间加了一个新的符号，左右也要加
//使得整个字符串的长度边为2*len+1
//然后也是中心扩散的思想，用一个数组记录所有中心最长的扩散距离p[]
//这个计算出来的最大的p[i]就是最长回文串的长度
//然后呢，如何降低复杂度，这就是难理解的地方了
//用一个maxRight和一个center分别记录当前能扩散到的最右边的地方和对应的中心
//从左到右填p[]，当i>=maxRight的时候，就用中心扩散的方法进行填表
//当i<maxRight的时候，i关于center的中心位置mirror，还有maxRight关于center的中心位置这几个点决定了如何更新p[]
//当maxRight - i > p[mirror]的时候，因为关于center是中心对称的，因此p[i]=p[mirror]
//当maxRight - i = p[mirror]的时候，此时因为maxRight以后 左边没有相应的参照点了，因此还需要用中心扩散继续扩大maxRight
//当maxRight - i < p[mirror]的时候，此时p[i]在扩展到maxRight，到这里，是对称的，
//maxRight以后，如果还能继续扩展，那么p[i]的左端，center的右端肯定有一个与之对称，在镜像过去，肯定等于maxLeft左边的值，
//那么，这个maxRight就不对了，因此不可以继续扩展（也能从左到右思考，找出矛盾）
//这样就可以完整的把表填好了
public String longestPalindrome(String s) {
// 特判
int len = s.length();
if (len < 2) {
return s;
}
// 得到预处理字符串
String str = addBoundaries(s, '#');
// 新字符串的长度
int sLen = 2 * len + 1;
// 数组 p 记录了扫描过的回文子串的信息
int[] p = new int[sLen];
// 双指针，它们是一一对应的，须同时更新
int maxRight = 0; //对应目前遍历过的回文串最右边的下标
int center = 0; //对应的中心位置
// 当前遍历的中心最大扩散步数，其值等于原始字符串的最长回文子串的长度
int maxLen = 1;
// 原始字符串的最长回文子串的起始位置，与 maxLen 必须同时更新
int start = 0;
for (int i = 0; i < sLen; i++) {
//如果当前位置下标在maxRight内，那么可以根据回文串的性质减少计算
if (i < maxRight) {
//首先计算i关于中心对称的下标mirror
int mirror = 2 * center - i;
// 这一行代码是 Manacher 算法的关键所在，要结合图形来理解
// 如果maxRight - i > p[mirror]，那么说明扩散不到maxRight外，因此直接p[i] = p[mirror]
//如果等于，那么就先取p[mirror]的值，然后再中心扩散
//如果小于，首先肯定能取到maxRight - i，如果还能往后继续扩散的话，会和左边相同，从而使maxRight的长度增加，所以肯定不能扩散了，所以取maxRight - i
//总结，取两者的最小值
p[i] = Math.min(maxRight - i, p[mirror]);
}
// 下一次尝试扩散的左右起点，能扩散的步数直接加到 p[i] 中
//取到当前p[i]以后，中心扩散，如果还能扩散就继续
int left = i - (1 + p[i]);
int right = i + (1 + p[i]);
// left >= 0 && right < sLen 保证不越界
// str.charAt(left) == str.charAt(right) 以上是关于LeetCode 第 58 场力扣夜喵双周赛（动态规划马拉车算法，前后缀处理）/ 第 253 场力扣周赛（贪心，LIS）的主要内容，如果未能解决你的问题，请参考以下文章
LeetCode 第 59 场力扣夜喵双周赛（最短路径数+迪杰斯特拉动态规划+最长公共前缀问题） / 第255场周赛（二进制转换，分组背包，子集还原数组（脑筋急转弯））
LeetCode494. 目标和 / 474. 一和零 / 203. 移除链表元素 / 第 244 场力扣周赛
第 256 场力扣周赛（状态压缩+dp，二进制子序列的动规940）