大数据的统计学基础——事件概率

Posted 2020-11-01 liumuz

总体均值：μ=Σx / N；                 样本均值：=Σx / n；

总体方差：；        样本方差：

 

 四分位数的选择：

选择分位数的百分比值为y，样本总量为n，则分位数的计算可由以下的式子计算：

若L是一个整数，则取L和L+1的的平均值；

若L不是一个整数，则取下一个最近的整数。

如：求1，2，3，4，5的四分位数。

则有L₂₅ = 5*（25/100）=1.25，则四分位数为2；

随机试验的特点：

1、可以在相同的情况下重复进行；

2、试验的可能结果不止一个，但试验前知道所有的实验结果；

3、试验前不确定哪个结果会发生；

对于随机试验E，其所有可能出现的结果的集合称为样本空间，记为S，S中的每个元素，即E的每个可能结果，称为样本点。

一般的，我们称为样本空间S中的某个子集为随机试验E的随机事件，简称事件。由一个样本点组成的单点集，称为基本事件。

必然事件：在每个试验中一定会发生的事件；

不可能事件：在每个试验中一定不会发生的事件。

事件关系：

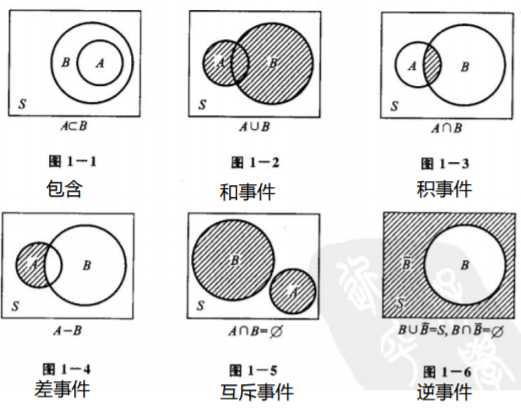
事件运算定律:

交换律：A∩B = B∩A；A∪B = B∪A；

结合律:A∩B∩C = A∩（B∩C）； A∪B∪C = A∪（B∪C）；

分配律：A∪（B∩C）= （A∪B）∩（A∩C）；

德摩根律：；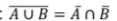

在相同情况下，重复n次试验，事件A发生的次数n_A称为A发生的频数；n_A/n称为事件A发生的频率；

大量的试验证明，当试验的重复次数n逐渐增大时，事件A发生的频率会逐渐稳定于某个常数p，p称为事件A发生的概率。记事件A发生的概率为p（A）；

概率需要满足以下的条件：

1、非负性。P(A)>=0;

2、规范性。对于必然事件A有P（A） = 1；

3、可列可加性。对于两两互不相容的事件A₁，A₂，A₃...,即A_i*A_j =，i≠j，i，j= 1，2，3，4....，有P（A₁∪A₂∪A₃∪A₄...)=P（A₁）+P（A₂）+P（A₃）+P（A₄）+...

概率的性质:

 1、P（）=0.不可能事件的概率为0；   

2、有限可加性：对于两两互不相容的事件A₁，A₂，A₃...An，即A_i*A_j =，i≠j，i，j= 1，2，3，4....，有P（A₁∪A₂∪A₃∪A₄...∪An)=P（A₁）+P（A₂）+P（A₃）+P（A₄）+...P（An）；

3、对于事件A，B，若有B包含于A，则有P（A-B）=P（A）-P（B）；

4、对于任一事件A，P（A）<1;

5、对于任一事件A，有；

6、对于A、B两个事件，有P（A∪B)=P（A）+P（B）-P（A∩B）；

古典概型：

对于试验E，若满足：

1、试验的样本空间只包含有限个元素；

2、试验中每个基本元素发生的可能性相同，即每个基本事件发生的概率相等；

我们称这样的事件为古典概型，也称为等可能概型；

设古典概型的样本空间为S={e₁，e₂，e₃....e_n},根据古典概型的定义，有：P（e₁）=P（e₂）=...=P(e_n)，而基本事件是互斥的，所以有1=P（s）=P（e₁）+P（e₂）+...P（e_n）。P（e₁）=P（e₂）=P（e₃）=...=P(e_n)=1/n;

对于事件A，若A包含k个基本事件，则有P（A）=k/n；

排列组合：

排列：从n个元素中，任取m个元素，按照一定的顺序拍成一列，叫做从n个不同元素中取出m个元素的一个排列，与顺序有关；

组合：从n个元素中，任取m个元素，并成一组，叫做从n个元素中去除m个元素的一个组合，与顺序无关；

从n个不同的元素中取出m个元素，并按照一定的顺序进行排列，则一共有中排列方式；

从n个不同的元素中取出m个元素，则一共有:种排列方式。

设又N件产品，其中有D件次品，今从中任取n件，其中恰好有k（k≤D）件次品的概率为：

 

过程：N件产品中取出n件产品的取法有种（），在D件次品中选出k件次品的取法有种。在N-D件正品中取出n-k件正品的取法有种，由乘法原理知从n件产品中取出恰好有k件次品的概率为:

几何概型：

对于试验E， 若满足：

1、试验的样本包含无限个元素；

2、试验中每个基本事件发生的可能性相同，即每个基本事件发生的概率相等；

这样的事件称为几何概型；

P（A）=构成事件A的区域长度（面积或体积）/ 试验的全部结果所构成的区域长度（面积或体积）；