机器学习基础统计学(频率派与贝叶斯派)
Posted fanshaoxiang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习基础统计学(频率派与贝叶斯派)相关的知识,希望对你有一定的参考价值。
一、频率派
假设X为随机数据,其矩阵表示维度为N,假设θ为X随机数的特征,频率派认为在一次实验中,如果时间A发生了,那么则认为事件A的发生一定是事件A的概率最大,记为P(x=A)最大,由假设可知事件A发生的概率和θ有关。
极大似然是指一次试验就发生的事件,这个事件本身发生概率最大,极大似然估计具体求解与推导公式如下:
假设:x是服从某个概率的分别,可以用概率P =p(x|Θ),其中Θ为概率分布的某个特征值,p(x|Θ)为事件x发生的概率。现在进行一次关于x的试验,得到样本值为(x1,x2,x3,···,xn)时,依据极大似然估计原理可以得出;
L(Θ) = L(x1,x2,x3,···,xn;Θ)
= p(x1|Θ)·p(x2|Θ),···,p(xn|Θ)
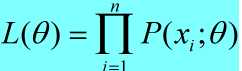
由极大使然估计原理可知:L(Θ)最大,则可以改写如下:

为了表示计算方便,等式双方取对数:
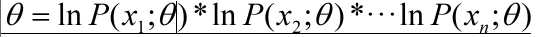
令对数释然函数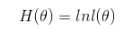
求解:
设 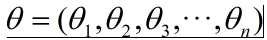
为了使Θ参数值最大,则方程可为:
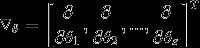
令其偏导数为0求偏微分解方程组,求解方程可以采用梯度下降法
梯度下降法原理如下:(这里采用例子进行说明)
假设求下列函数最小值 : 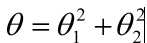
采用梯度下降法:我们假设初始点为为(1,1),学习率为0.1,对Θ求导,则Θ = 2Θ1+2Θ2
则函数的梯度为: 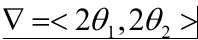
计算过程如下:

其数学原理可以参考如下博客链接:
https://blog.csdn.net/weixin_42278173/article/details/81511646
若可导:
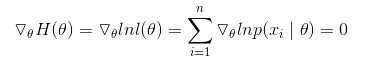
二、贝叶斯统计学
先了解相关概念“先验概率”与“后验概率”,以一个例子来说明:假设喜欢打球的人在人群中的占比为30%,即100人中会有30个人爱好球类。
则有: P(球) = 30%,这个就叫作"先验概率"。
设:现在从爱好球类的人中,已知50%的人喜欢喝可乐。也就是说,如果从爱好球类的人抽样,该检测法有50%的概率会喜欢和可乐,但也有50%的概率不爱喝可乐。
用概率条件概率表示即为:P(爱喝可乐|喜爱球类)=50%
现在我们想知道的是:在随机抽样一个人,某人的爱喝可乐P(爱喝可乐|人群中),这个称为"后验概率"。
“贝叶斯公式”其实就是已知先验概率求解后验概率,具体公式推导如下:
基础公式1:
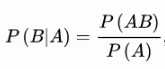
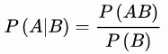
注:P(B|A)为在A条件下B发生的概率
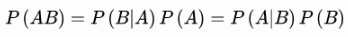
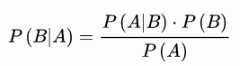
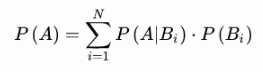
则全概率公式为: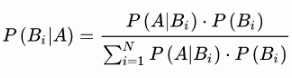
以上是关于机器学习基础统计学(频率派与贝叶斯派)的主要内容,如果未能解决你的问题,请参考以下文章