利用SPSS进行一致性检验并计算Kappa值
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了利用SPSS进行一致性检验并计算Kappa值相关的知识,希望对你有一定的参考价值。
参考技术A SPSS:一致性检验,如何计算Kappa值?研究问题为:探讨两位警察对受试者行为判断的一致性,受试者行为的判定结果为“正常”或“可疑”。采用Cohen's kappa系数分析。一、问题与数据
二、问题的分析
在本研究中,研究者拟探讨两位警察对受试者行为判断的一致性,我们推荐使用 Cohen's kappa系数分析。一般来说,采用Cohen's kappa系数的研究设计需要满足以下5项假设:
假设1:判定结果是分类变量且互斥。如本研究中受试者行为的判定结果为“正常”或“可疑”,属于分类变量,并且相互排斥。
假设2:要求进行观测变量配对,即不同观测者判定的对象相同。如本研究中,两位警察观看的是同一组录像,编号统一。
假设3:每个观察对象可能被判定的结果种类相同。如本研究中每位受试者的行为都可能被判定为“正常”或“可疑”。
假设4:观测者之间相互独立。这要求不同观测者独立完成结果判定,相互不干扰。
假设5:由固定的两位观测者完成所有判定。如本研究中由两位警察分别观看100段录像,中途不换人。
根据研究设计,我们认为本研究符合Cohen's kappa系数的5项假设,可以采用该分析方法进行一致性评价。
三、SPSS操作
1. 在主菜单点击Analyze→DescriptiveStatistics→Crosstabs
出现下图:
2. 分别将Officer1和Officer2变量放入Row(s)和Column(s)栏
3. 点击Statistics
4. 点选Kappa
5. 点击Continue→Cells
6. 点击Observed→Continue→OK
注释:如果大家想要得到频率的预测值,可以点击Counts栏中的Expected;若大家还想得到百分比值,可以点击Percentages栏中的Row、Column和Total
四、结果解释
1. 一般结果
在分析Cohen's kappa系数之前,我们有必要了解一下研究数据的基本情况,如下:
从上表可以看出,本研究共有100对有效数据(Valid栏),没有缺失(Missing栏),总数据为100例(Total栏)。Officer1和Officer2的交叉表,如下:
SPSS根据数据录入情况,分别输出Officer1和Officer2认为“正常”和“可疑”的数量。其中,左上和右下的数据是经Officer1和Officer2判断一致的,如下标黄的部分:
从上表可以看出,两位警察都认为其中85位受试者行为“正常”,7位受试者行为“可疑”,即这两位警察在92位受试者的行为上判断一致。从另一个角度来说,Officer1认为87位受试者行为“正常”,而Officer2认为91位受试者行为“正常”,如下标黄部分:
同理,这个表也输出了Officer1和Officer2判断不一致的数据,如下标黄部分:
从上表可知,在本研究中,两位警察对6+2=8为受试者的行为判断不一致。根据这些数据,我们可知Officer1和Officer2在对92÷100×100%=92%的受试者行为判断上一致。但是这种一致率没有考虑机遇因素的影响,我们还要依据Cohen's kappa系数具体分析。
2. Cohen's kappa系数
与直接计算的一致率不同的是,Cohen's kappa系数考虑了机遇一致率对结果的影响。具体来说,在本研究中即使两位警察并不依据专业经验,而是随意评价受试者的行为,他们也会在对一些判断上出现一致结果。但是,这些由于机遇因素导致的一致结果并不是我们想要的,会高估实际一致率。因此,我们需要在计算Cohen's kappa系数时,剔除机遇一致率,公式如下:
Value栏提示Cohen's kappa系数值,如下标黄部分:
从上表可知,本研究的Cohen's kappa=0.593。一般来说,Cohen's kappa系数分布在-1到1之间。若Cohen's kappa系数小于0,说明观察一致率小于机遇一致率,在实际研究中很少出现。若Cohen's kappa系数等于0,说明观察一致率等于机遇一致率,结果完全由机遇因素导致。若Cohen's kappa系数大于0,说明研究对象之间存在一定的一致性,Cohen's kappa系数越接近1,一致性越大。
那么,本研究中Cohen's kappa系数为0.593,说明一致性如何呢?Cohen's kappa系数值反映的一致性强度,如下:
从上表可知,本研究中Cohen's kappa系数0.593,说明具有中等强度一致性。但是,值得注意的是,我们并不能轻易地根据表1直接对比不同研究的Cohen's kappa系数。因为Cohen's kappa系数在计算过程中剔除了机遇一致率,也因此受到研究数据边际分布程度的影响。所以,我们只能比较具有相同边际分布数据的Cohen's kappa系数,而不能直接对比数据边际分布不同的研究。
此外,SPSS输出Symmetric Measures表格,提示Cohen's kappa系数的统计检验结果,如下标黄部分:
提示,本研究的Cohen's kappa系数与0的差异具有统计学意义(P<0.001)。同时,我们也可以根据该表格计算Cohen's kappa系数的95%置信区间,如下标黄部分:
可见,本研究中Cohen's kappa系数的标准误为0.129。鉴于本研究样本量较大,我们认为研究数据接近正态分布。从而计算Cohen's kappa系数的95%置信区间为0.593±1.96×0.129=0.593±0.253。即,本研究Cohen's kappa系数为0.593(95% CI为0.340 -0.846)。
五、撰写结论
本研究采用Cohen's kappa系数分析两位警察对100位受试者行为判断的一致性。结果显示,这两位警察都认为其中85位受试者行为“正常”,7位受试者行为“可疑”。但同时有6位受试者被警察1认定为“可疑”,而被警察2认定为“正常”;也有2位受试者被警察1认定为“正常”,而被警察2认定为“可疑”。
总的来说,这两位警察判断结果的Cohen's kappa系数为0.593(95% CI为0.340 -0.846),P<0.001,具有中等强度一致性。
kappa一致性系数和spearman系数的区别
kappa一致性系数和spearman系数的区别是:
(1)kappa一致性系数:
它是通过把所有地表真实分类中的像元总数(N)乘以混淆矩阵对角线(Xkk)的和,再减去某一类地表真实像元总数与被误分成该类像元总数之积对所有类别求和的结果,再除以总像元数的平方减去某一类中地表真实像元总数与该类中被误分成该类像元总数之积对所有类别求和的结果所得到的。
计算公式编辑
两幅栅格图的kappa计算公式为 k = (Po-Pc)/(1-Pc)
设栅格总象元数为n,真实栅格为1的象元数为a1,为0的象元数为a0,模拟栅格为1的象元数为b1,为0的象元数为b0,两个栅格对应象元值相等的象元数为s,则
Po = s/n, Pc = (a1*b1+a0*b0)/(n*n)
在arcmap里,a1、a0、b1、b0从属性表可读出,s用raster calculator配合con()函数不难求出。
kappa计算结果为-1~1,但通常kappa是落在 0~1 间,可分为五组来表示不同级别的一致性:0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)。
(2)spearman系数:
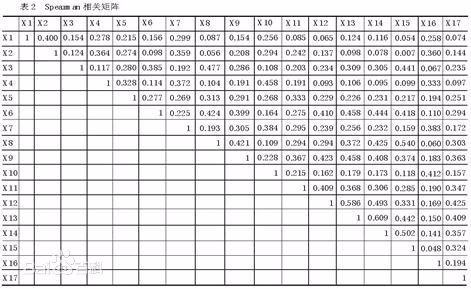
对不服从正态分布的资料、原始资料等级资料、一侧开口资料、总体分布类型未知的资料不符合使用积矩相关系数来描述关联性。此时可采用秩相关(rank correlation),也称等级相关,来描述两个变量之间的关联程度与方向。
计算步骤:
⑴编秩:将两变量X、Y成对的观察值分别从小到大顺序编秩,用pi表示xi的秩次;用qi表示yi的秩次。若观察值相同取平均秩次。
⑵将秩次带入公式计算:
⑶由样本算得的秩相关系数是否有统计学意义,应作假设检验。
检验编辑
⑴建立假设检验,确定检验水准:
⑵计算检验统计量:
查秩相关系数界值表,若超过界值表,则拒绝 ; 作 检验。
参考技术Akappa系数
它是通过把所有地表真实分类中的像元总数(N)乘以混淆矩阵对角线(Xkk)的和,再减去某一类地表真实像元总数与被误分成该类像元总数之积对所有类别求和的结果,再除以总像元数的平方减去某一类中地表真实像元总数与该类中被误分成该类像元总数之积对所有类别求和的结果所得到的。
计算公式编辑
两幅栅格图的kappa计算公式为 k = (Po-Pc)/(1-Pc)
设栅格总象元数为n,真实栅格为1的象元数为a1,为0的象元数为a0,模拟栅格为1的象元数为b1,为0的象元数为b0,两个栅格对应象元值相等的象元数为s,则
Po = s/n, Pc = (a1*b1+a0*b0)/(n*n)
在arcmap里,a1、a0、b1、b0从属性表可读出,s用raster calculator配合con()函数不难求出。
kappa计算结果为-1~1,但通常kappa是落在 0~1 间,可分为五组来表示不同级别的一致性:0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)。
spearman相关系数

对不服从正态分布的资料、原始资料等级资料、一侧开口资料、总体分布类型未知的资料不符合使用积矩相关系数来描述关联性。此时可采用秩相关(rank correlation),也称等级相关,来描述两个变量之间的关联程度与方向。
计算步骤:
⑴编秩:将两变量X、Y成对的观察值分别从小到大顺序编秩,用pi表示xi的秩次;用qi表示yi的秩次。若观察值相同取平均秩次。
⑵将秩次带入公式计算:
⑶由样本算得的秩相关系数是否有统计学意义,应作假设检验。
检验编辑
⑴建立假设检验,确定检验水准:
: , :
⑵计算检验统计量:
查秩相关系数界值表,若 超过界值表,则拒绝 ; 作 检验。
以上是关于利用SPSS进行一致性检验并计算Kappa值的主要内容,如果未能解决你的问题,请参考以下文章
一致性检验的三种方式--ICCkappaweighted kappa