变分(Calculus of variations)的概念及运算规则
Posted teengad
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了变分(Calculus of variations)的概念及运算规则相关的知识,希望对你有一定的参考价值。
文章目录
1. 回顾:微分的定义
在介绍变分之前,首先回顾微分的定义:
当自变量 x → x + d x x\\rightarrow x+\\mathrmdx x→x+dx 时,相应的因变量 y → y + d y y\\rightarrow y+\\mathrmdy y→y+dy。
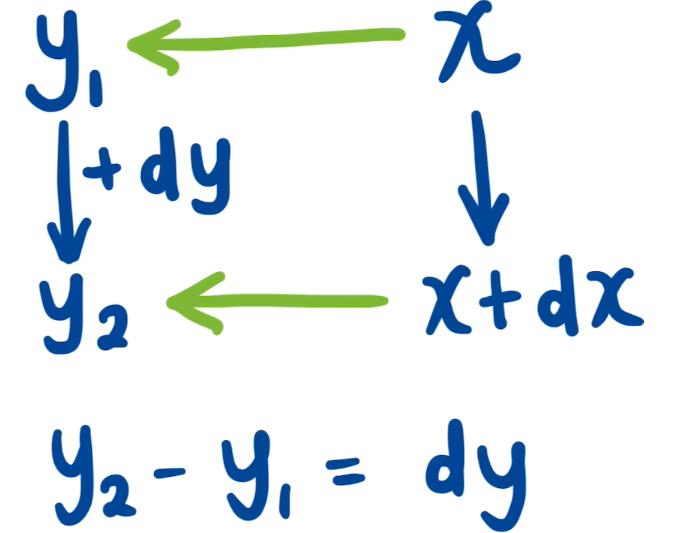
则此时 d y \\mathrmdy dy 就是函数 y ( x ) y(x) y(x) 的微分了。下面为上述过程的图示:
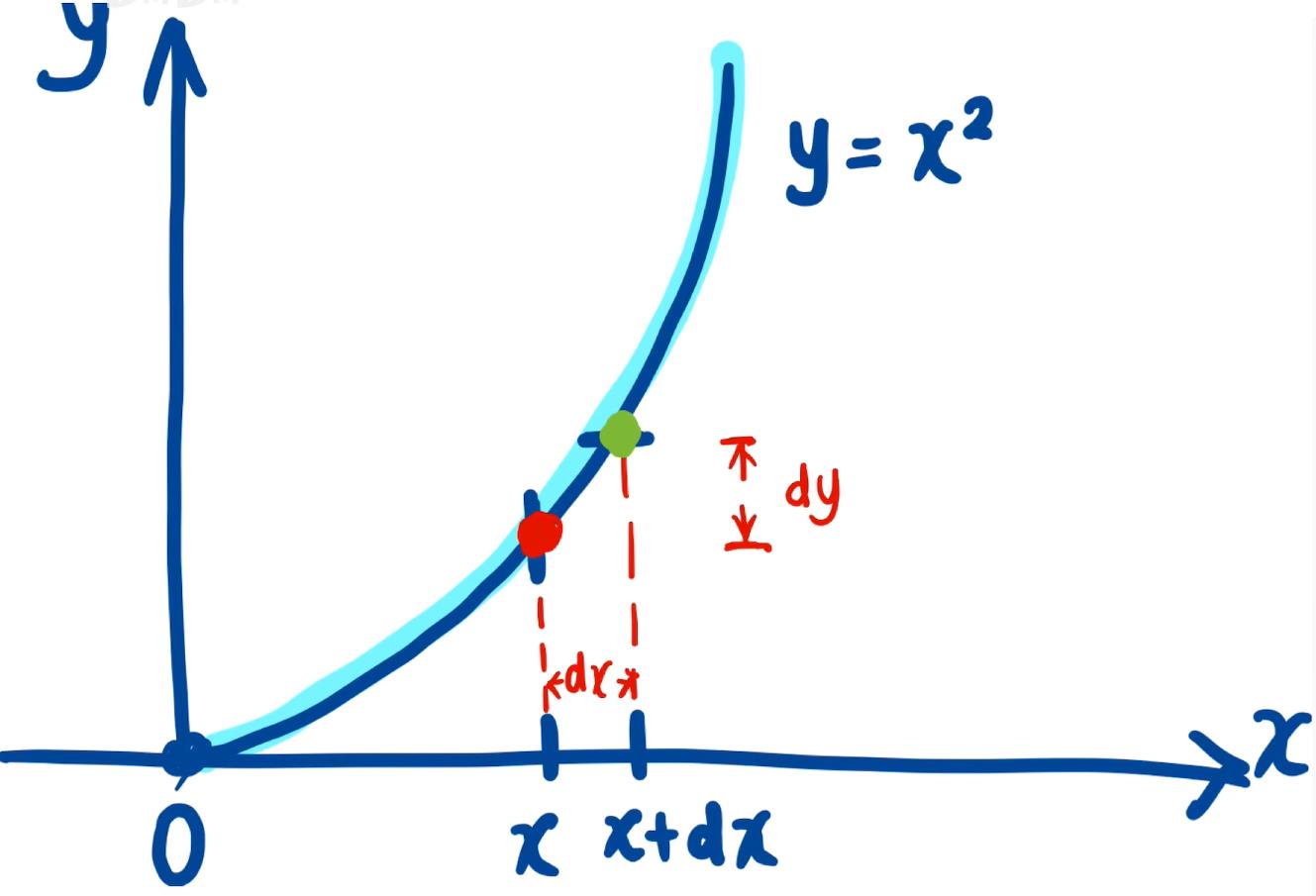
2. 泛函和变分概念简介
2.1 泛函概念简介
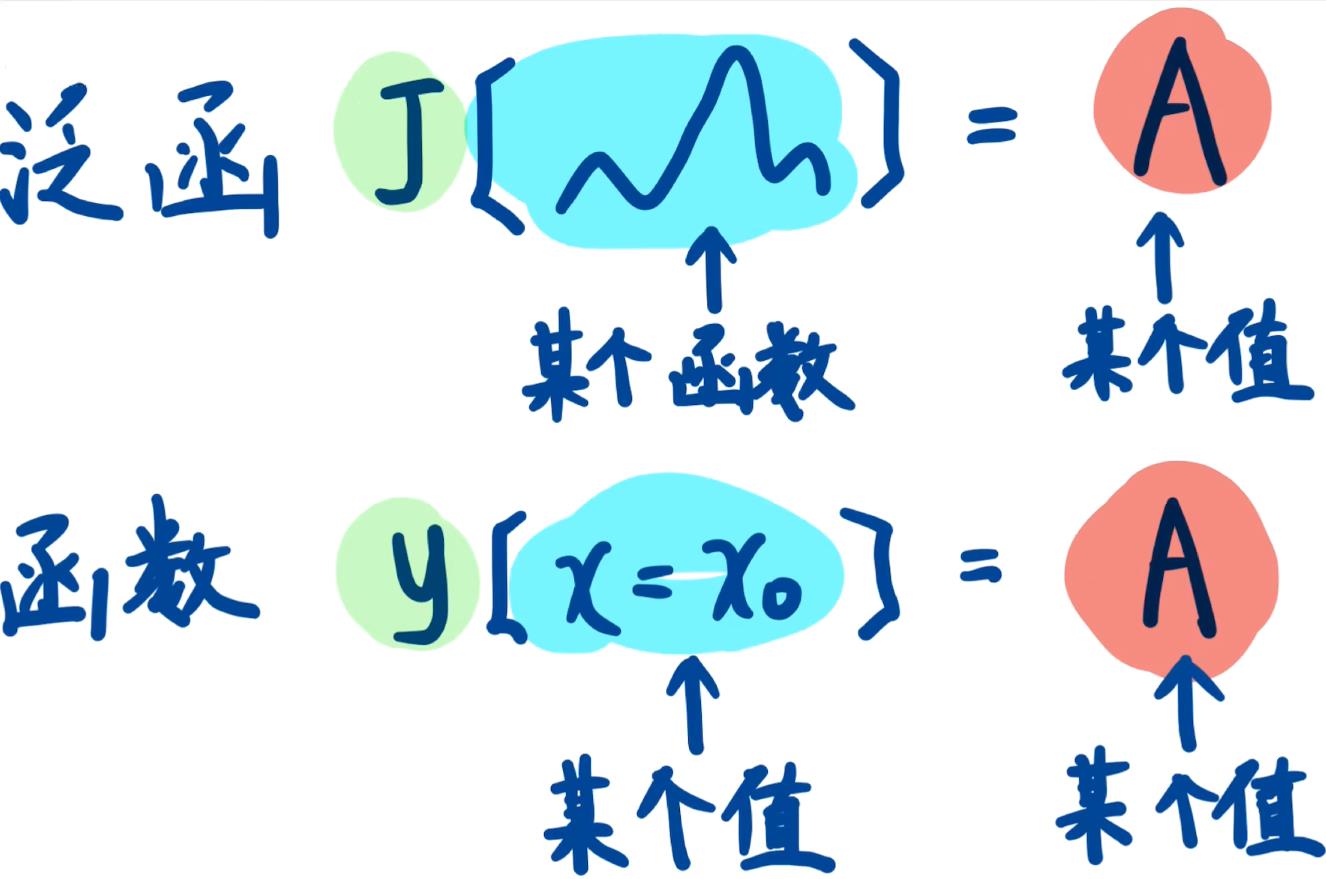
泛函为函数的函数,
2.2 变分概念简介
通过上面的介绍,那么问题来了,如何用同样的思路去研究泛函的变化?通过类比推广, x x x 的变化,可以推广为函数的变形:
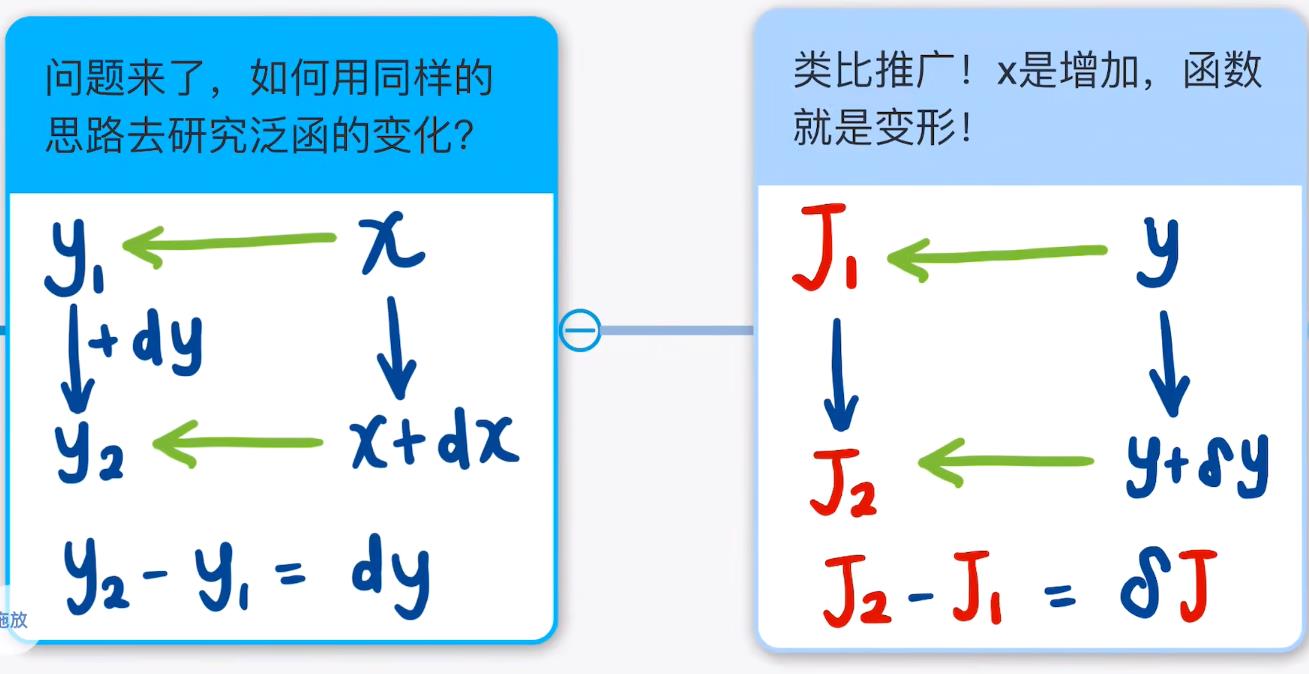
那么函数的变形如何理解呢?如下图:
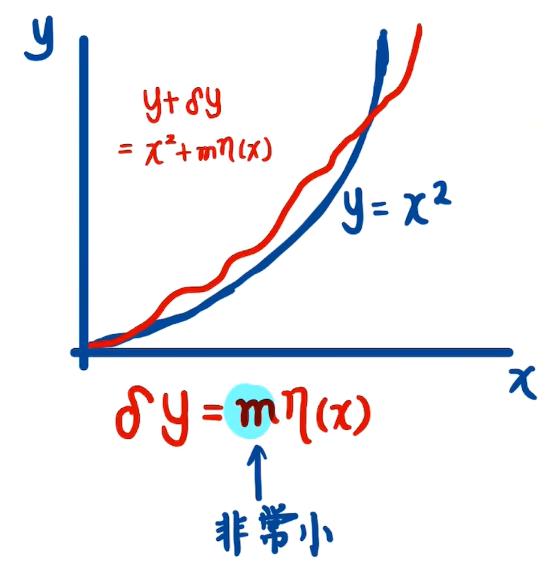
我们可以把原先的函数作一点点形变,即可以在原先的函数上加上一个任意函数 η ( x ) \\eta(x) η(x),然后在任意函数的前面乘上非常小或者足够小的系数 m m m,此时我们就可以把 y = x 2 y=x^2 y=x2(仅举例,可以推广)和新函数 y + δ y = x 2 + m η ( x ) y+\\mathtt\\delta y=x^2+m\\eta(x) y+δy=x2+mη(x) 的差导致的泛函 J J J 的变化 J 2 − J 1 = δ J J_2-J_1=\\delta J J2−J1=δJ 就是泛函 J J J 的变分。
这个泛函的变分的线性化表示是整个变分中最重要的一步!同理,在微积分中,使用线性化的思想处理问题也是处理所有其他问题的前提!
下面是泛函变分的示意图:
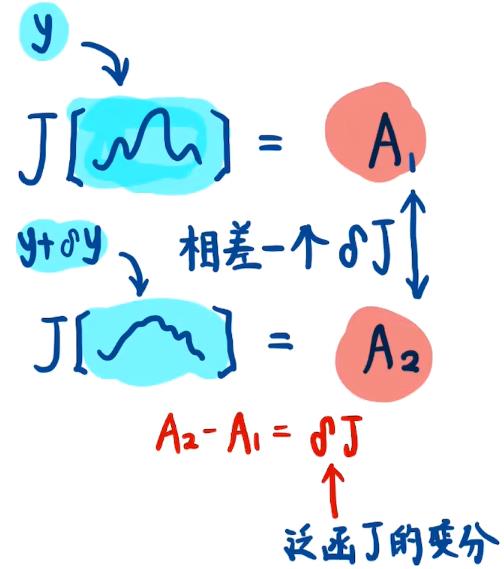
3. 变分的运算法则简介
变分和微分的运算法则在很多情况下都是相同的,可以直接把微分的运算法则拿过来用就可以了:
- 复合函数链式法则
d y ( x ) = y ′ ( x ) d x ⇓ δ y ( x ) = y ′ ( x ) δ x \\mathrmdy(x)=y'(x)\\mathrmdx\\\\ \\Downarrow\\\\ \\delta y(x)=y'(x)\\delta x dy(x)=y′(x)dx⇓δy(x)=y′(x)δx
- 四则运算(乘法运算)
d ( A B ) = B d A + A d B ⇓ δ ( A B ) = B δ A + A δ B \\mathrmd(AB)=B\\mathrmdA+A\\mathrmdB\\\\ \\Downarrow\\\\ \\delta (AB)=B\\delta A+A\\delta B\\\\ d(AB)=BdA+AdB⇓δ(AB)=BδA+AδB
- 全微分
d Z = ∂ Z ∂ x d x + ∂ Z ∂ y d y ⇓ δ Z = ∂ Z ∂ x δ x + ∂ Z ∂ y δ y \\mathrmd Z=\\frac\\partial Z\\partial x\\mathrmd x+\\frac\\partial Z\\partial y\\mathrmd y\\\\ \\Downarrow\\\\ \\delta Z=\\frac\\partial Z\\partial x\\delta x+\\frac\\partial Z\\partial y\\delta y dZ=∂x∂Zdx+∂y∂Zdy⇓δZ=∂x∂Zδx+∂y∂Zδy
- 假设下图方框里有一串表达式,然后乘上 δ y \\delta y δy等于0,由于 δ y \\delta y δy可以随意变动,则只能使得方框里的表达式为0;
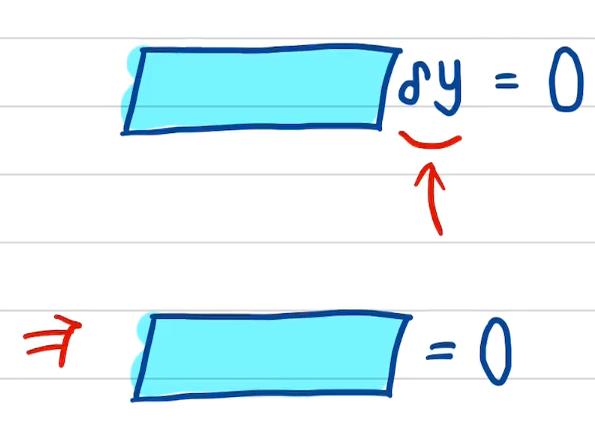
- 变分运算符号可以与积分运算、微分运算、偏导数符号调换位置。

4. 变分法详述
变分微积分,或变分法(Calculus of Variations or variational method)是一个数学分析领域,它使用变分(函数和泛函的微小变化)来找到泛函的最大值和最小值:从一组函数到实数的映射。泛函通常表示为涉及函数及其导数的定积分。使用变分法的欧拉-拉格朗日方程可以找到最大化或最小化泛函的函数。
变分法是 17 世纪末发展起来的一门数学分支,是处理泛函的数学领域,和处理数的函数的普通微积分相对。它最终寻求的是极值函数:它们使得泛函取得极大或极小值。变分法起源于一些具体的物理学问题,最终由数学家研究解决。有些曲线上的经典问题采用这种形式表达:一个例子是最速降线,在重力作用下一个粒子沿着该路径可以在最短时间从点 A 到达不直接在它底下的一点 B。在所有从 A 到 B 的曲线中,必须极小化代表下降时间的表达式。
另外还有找到连接两点的最短长度曲线。如果没有约束,则解是点之间的直线。但是,如果曲线被限制在空间表面上,那么解决方案就不太明显,并且可能存在许多解决方案。这种解决方案被称为测地线。费马原理提出了一个相关问题:光遵循连接两点的最短光程路径,这取决于介质的材料。力学中一个对应的概念是最小/静止作用原理。
4.1 历史
可以说变分法始于 1687 年牛顿的最小阻力问题,随后是约翰·伯努利 (Johann Bernoulli)(1696 年)提出的短时线问题。它立即引起了雅各布·伯努利(Jakob Bernoulli)和 Marquis de l’Hôpital 的注意,但莱昂哈德·欧拉(Leonhard Euler)从 1733 年开始首先阐述了这个主题。拉格朗日受到欧拉工作的影响,对这一理论做出了重大贡献。在欧拉看到 19 岁的拉格朗日 1755 年的作品后,欧拉放弃了他自己的部分几何方法,转而支持拉格朗日的纯分析方法,并在他 1756 年的讲座 “Elementa Calculi Variationum” 中将这个主题重新命名为变分法。
勒让德 (Legendre) (1786) 制定了一种方法,但并不完全令人满意,用于区分最大值和最小值。艾萨克·牛顿和戈特弗里德·莱布尼茨也对这个主题给予了一些早期的关注。在这其中,文森佐·布鲁纳奇 (Vincenzo Brunacci) (1810)、卡尔·弗里德里希·高斯 (Carl Friedrich Gauss) (1829)、西蒙·泊松 (Siméon Poisson) (1831)、米哈伊尔·奥斯特罗格拉茨基 (Mikhail Ostrogradsky) (1834) 和卡尔·雅可比 (Carl Jacobi) (1837) 都是贡献者。 Sarrus (1842) 的一项重要的综合性工作是由 Cauchy (1844) 浓缩和改进的。 Strauch (1849)、Jellett (1850)、Otto Hesse (1857)、Alfred Clebsch (1858) 和 Lewis Buffett Carll (1885) 撰写了其他有价值的论文和回忆录,但也许本世纪最重要的著作是维尔斯特拉斯(Weierstrass)。他著名的理论课程是划时代的,可以说他是第一个将其建立在坚实和不容置疑的基础上的人。1900 年发表的第 20 和第 23 希尔伯特问题鼓励了进一步的发展。
在 20 世纪,David Hilbert、Oskar Bolza、Gilbert Ames Bliss、Emmy Noether、Leonida Tonelli、Henri Lebesgue 和 Jacques Hadamard 等做出了重大贡献。Marston Morse 在现在所谓的 Morse 理论中应用了变分法。Lev Pontryagin、Ralph Rockafellar 和 F. H. Clarke 为最优控制理论中的变分微积分开发了新的数学工具。Richard Bellman 的动态规划是变分法的替代方法。
4.2 极值
变分法与泛函的最大值或最小值(统称为极值)有关。泛函将函数映射到标量,因此泛函被描述为“函数的函数”。泛函对于定义在给定域上的给定函数空间的元素 y y y 具有极值。一个泛函 J [ y ] J[y] J[y] 如果 Δ J = J [ y ] − J [ f ] \\Delta J=J[y]-J[f] ΔJ=J[y]−J[f] 对于 f f f 的任意小的邻域中的所有 y y y 具有相同的符号。函数 f f f 称为极值函数或极值。如果在 f f f 的任意小邻域中处处 Δ J ≤ 0 \\Delta J\\leq 0 ΔJ≤0,则 J [ f ] J[f] J[f] 被称为局部极大值,相反,如果 Δ J ≥ 0 \\Delta J\\geq 0 ΔJ≥0,则称为局部极小值。对于连续函数的函数空间,对应的泛函的极值称为强极值或弱极值,这取决于连续函数的一阶导数是否都是连续的。
泛函的强极值和弱极值都是针对连续函数空间的,但强极值还有一个额外的要求,即空间中函数的一阶导数是连续的。因此,强极值也是弱极值,但反过来可能不成立。找到强极值比找到弱极值更难。用于寻找弱极值的必要条件的一个例子是欧拉-拉格朗日方程(Euler-Lagrange equation)。
5. 变分的运算法则详述
在变分法中,泛函导数(或变分导数) 将泛函的变化与泛函所依赖的函数的变化联系起来。
在变分法中,泛函通常用函数、它们的参数和它们的导数的积分来表示。在泛函的积分 L L L 中,如果函数 f f f 通过添加另一个任意小的函数 δ f \\delta f δf 来改变,并且所得被积函数以 δ f \\delta f δf 的幂展开,则一阶项中 δ f \\delta f δf 的系数称为泛函导数。
例如,考虑泛函:
J [ f ] = ∫ a b L ( x , f ( x ) , f ′ ( x ) ) d x J[f]=\\int _a^bL(x,f(x),f'(x)\\,)\\,\\mathrmdx J[f]=∫abL(x,f(x),f′(x))dx
其中 f ′ ( x ) ≡ d f / d x f'(x)\\equiv\\mathrmdf/\\mathrmdx f′(x)≡df/dx。如果通过向其添加函数 δ f \\delta f δf 来改变 f f f(注意此时 x x x 相对不变),并且将得到的被积函数 L ( x , f + δ f , f ′ + δ f ′ ) L(x,f+\\delta f,f'+\\delta f') L(x,f+δf,f′+δf′) 以 δ f \\delta f δf 的幂展开,则 J J J 的值在 δ f \\delta f δf 中的一阶变化可表示为:
δ
J
=
∫
a
b
(
∂
L
∂
f
δ
f
(
x
)
+
∂
L
∂
f
′
d
d
x
δ
f
(
x
)
)
d
x
=
∫
a
b
(
∂
L
∂
f
−
d
d
x
∂
L
∂
f
′
)
δ
f
(
x
)
d
x
+
∂
L
∂
f
′
(
b
)
δ
f
(
b
)
−
∂
L
∂
f
′
(
a
)
δ
f
(
a
)
\\beginaligned \\delta J &=\\int _a^b\\left(\\frac \\partial L\\partial f\\delta f(x)+\\frac \\partial L \\partial f'\\frac \\mathrmd\\mathrmdx\\delta f(x)\\right)\\,\\mathrmdx\\\\ &=\\int _a^b\\left(\\frac \\partial L\\partial f-\\frac \\mathrmd\\mathrmdx\\frac \\partial L\\partial f'\\right)\\delta f(x)\\,\\mathrmdx\\,+\\,\\frac \\partial L\\partial f'(b)\\delta f(b)\\,-\\,\\frac \\partial L\\partial f'(a)\\delta f(a) \\endaligned
δJ=∫aCalculus of Variations:变分计算
泛函
泛函(functional)指以函数构成的向量空间为定义域,实数为值域为的“函数”,即某一个依赖于其它一个或者几个函数确定其值的量,往往被称为“函数的函数”。
函数代表了数到数的映射,而泛函代表了函数到数的映射,即给定一个函数,泛函能够得到一个数
欧拉-拉格朗日方程
求解以积分形式表示的量的最小化或者最大化
当泛函 取极值时,函数
y
(
x
)
y(x)
y(x)应当满足欧拉-拉格朗日方程:
∂
∂
y
F
(
x
,
y
,
y
x
)
−
d
d
x
(
∂
∂
y
x
F
(
x
,
y
,
y
x
)
)
=
0
\\frac \\partial \\partial yF(x,y,y_x)-\\frac ddx(\\frac \\partial \\partial y_xF(x,y,y_x))=0\\\\
∂y∂F(x,y,yx)−dxd(∂yx∂F(x,y,yx))=0
简单证明:
设存在泛函:
J
(
y
)
=
∫
a
b
F
(
x
,
y
,
y
x
)
J(y) = \\int_a^bF(x,y,y_x)
J(y)=∫abF(x,y,yx)
我们假设能够使
J
(
y
)
J(y)
J(y) 取得极值的函数
y
y
y 为
u
(
x
)
u(x)
u(x) 。那么在区间
[
a
,
b
]
[a,b]
[a,b] 上,定义函数族
y
(
x
)
=
u
(
x
)
+
ϵ
η
(
x
)
y(x)=u(x)+\\epsilon\\eta(x)
y(x)=u(x)+ϵη(x)
其中
ϵ
\\epsilon
ϵ 是一个实参数,
η
(
x
)
\\eta(x)
η(x) 定义为函数
y
(
x
)
y(x)
y(x) 与
u
(
x
)
u(x)
u(x) 的差值。由此可以看出
η
(
x
)
\\eta(x)
η(x) 应当满足
η
(
a
)
=
η
(
b
)
=
0
\\eta(a)=\\eta(b)=0
η(a)=η(b)=0 ,那么
y
(
x
)
y(x)
y(x) 当然也满足边界条件,也代表两点之间的一条路径,并且在确定的
η
(
x
)
\\eta(x)
η(x) 下,其函数表达式只与 ϵ 有关。
那么对于任意确定的函数 η ( x ) \\eta(x) η(x), 泛函 J ( y ) = J ( u + ϵ η ) = J ( ϵ ) J(y)=J(u+\\epsilon\\eta)=J(\\epsilon) J(y)=J(u+ϵη)=J(ϵ) ,应当只是参数 ϵ \\epsilon ϵ 的函数,且 d J ( ϵ ) d ϵ ∣ ϵ = 0 \\frac dJ(\\epsilon)d\\epsilon|_\\epsilon=0 dϵdJ(ϵ)∣ϵ=0( ϵ = 0 \\epsilon=0 ϵ=0 时, y ( x ) = u ( x ) y(x)=u(x) y(x)=u(x) ,泛函 J ( y ) J(y) J(y) 取极值)。
为了要满足上面的条件
d
J
(
ϵ
)
d
ϵ
∣
ϵ
=
0
\\frac dJ(\\epsilon)d\\epsilon|_\\epsilon=0
dϵdJ(ϵ)∣ϵ=0,我们首先来计算在任意确定的
η
(
x
)
\\eta(x)
η(x)的情况下计算
d
J
(
ϵ
)
d
ϵ
\\frac dJ(\\epsilon)d\\epsilon
dϵdJ(ϵ)
d
J
(
ϵ
)
d
ϵ
=
d
d
ϵ
∫
a
b
F
(
x
,
y
,
y
x
)
d
(
x
)
=
∫
a
b
∂
F
(
x
,
y
,
y
x
)
∂
ϵ
d
(
x
)
=
∫
a
b
∂
F
∂
y
∂
y
∂
ϵ
+
∂
F
∂
y
x
∂
y
x
∂
ϵ
d
(
x
)
(
链式求导
)
=
∫
a
b
∂
F
∂
y
η
(
x
)
+
∂
F
∂
y
x
η
′
(
x
)
d
(
x
)
(
η
′
(
x
)
=
d
η
(
x
)
/
d
x
)
=
∫
a
b
∂
F
∂
y
η
(
x
)
+
∂
F
∂
y
x
d
η
(
x
)
=
∫
a
b
∂
F
∂
y
η
(
x
)
+
η
(
x
)
∂
F
∂
y
x
∣
a
b
−
∫
a
b
d
d
x
(
∂
F
∂
y
x
)
η
(
x
)
d
x
(
分部积分
)
=
∫
a
b
[
∂
F
∂
y
−
d
d
x
(
∂
F
∂
y
x
)
]
η
(
x
)
d
x
(
η
(
a
)
=
η
(
b
)
=
0
)
\\beginalign \\frac dJ(\\epsilon)d\\epsilon & =\\frac dd\\epsilon\\int_a^bF(x,y,y_x)d(x)\\\\ &=\\int_a^b\\frac \\partial F(x,y,y_x)\\partial\\epsilond(x)\\\\ &=\\int_a^b\\frac \\partial F\\partial y\\frac \\partial y\\partial\\epsilon + \\frac \\partial F\\partial y_x\\frac \\partial y_x\\partial\\epsilon d(x)\\qquad(链式求导)\\\\ &=\\int_a^b\\frac \\partial F\\partial y\\eta(x) + \\frac \\partial F\\partial y_x\\eta'(x) d(x)\\qquad(\\eta'(x)=d\\eta(x)/dx)\\\\ &=\\int_a^b\\frac \\partial F\\partial y\\eta(x) + \\frac \\partial F\\partial y_x d\\eta(x)\\\\ &=\\int_a^b\\frac \\partial F\\partial y\\eta(x) + \\eta(x)\\frac \\partial F\\partial y_x\\big|_a^b-\\int_a^b\\frac ddx(\\frac \\partial F\\partial y_x)\\eta(x)dx\\qquad (分部积分)\\\\ &=\\int_a^b[\\frac \\partial F\\partial y -\\frac ddx(\\frac \\partial F\\partial y_x)]\\eta(x)dx\\qquad(\\eta(a)=\\eta(b)=0)\\\\ \\endalign
dϵdJ(ϵ)=dϵd∫abF(x,y,yx)d(x)=∫ab∂ϵ∂F(x,y,yx)d(x)=∫ab∂y∂F∂ϵ∂y+∂yx∂F∂ϵ∂yCalculus of Variations:变分计算
机器学习-白板推导系列(三十二)-变分自编码器(VAE,Variational AutoEncoder)
变分自编码器(Variational Autoencoder, VAE)通俗教程