机器学习-白板推导系列(三十二)-变分自编码器(VAE，Variational AutoEncoder)
Posted Paul-Huang
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习-白板推导系列(三十二)-变分自编码器(VAE，Variational AutoEncoder)相关的知识，希望对你有一定的参考价值。
1. Introduction
本小节主要介绍的是 变 分 自 编 码 器 （ V a r i a t i o n a l A u t o E n c o d e r ） \\color{red}变分自编码器（Variational\\;AutoEncoder） 变分自编码器（VariationalAutoEncoder），VAE在之前的变分推断中就有介绍，具体在“随机梯度变分推断（SGVI）”中已进行描述。其中采用了重参数化技巧，也就是Amortized Inference。VAE在很多blog中都有详细的解释，这里只是很简单的描述其思想，希望可以抛转引玉。
VAE中的V指的是变分推断，这个概念是来自于概率图模型。而AE的概念是来自于神经网络。所以，VAE实际上是神经网络和概率图的结合模型。
2. 从GMM到VAE
VAE是一个Latent Variable Model（LVM）。我们之前介绍的最简单的LVM是高斯混合模型（GMM），那么GMM是如何一步一步演变成VAE的呢？GMM是k个高斯分布（Gaussian Dist）的混合，而VAE的思想是无限(infinite)个Gaussian Dist的混合。在GMM中， Z ∼ Z\\sim Z∼ Categorical Distribution(1维离散型分布)，如下表所示，
| Z | C 1 C_1 C1 | C 2 C_2 C2 | ⋯ \\cdots ⋯ | C k C_k Ck |
|---|---|---|---|---|
| P ( Z ) P(Z) P(Z) | p 1 p_1 p1 | p 2 p_2 p2 | ⋯ \\cdots ⋯ | p k p_k pk |
其中 ∑ i = 1 k p i = 1 \\sum_{i=1}^k p_i = 1 ∑i=1kpi=1，在给定 Z = C k Z=C_k Z=Ck的情况下，满足 P ( X ∣ Z = C i ) ∼ N ( μ i , ∑ i ) P(X|Z=C_i)\\sim \\mathcal{N}(\\mu_i, \\sum_i) P(X∣Z=Ci)∼N(μi,∑i)。
很容易可以感觉到，这个GMM顶多就用来做一做聚类分布，复杂的任务根本做不了。比如，目标检测，GMM肯定就做不了，因为 Z Z Z只是离散的类别，它太简单了。
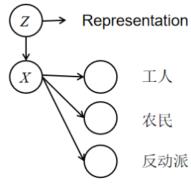
下面举一个例子，假设
X
X
X是人民群众，我们想把他们分成工人，农民和反动派。由于，
Z
Z
Z是一个一维的变量，那么我们获得的特征就很有限，所以分类就很简单。
那么，怎样才可以增加
Z
Z
Z的特征信息呢？因为
Z
Z
Z是离散的一维的隐变量，那么把它扩展成离散的高维的随机变量，不就行了。那么，变化就来了，大家看好了。GMM中
Z
Z
Z是离散的一维变量，那么在VAE被扩展为
m
m
m维的高斯分布
Z
∼
N
(
0
,
I
m
×
m
)
Z\\sim \\mathcal{N}(0,I_{m\\times m})
Z∼N(0,Im×m)。而在给定
Z
Z
Z的条件下，
P
(
X
∣
Z
)
∼
N
(
μ
θ
(
Z
)
,
∑
θ
(
Z
)
)
P(X|Z)\\sim \\mathcal{N}(\\mu_{\\theta}(Z),\\sum_{\\theta}(Z))
P(X∣Z)∼N(μθ(Z),∑θ(Z))。这里采用神经网络来逼近均值和方差，而不通过重参数化技巧这些直接去算（太麻烦了）。那么均值和方差是一个以
Z
Z
Z为自变量，
θ
\\theta
θ为参数的函数。那么，假设条件可以总结为：
{
Z
∼
N
(
0
,
I
m
×
m
)
P
(
X
∣
Z
)
∼
N
(
μ
θ
(
Z
)
,
∑
θ
(
Z
)
)
(1)
\\begin{aligned} \\left\\{ \\begin{array}{ll} Z\\sim \\mathcal{N}(0,I_{m\\times m}) & \\\\ P(X|Z)\\sim \\mathcal{N}(\\mu_{\\theta}(Z),\\sum_{\\theta}(Z)) & \\end{array}\\right.\\end{aligned}\\tag{1}
{Z∼N(0,Im×m)P(X∣Z)∼N(μθ(Z),∑θ(Z))(1)
其中
Z
∼
N
(
0
,
I
m
×
m
)
Z\\sim \\mathcal{N}(0,I_{m\\times m})
Z∼N(0,Im×m)是一个先验分布假设，
Z
Z
Z服从怎样的先验分布都没有关系，只要是高维的连续的就行了，只是在这里假设为Gaussian。我们关心的不是先验，我们实际上关心的是后验
P
(
Z
∣
X
)
P(Z|X)
P(Z∣X)，
Z
Z
Z实际上只是帮助我们建模的。那么，接下来可以做一系列的推导：
P
θ
(
X
)
=
∫
Z
P
θ
(
X
,
Z
)
d
Z
=
∫
Z
P
(
Z
)
P
θ
(
X
∣
Z
)
d
Z
(2)
\\begin{aligned} P_\\theta(X) = \\int_Z P_\\theta(X,Z)dZ = \\int_Z P(Z)P_\\theta(X|Z) dZ \\end{aligned}\\tag{2}
Pθ(X)=∫ZPθ(X,Z)dZ=∫ZP(Z)Pθ(X∣Z)dZ(2)
推导到了这里有个什么问题呢？因为
Z
Z
Z是一个高维的变量，所以
∫
z
P
(
Z
)
P
θ
(
X
∣
Z
)
d
Z
\\int_z P(Z)P_\\theta(X|Z) dZ
∫zP(Z)Pθ(X∣Z)dZ是intractable，积分根本算不出来。由于，
P
θ
(
X
)
P_\\theta(X)
Pθ(X)是intractable，直接导致
P
θ
(
Z
∣
X
)
P_\\theta(Z|X)
Pθ(Z∣X)也算不出来。因为根据Bayesian公式，
P
θ
(
Z
∣
X
)
=
P
θ
(
Z
)
P
θ
(
X
∣
Z
)
P
θ
(
X
)
(3)
\\begin{aligned} P_\\theta(Z|X) = \\frac{P_\\theta(Z)P_\\theta(X|Z)}{P_\\theta(X)} \\end{aligned}\\tag{3}
Pθ(Z∣X)=Pθ(X)Pθ(Z)Pθ(X∣Z)机器学习-白板推导系列(三十一)-生成对抗网络(GAN，Generative Adversarial Network)