pytorch的基本架构

Posted 2023-03-24

参考技术A 主要由一个控制整个模块功能的torch.nn组成。其中含有一个包含大量计算方法的nn.functional和全部层需要定义的nn.Module。

这是整个torch的核心所在。这是一个非常特殊的类。我们暂时来看他的使用和外在的表现。其主要由一个通过self点什么self点什么的变量定义过程的初始化函数和一个继承过来本身就具有大量功能的forward函数组成。我们任何时候在使用nn.Moduel继承下来一个新类后，都只要再通过函数的多态性重写其forword函数即可完成我们需要的功能。也就是说在继承下来的初始化函数里写上self点 层名字 。然后在forward里写上哪层去哪层就行了。

然后

就可以看到每一层参数的shape。同样debug后就发现par里有data参数，里面就存放了这一层当前训练后的所有参数。并且是以tensor形式存放的，卷积的就是一个tansor，全连接的除了一个weight的tensor还有一个bias的tensor。这时候你还会发现，他的模式是cpu模式的。

强化学习系列13：基于pytorch的框架“天授”

1. 基本架构

1.1 架构图

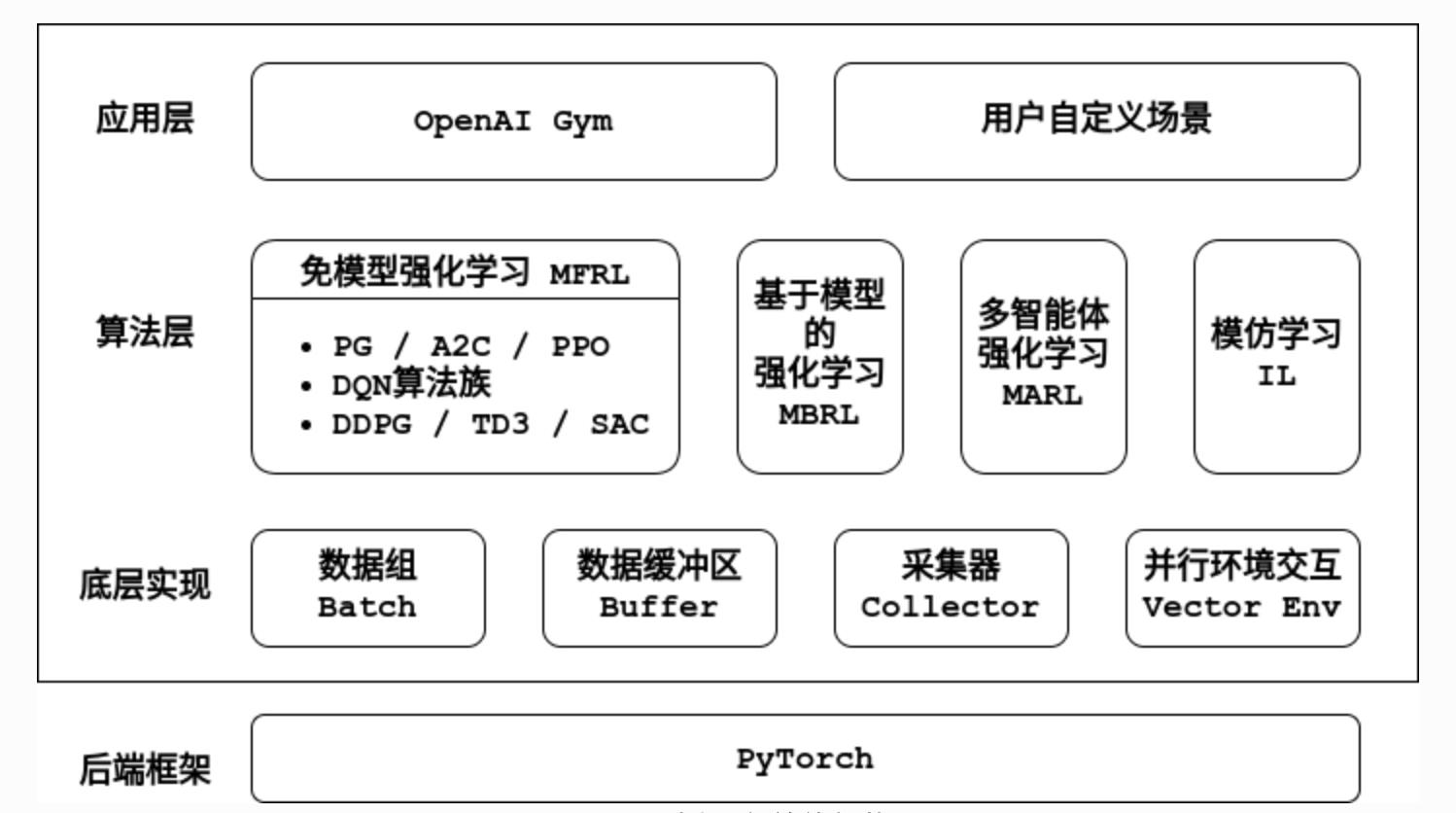
底层实现的关系如下：

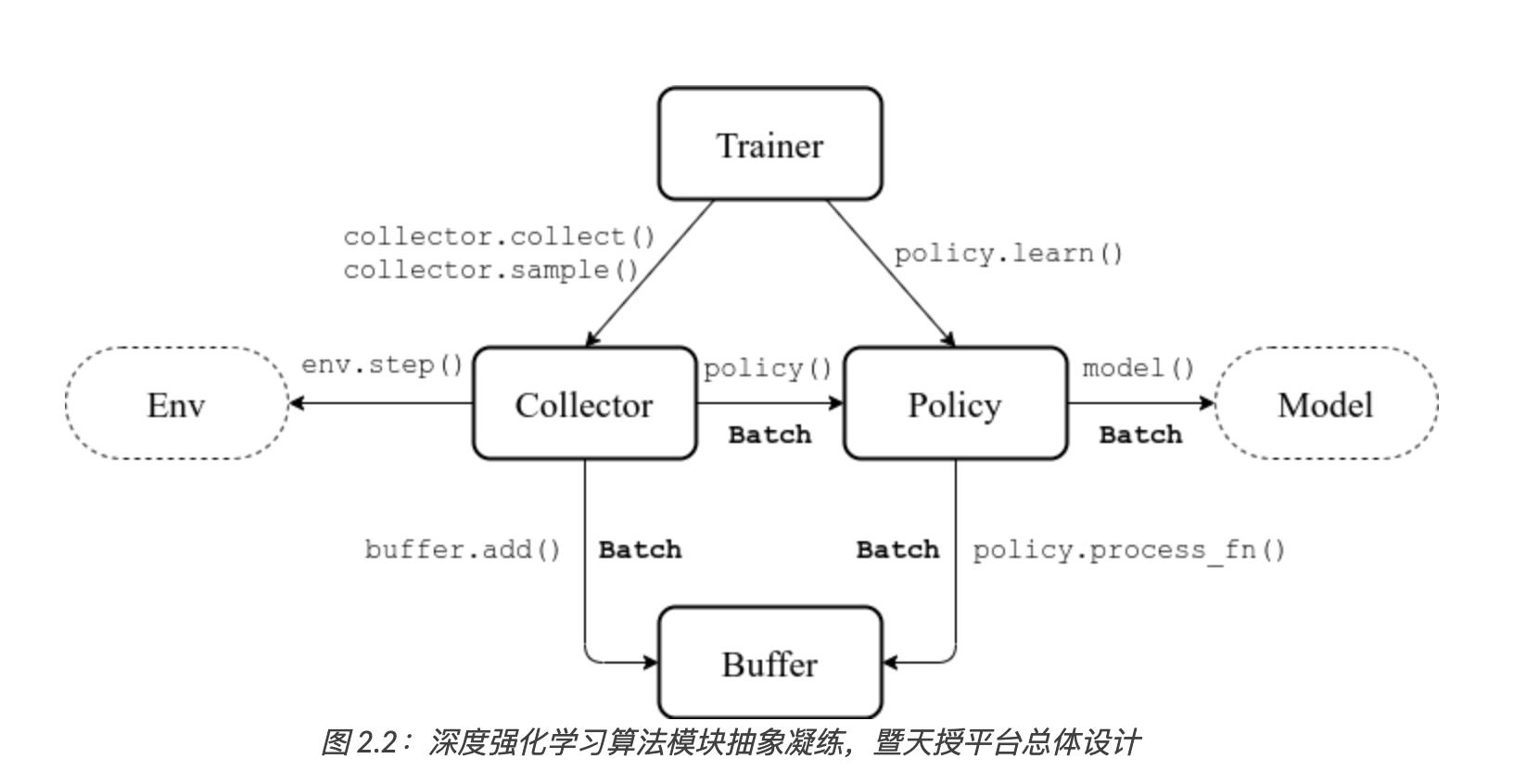
1.2 组件介绍（重要）

1.2.1 数据组（Batch）

数据组是平台内部各个模块之间传递数据的基本数据结构。
它支持任意关键字初始化、对任意元素进行修改，以及嵌套调用和格式化输出的功能。如果数据组内各个元素值的第0维大小相等，还可支持切分（split）操作。数据组保留了如下7个关键字：

obs：t 时刻的观测值 $o_t$；
act： t 时刻策略采取的动作值 $a_t$；
rew： t 时刻环境反馈的奖励值 $r_t$；
done： t 时刻环境结束标识符 d t ∈ { 0 , 1 } d_t\\in\\{0,1\\} dt​∈{0,1}，0为未结束，1为结束；
obs_next： t+1 时刻的观测值 $o_{t+1}$；
info： t 时刻环境给出的环境额外信息 $i_t$，以字典形式存储；
policy： t 时刻策略在计算过程中产生的数据 $p_t$。

1.2.2 数据缓冲区（Buffer）

数据缓冲区存储策略与环境交互产生的数据。在采样时，如果传入大小是0，则返回整个缓冲区中的所有数据，以支持在同略学习算法的训练需求。

目前数据缓冲区的类型有：最基本的重放缓冲区（Replay Buffer），使用列表作为底层数据结构的列表缓冲区（List Replay Buffer）、优先级经验重放缓冲区（Prioritized Replay Buffer）支持优先权重采样。此外数据缓冲区还支持历史数据堆叠采样（例如给定采样时间下标 t 和堆叠帧数 n ，返回堆叠的观测值 { o t − n + 1 , … , o t } ） \\{o_{t-n+1}, \\dots, o_t\\} ） {ot−n+1​,…,ot​}）和多模态数据存储（需要存储的数据可以是一个字典）。

1.2.3 环境（Env）

环境接口遵循OpenAI Gym定义的通用接口，即每次调用 step 函数时，需要输入一个动作 $a_t$ ，返回一个四元组：下一个观测值 $o_{t+1}$、这个时刻采取动作值 $a_t$所获得的奖励 $r_t$ 、环境结束标识符 $d_t$ 、以及环境返回的其他信息 $i_t$ 。

为使所有强化学习算法支持并行环境采样，天授封装了几个不同的向量化环境类，以第0个维度来区分是哪个环境产生的数据。

1.2.4 策略（Policy）

策略是强化学习算法的核心。智能体除了需要做出决策，还需不断地学习来自我改进。包括4个模块：
__init__：策略的初始化，比如初始化自定义的模型（Model）、创建目标网络（Target Network）等；
forward：从给定的观测值 $o_t$ 中计算出动作值 $a_t$，对应Policy到Model的调用和Collector到Policy的调用；
process_fn：在获取训练数据之前和数据缓冲区进行交互，对应Policy到Buffer的调用；
learn：使用一个数据组进行策略的更新训练，中对应Trainer到Policy的调用。

1.2.5 模型（Model）

模型为策略的核心部分。为了支持任意神经网络结构的定义，天授只是规定了模型与策略进行交互的接口，从而让用户有更大的自由度编写代码和训练逻辑。模型的接口定义如下：

• 输入：
  obs：观测值，可以是NumPy数组、torch张量、字典、或者是其他自定义的类型；
  state：隐藏状态表示，为RNN使用，可以为字典、NumPy数组、torch张量；
  info：环境信息，由环境提供，是一个字典；

• 输出
  logits：网络的原始输出，被策略用于计算动作值；比如在DQN [MKS+15] 算法中 logits 可以为动作值函数，在PPO [SWD+17] 中如果使用对角高斯策略，则 logits 可以为 ($\mu ,\sigma$) 的二元组；

• state：下一个时刻的隐藏状态，为RNN使用；

• policy：策略输出的中间值，会被存储至重放缓冲区中，用于后续训练时使用。

1.2.6 采集器（Collector）

采集器定义了策略与环境交互的过程。采集器主要包含以下两个函数：

• collect：让给定的策略和环境交互 至少 $n_s$ 步、或者至少 $n_e$ 轮，并将交互过程中产生的数据存储进数据缓冲区中；
• sample：从数据缓冲区中采集出给定大小的数据组，准备后续的策略训练。

为了支持并行环境采样，采集器采用了缓存数据缓冲区，即同时和多个环境进行交互并将数据存储在对应的缓存区中，一旦有一个环境的交互结束，则将对应缓存区的数据取出，存放至主数据缓冲区中。由于无法精确控制环境交互的结束时间，采集的数据量有可能会多于给定数值，因此在采集中此处强调“至少”。

采集器理论上还可以支持多智能体强化学习的交互过程，将不同的数据缓冲区和不同策略联系起来，即可进行交互与数据采样。

1.2.7 训练器（Trainer）

训练器负责最上层训练逻辑的控制，例如训练多少次之后进行策略和环境的交互。现有的训练器包括同策略学习训练器（On-policy Trainer）和异策略学习训练器（Off-policy Trainer）。

平台未显式地将训练器抽象成一个类，因为在其他现有平台中都将类似训练器的实现抽象封装成一个类，导致用户难以二次开发。因此以函数的方式实现训练器，并提供了示例代码便于研究者进行定制化训练策略的开发。

2. 简单应用

接下来将通过一段伪代码的讲解来阐释上述所有抽象模块的应用。

s = env.reset()
buf = Buffer(size=10000)
agent = DQN()
for i in range(int(1e6)):
    a = agent.compute_action(s)
    s_, r, d, _ = env.step(a)
    buf.store(s, a, s_, r, d)
    s = s_
    if i % 1000 == 0:
        bs, ba, bs_, br, bd = buf.get(size=64)
        bret = calc_return(2, buf, br, bd, ...)
        agent.update(bs, ba, bs_, br, bd, bret)

以上伪代码描述了一个定制化两步回报DQN算法的训练过程。

3. 基础策略描述

区别于使用lookup table的一般强化学习，深度强化学习中学习的是神经网络黑盒$\pi$中的参数$\theta$，这里$\pi$是一个$s_{\theta }\to p(a)$的策略，因此目标函数为最大化
(1) $J={\sum }_{\tau }\pi G$。

3.1 策略梯度（PG）

上世纪九十年代被提出，依靠蒙特卡洛采样直接进行对累计折扣回报的估计，将公式 (1) 中的$\pi$改为$\log \pi$后对 $\theta$ 进行求导，然后用梯度上升法迭代求解。
$(2){\nabla }_{\theta }J={\sum }_{\tau }\pi {\nabla }_{\theta }\log \pi G=E[{\nabla }_{\theta }\log \pi G]$
形式非常简洁，计算时也很简单，展开为
(3) $E[{\Sigma }_t{\nabla }_{\theta }\log \pi (a_t|s_t)G]$
求得累计回报 G、每次采样的数据点在策略函数中的对数概率 $\log \pi (a_t|s_t)$ 之后即可对参数 $\theta$ 进行求导，从而使用梯度上升方法更新模型参数。
策略梯度算法在天授中的实现十分简单：

• process_fn：计算 G_t，具体实现位于 广义优势函数估计器（GAE）；
• forward：给定 o_t 计算动作的概率分布，并从其中进行采样返回；
• learn：按照公式 (3) 计算 G_t 与动作的对数概率 \\log\\pi_\\theta(a_t|o_t) 的乘积，求导之后进行反向传播与梯度上升，优化参数 \\theta；
• 采样策略：使用同策略的方法进行采样。

如果没有仿真模型的话，在实际过程中我们进行交互的次数往往是有限的，学习成本很高，样本不足会造成策略波动太大的问题，业界发展了一些新的方法来处理这个问题。

3.2 A2C->TRPO->PPO

A2C：优势动作评价
在Actor-Critic方法中，我们采用几种措施来降低算法的方差，首先是使用独立的模型代替轨迹的长期回报G（比如TD-error，$g_t={\Sigma }_{i=1...n}{\gamma }^i{r}_{t+i}+v(s_{t+n})-v(s_t)$），称为Critic；原来用于行动的策略模型称为Actor。
其次，在实际更新时又有异步和同步两种方法。分别称为A3C(Asynchronous Advantage Actor-Critic)和A2C(Advantage Actor-Critic)。OpenAI在官方博客中提到A2C效果比A3C要好。
再者，目标函数中加入策略的熵，以增加不确定性进行一定量的探索，并且为了让评价网络的输出尽可能接近真实的状态值函数，在优化过程中还加上了对应的均方误差项；
TRPO：置信区域策略优化
在上面的算法中，学习率α是固定的。我们想要自动选择合适的步长避免模型震荡，这里就要用到TRPO方法。TRPO全称trust region policy optimization，其目标是每次更新策略后，回报函数的值不能变差。其核心是如下公式：$J_{{\pi }^{\prime }}=J_{\pi }+E_{{\pi }^{\prime }}[{\Sigma }_t{\gamma }^t{A}_{\pi }]$
注意其中${\pi }^{\prime }$和$\pi$分别代表新策略和旧策略，后面计算期望的时候，用新策略采样，用旧策略计算优势函数。经过一系列tricky的处理之后，求解函数变为：
min ⁡ ∇ L x ∗ ( θ − x ) \\min \\nabla L_{x}*(\\theta-x)min∇L
x
​
∗(θ−x)
s.t. 1 2 ( θ − x ) T I θ ( θ − x ) ≤ δ \\frac{1}{2}(\\theta-x)^TI_{\\theta}(\\theta-x)\\le\\delta
2
1
​
(θ−x)
T
I
θ
​
(θ−x)≤δ
其中L x = E [ π x π θ A θ ] L_x=E[\\frac{\\pi_x}{\\pi_{{\\theta}}}A{\\theta}]L
x
​
=E[
π
θ
​

​

π
x
​

​
A
θ
​
]，I θ I_{\\theta}I
θ
​
为fisher阵，TRPO算法使用共轭梯度法计算fisher阵。
Baselines中的使用方法和A2C类似，把模型名字换掉即可。