MATLAB 因子分析法的案例，主要程序

Posted 2023-03-22

呵呵。这个正好我会啊。
我搞数学建模的时候做的题目很多都是数据分析，市场调查分析就是其中一种很简单的啊。
最基本的分析工具是SPSS和SAS，他们都是常用的统计工具。
你需要做哪方面的分析，就用他们的哪些功能。最常用的是回归分析。如果你不会使用这个软件，我也可以给你分析，然后把分析数据发给你啊。
你也可以去百度里面搜“问卷调查 spss”或者“市场调查 spss”，很多这样的例子，你照着做就可以分析出来了。
先发一点资料给你看：
SPSS在市场调查统计分析中的应用
SPSS是“社会科学统计软件包”（StatisticalPackagefortheSocialScience）的简称，是一种集成化的计算机数据处理应用软件，是目前世界上流行的三大统计软件之一，除了适用于社会科学之外，还适用于自然科学各领域的统计分析。将其应用于市场调查统计分析的过程，能使研究者以客观的态度，通过对受众的系统提问，收集并分析有关研究数据，以描述、解释或预测问卷调查内容的现象及其各相关因素之间的关系。在这些方面，SPSS技术的应用为市场调查实证研究中的定量分析提供了支持与保障，特别是它的易用、易学、功能强大等特点是其他方法所无法替代的。

一、SPSS的基本特点

在问卷应用于市场调查的实证研究中，会有大量的检测数据需要进行统计分析，而SPSS技术的特点恰恰适合这种实证研究的要求。其在市场调查统计的应用中具有如下特点：
1.易用、易学。SPSS采用直觉式使用界面或者说可视化界面，无需编程就可以完成工作，极大地提高了工作效率；此外，SPSS拥有强大的辅助说明系统，可帮助用户学的更快。
2.强大的表格和图形功能。SPSS能清楚地显示用户的分析结果，可以提供16种表格格式。此外，它具有顶级图形分析功能，能给出各种有用的统计图形。作为分析的一部分，它能自动生成统计结果图形，还能独立于统计过程进行图形绘制和图形分析。
3.深入分析数据的功能。除了一般常见的描述统计和推断统计外，它还包括在基本分析中最受欢迎也是在市场调查中最常用的现代统计程序，如列联表分析、主成分分析、因子分析、判别及聚类分析。

二、SPSS在市场调查统计分析的应用模式

根据上述的SPSS技术的特点和市场调查统计分析的需要，可以将SPSS在市场调查实证研究中的应用模式分为以下几种类型：

1.统计描述应用模式
统计描述应用模式指在市场调查统计分析的过程中，借助SPSS统计功能将收集到的大量数据进行分析、综合、归纳、列表、绘图等处理工作。一般而言，统计描述主要分为三方面的内容：①单变量截面数据的描述；②相对数的统计描述；③双变量截面数据的描述。SPSS最常用于描述性分析的五个过程集中在DescriptiveStatistics菜单中，分别为：Frequencies过程；Descriptives过程；Explore过程；Crosstabs过程；Ratio过程。
统计描述应用模式不仅可以使研究者了解事物的性质，而且其统计量还是对事物进行推断统计的依据。

2.假设检验应用模式
在市场调查中，通常所关心的是总体的某些特征和分布规律，而问卷调查只可以考察总体的一部分或一个样本，统计推断和假设检验就是用样本去推断总体，实质上就是凭借概率理论用观察到的部分随机变量资料来推断总体随机变量的概率分布或数字特征，如期望值和方差等，并且作出具有一定可靠程度的估计和判断。

3.量表分析应用模式
客观世界是普遍联系的统一整体，事物之间存在着相互依存、相互制约、相互影响的关系。市场活动中的许多现象也不例外，也都有其产生的原因，都要受一定因素的制约，都是一定原因的必然结果。通过不同事物“量”的变化可以观察并测量出事物之间的相互关系、密切程度、因果关系、交互效应等。在市场调查中，量表分析应用模式主要指通过对不同因子之间的发展变化而揭示出因子之间关系结果的方式。量表分析主要包括以下几种分析：回归分析、聚类分析、判别分析、因子分析、相关分析、可靠性分析等。

三、应用案例

例如：一电器公司对某地区电冰箱的销售情况进行了市场调查，其中，年份、电冰箱销售量Y（千台）、新结婚户数X1（千户）、居民户均收入X2（千户）的资料如表1所示：

首先，分别对电冰箱销售量Y（千台）、新结婚户数X1（千户）、居民户均收入X2（千户）进行描述性统计分析，具体步骤如下：
1.运行SPSS，按Analyze→DescriptiveStatistics→Descriptives顺序打开Descriptives对话框；
2.选定Y、X1、X2变量送入Variable(s)栏中；选中Savestandardizedvaluesasvariables复选项，要求计算变量的标准化值，并保存在当前数据文件中；
3.单击Options按钮，打开对话框，选中Mean、Sum、Std.deviation、Minimum、Maximum、Range复选项；
4.在主对话框中单击OK按钮，提交运行。
输出结果如表2所示。此表中，从左到右看，分别为变量名称、观测量的频数、全距、最小值、最大值、和、均数以及标准差。

其次，分别考察Y变量与X1变量、X2变量的关系，对其进行相关分析，具体步骤如下：
1.运行SPSS，读取数据文件后按Analyze→Correlate→Bivariate顺序单击菜单项，展开对话框；
2.制定分析变量，选择源变量栏中的Y、X1、X2送入Variable(s)栏；
3.分别选择Person相关，One-tailed单尾t检验，选中Flagsignificantcorrelations复选项；
4.在主对话框中单击OK按钮，提交运行。
输出结果如表3所示。表3表在行变量与列变量的交叉单元格上市这两个变量的相关计算结果。自上而下三个统计量分别为：PersonCorrelation——皮尔逊相关系数；Sig.(1-tailed)——单尾t检验结果。对于相关系数为0的假设成立的概率；N为参与相关系数计算的有效观测量数。
表3显示，电冰箱销售量Y与新结婚户数X1、居民户均收入X2有着极强的正相关，皮尔逊相关系数分别高达0.943和0.993。

最后，从表3中可以看出电冰箱销售量Y同居民新结婚户数X1、居民户均收入X2有一定关系，可用二元线性回归预测法进行预测。具体步骤如下：
1.运行SPSS，读取数据文件后按Analyze→Regression→Linear顺序单击菜单项，展开对话框；
2.在左侧的源变量栏中选择变量Y（电冰箱销售量）作为因变量进入Dependent框中，选择X1（居民新结婚户数）、X2（居民户均收入）作为自变量进入Independent(s)框中；
3.在Method选择框中选择Stepwise（逐步回归）作为分析方式；
4.提交系统执行结果。
从输出的众多表格中选取表4（回归系数分析表）。其中，Model为回归方程模型编号，UnstandardizedCoefficients为非标准化回归系数，StandardizedCoefficients为标准化回归系数，t为偏回归系数为0的假设检验的t值，Sig.为偏回归系数为0的假设检验的显著性水平值。
表4显示，常数（Constant）、居民户均收入（X2）具有统计意义，而居民新结婚户数（X1）因显著性水平值（t=0.834＞0.5）较高而不具有统计意义。从表4中可以推出模型方程：Y=-20.771+1.387X2。若预计2006年该地区居民新婚户数为30.2千户，居民户均收入62.5千元，根据模型方程不难推出2006年电冰箱销售量Y=-20.771+1.387×62.5=65.92（千台）。上述案例为较简单的线性回归操作，实际上，多元线性回归操作包含了众多的知识和内容，较为复杂，本例从中提取出一般的规律性，便于快速学习和快速操作。

四、结语

综合上述SPSS技术的应用案例，SPSS技术在市场调查统计分析中应用的一般方法：
1.录入编辑市场调查中的数据；
2.根据研究需要以及问题的性质确定出利用SPSS的相应的哪些统计功能；
3.调用SPSS的菜单功能得到相应的统计结果以及相应的图表；
4.根据统计结果和图表进行相关分析，为市场调查提供可靠的科学依据。
上述范例给出了如何利用SPSS技术来减少市场调查研究人员的统计工作量、提高研究结果准确性、可信性的一种工作方案。
总之，SPSS技术集数据录入、数据管理、统计分析、报表制作、图形绘制为一体，为市场调查的统计分析提供了有力的支持和实用的方法，是市场调查统计分析的良好工具。

：）友情提示：20份的文件调查太少了，分析出来的结果不具有代表性啊。
参考技术A 用spss点几下鼠标就出来了！而且spss也很小比较好下载

因子分析（factor analysis）案例（matlab实现）

模型介绍：
值得注意的是，特殊因子是不能被公共因子包含的。


载荷矩阵的几个统计性质：

下面通过一个例题来展示。

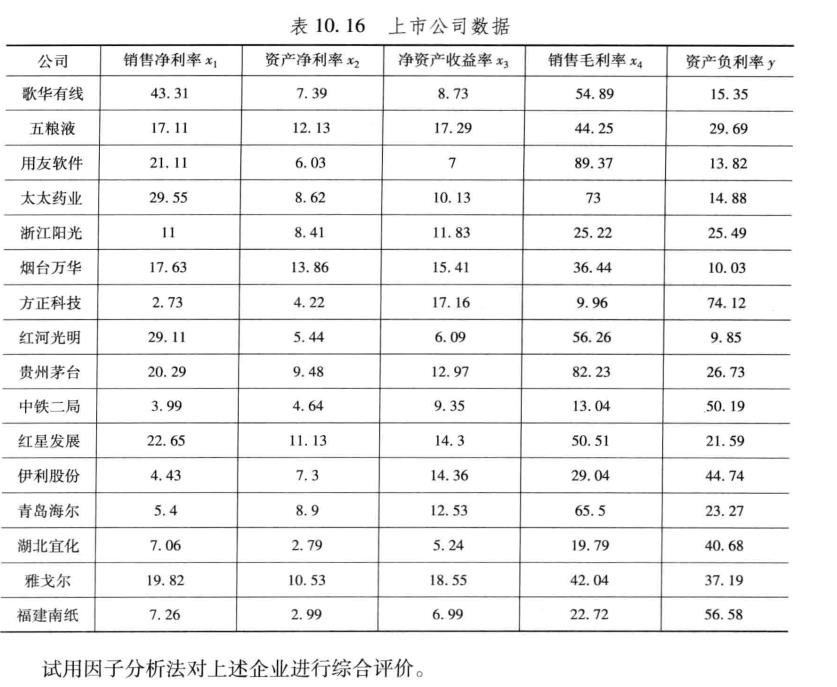
ssgs = [43.31 7.39 8.73 54.89 15.35
    17.11 12.13 17.29 44.25 29.69
    21.11 6.03 7 89.37 13.82
    29.55 8.62 10.13 73 14.88
    11 8.41 11.83 25.22 25.49
    17.63 13.86 15.41 36.44 10.03
    2.73 4.22 17.16 9.96 74.12
    29.11 5.44 6.09 56.26 9.85
    20.29 9.48 12.97 82.23 26.73
    3.99 4.64 9.35 13.04 50.19
    22.65 11.13 14.3 50.51 21.59
    4.43 7.3 14.36 29.04 44.74
    5.4 8.9 12.53 65.5 23.27
    7.06 2.79 5.24 19.79 40.68
    19.82 10.53 18.55 42.04 37.19
    7.26 2.99 6.99 22.72 56.58];
n = size(ssgs, 1);
x = ssgs(:, [1:4]);
y = ssgs(:, 5);
x = zscore(x); % 对前四个收益指标标准化处理

r = corrcoef(x);  % 计算相关系数矩阵（皮尔逊系数）

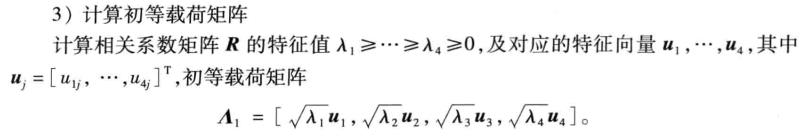
[vec1, val, con1] = pcacov(r)
f1 = repmat(sign(sum(vec1)), size(vec1, 1), 1);
vec2 = vec1.*f1; % mu
f2 = repmat(sqrt(val)', size(vec2, 1), 1); % 根号lamda
a = vec2 .* f2 % 根号lamda * mu 初等载荷矩阵

这里<=4因为总共就4个

num = input('请选择主因子个数'); % 选择主因子个数
am = a(:, [1:num]); % 提出num个主因子的载荷矩阵
[bm, t] = rotatefactors(am, 'method', 'varimax') %am旋转变换，bm为旋转后的载荷阵
bt = [bm, a(:, [num+1:end])]; % 旋转后全部因子的载荷矩阵，前两个旋转，后面不旋转
con2 = sum(bt.^2) % 计算因子贡献
check = [con1, con2'/sum(con2) * 100] % 该语句是领会旋转意义，con1是未旋转前的贡献率
rate = con2(1:num)/sum(con2) % 计算因子贡献率

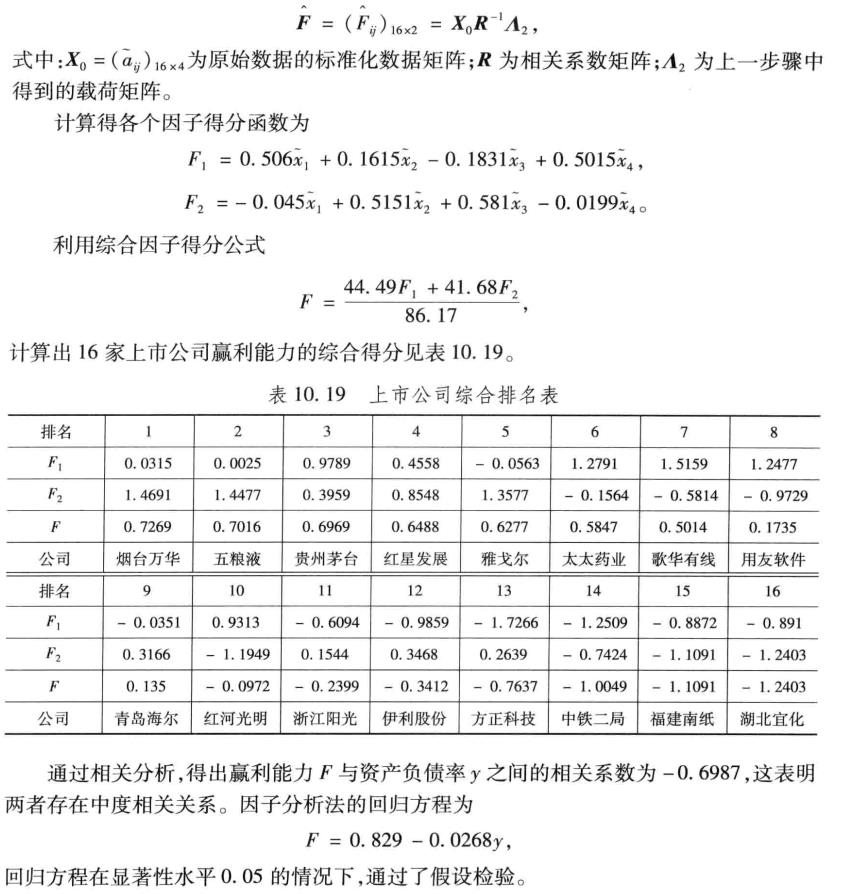
coef = inv(r) * bm % 计算得分函数的系数
score = x * coef % 计算各个因子的得分
weight = rate/sum(rate) % 计算得分的权重
Tscore = score * weight' % 对各个因子的得分进行加权求和，即求各企业的综合得分
[STscore, ind] = sort(Tscore, 'descend') % 对企业进行排序
display = [score(ind, :)'; STscore'; ind'] % 显示排序结果
[ccoef, p] = corrcoef([Tscore, y]) % 计算F与资产负债的相关性系数
[d, dt, e, et, stats] = regress(Tscore, [ones(n, 1), y]); % 计算F与资产负债的方程
d, stats % 显示回归系数，和相关统计量的值

完整代码如下：

clc,clear

ssgs = [43.31 7.39 8.73 54.89 15.35
    17.11 12.13 17.29 44.25 29.69
    21.11 6.03 7 89.37 13.82
    29.55 8.62 10.13 73 14.88
    11 8.41 11.83 25.22 25.49
    17.63 13.86 15.41 36.44 10.03
    2.73 4.22 17.16 9.96 74.12
    29.11 5.44 6.09 56.26 9.85
    20.29 9.48 12.97 82.23 26.73
    3.99 4.64 9.35 13.04 50.19
    22.65 11.13 14.3 50.51 21.59
    4.43 7.3 14.36 29.04 44.74
    5.4 8.9 12.53 65.5 23.27
    7.06 2.79 5.24 19.79 40.68
    19.82 10.53 18.55 42.04 37.19
    7.26 2.99 6.99 22.72 56.58];
n = size(ssgs, 1);
x = ssgs(:, [1:4]);
KMO(x)

y = ssgs(:, 5);
x = zscore(x);% 对前四个收益指标标准化处理
r = corrcoef(x); % 求相关系数矩阵 
[vec1, val, con1] = pcacov(r); % 进行主成分分析的相关计算
f1 = repmat(sign(sum(vec1)), size(vec1, 1), 1);
vec2 = vec1.*f1; % 特征向量正负号转换
f2 = repmat(sqrt(val)', size(vec2, 1), 1);
a = vec2 .* f2 % 求初等载荷矩阵
num = input('请选择主因子个数'); % 选择主因子个数
am = a(:, [1:num]); % 提出num个主因子的载荷矩阵
[bm, t] = rotatefactors(am, 'method', 'varimax') %am旋转变换，bm为旋转后的载荷阵
bt = [bm, a(:, [num+1:end])]; % 旋转后全部因子的载荷矩阵，前两个旋转，后面不旋转
con2 = sum(bt.^2) % 计算因子贡献
check = [con1, con2'/sum(con2) * 100] % 该语句是领会旋转意义，con1是未旋转前的贡献率
rate = con2(1:num)/sum(con2) % 计算因子贡献率
coef = inv(r) * bm % 计算得分函数的系数
score = x * coef % 计算各个因子的得分
weight = rate/sum(rate) % 计算得分的权重
Tscore = score * weight' % 对各个因子的得分进行加权求和，即求各企业的综合得分
[STscore, ind] = sort(Tscore, 'descend') % 对企业进行排序
display = [score(ind, :)'; STscore'; ind']; % 显示排序结果
[ccoef, p] = corrcoef([Tscore, y]) % 计算F与资产负债的相关性系数
[d, dt, e, et, stats] = regress(Tscore, [ones(n, 1), y]); % 计算F与资产负债的方程
d, stats % 显示回归系数，和相关统计量的值

KMO函数的代码（评价里也不知道要不要进行检验，先放着好了）

function kmo=KMO(x)
    R=corrcoef(x); % 简单相关系数
    P=partialcorr(x);  %偏相关系数
    R_1=R-eye(size(R));  %简单相关系数减去对角线上的1
    P_1=P-eye(size(P));  %偏相关系数减去对角线上的1
    KMO=sum(R_1(:).^2)/(sum(R_1(:).^2)+sum(P_1(:).^2))
end