Seeking Multiple Solutions of Combinatorial optimization Problems: A Proof of Principle Study 学习笔记

Posted 2023-02-05 好奇小圈

文章目录

• 摘要
• 零、一些基础
• • 1.梯度近似
• 一、介绍
• 二、旅行商问题
• 三、测试套件总结
• 四、基于邻域的遗传算法
• • 1.整体框架
  • 2.邻域分组策略
  • 3.进化运算
  • 4.后处理操作
• 五、实验和分析
• • 1.实验设置
  • 2.表现衡量
  • • （1）最优路径的确定
    • （2）$F_{\beta }$度量
    • （3）多样性指标DI
  • 3.模拟结果
• 六、结论
• 七、代码解析
• 相关领域

---

摘要

多最优解决方案问题广泛存在于真实世界。在一些应用里，需要定位多个最优。然而，多数研究针对的是连续的多解决方案优化，而很少有工作致力于离散多解决方案优化。为了在离散领域推广多解决方案搜索，我们为多解决方案旅行商问题设计了一个基准测试套件和两个评价指标。此外，为了解决问题，在离散空间内遗传算法和小生境算法被合并。并与现有算法进行了比较。实验结果表明，该算法在得到的解的质量和多样性方面优于对照算法。

---

零、一些基础

1.梯度近似

一、介绍

组合优化问题（COPs）是一个离散优化的课题，需要在一个限定的解决方案区域内根据一些选择标准找到一个最优解决方案。很多COPs已经被熟知为NP-hard，例如旅行商问题（TSP）。很难由确定性的算法来计算它们，特别是当解决方案空间十分大时。在过去的几十年内，很多进化算法（EAs）已经很成功被发展来解决COPs，归功于它们的非确定性搜索特性和强有力的全局优化能力。然而，多数研究聚焦于定位一个单独的最优解决方案。但是很多实际应用需要定义多于一个最优解决方案，比如导航系统和机器人路径规划。有了一个多样化的解决方案集合，决策者可以根据自身喜好选择最合适的方案，或者他们可以在一些非期待的情况下有替代选择。

为单一问题找到多个最优解的领域通常被称为多模态优化(MMO)或多解优化，在过去一些年已经有了很多研究。然而多数研究都是关于连续MMO的，而且很少有研究致力于离散MMO。为了拓展MMO到离散优化领域，有三个问题要被考虑：（1）适合处理离散MMO问题的基线（baseline）算法；（2）在离散问题空间中用来保持多个潜力解决方案的技术；（3）一个合适的基准（benchmark）测试套件。前两个主要被优化器开发人员考虑，而第三个是一个用于评价算法表现的关键因素。在本文中，我们对这三个问题进行了原则性的论证研究，简要介绍如下。

第一个问题是选择一个适当的基线算法来编码和在离散问题空间中进化解决方案。一些EAs，比如差分进化、粒子群优化等，本质上使用浮点编码，因此它们不能直接解决离散问题。其他EAs，比如遗传算法（GA）和蚁群算法，使用整数编码方案，然后在离散或组合空间中工作。因此，在本工作里，我们选择GA作为我们的基线算法。然而，GA不能直接解决离散MMO问题，这是因为它将会最终集中朝向一个最优解。汇聚导致了多样性损失。

因此，第二个食物聚焦于坚持种群多样性，这是MMO的关键。在连续MMO中，最基础保持种群多样性的方法是小生境技术，比如拥挤、物种形成和邻近策略。小生境技术在本地空间内限制了解决方案进化，避免了全局汇聚。根据这种观点考虑，我们可以合并小生境技术到一个合适的基线算法来同时获得不同的候选方案。特别的，我们发展了离散空间的邻域小生境策略，接着合并该策略到遗传算法中，以此来解决MMO问题。

第三个问题关心离散MMO问题的基准套件选择。尽管COPs的多样化解决方案优化是很多实际应用的关键，但是当前该领域只获得了很少的关注，同时缺少一个标准的测试套件来评估相关算法。缺乏适当的基准测试套件可能会阻碍离散MMO领域的研究和开发。为了推广到该领域，本文中，我们为组合MMO开发了一个基准套件。因为TSP是最火热的、最具代表性的COP，我们以它为例设计了一个多解决方案的TSP实例（MSTSPs）。据我们所知，有几种早起的MSTSP实例已经被报告。然而，这些实例要么包含太多的最佳路径(例如，16个城市，938个最佳)，要么拥有少量的城市(少于10个城市)，这是不适当的，也不足以用作基准测试套件。在本文中，我们提出了一个包含25个MSTSP实例的基准测试套件，它们可分为三类，即简单的MSTSPs、几何的MSTSPs和复合的MSTSPs。城市的数量从9到66，最优解数量的数量从2到196。

本文的其余部分组织如下。第二节制定了TSP。第三节描述了提议的25个MSTSP。该算法在第四节中提出。第五节定义了实验设置，并报告了实验结果。最后，在第六节中得出了结论。

二、旅行商问题

给定一定数量的城市和两两之间的距离信息，一个商人只访问每个城市一次，以构建一个Hamilton路径（由指定的起点前往指定的终点，途中经过所有其他节点且只经过一次）。TSP的目标是寻找一个最短的Hamilton路径。以数学形式来说，考虑一个图$G=(V,E)$，其中$V=1,2,3,...,N$是城市的集合（以索引表示），同时$E=(i,j)|i,j\in N,i\ne j$是边的集合，表示城市$i$和$j$之间的连接。每个连接$(i,j)$有一个权重值$d_{ij}$来衡量两个城市之间的距离。根据文献中定义的边权类型EUC_2D，我们将距离舍入到最近的整数。

Hamilton路径可以表示为城市集的排列$\pi$。此后，TSP是在所有的排列中找到一个最短的路径。更准确地说，我们认为，
$$\min f(\pi )=\sum _{k=1}^{N-1}{d}_{\pi (k)\pi (k+1)}+d_{\pi (N)\pi (1)}$$
其中，$N$是城市数量，$\pi (k)$是排列$\pi$的第$k$个元素。

三、测试套件总结

我们的基准测试集包括25个MSTSP。根据其设计方法，将其分为三类，一般描述如下。

第一类（MSTSP1 - MSTSP6）由6个简单的MSTSPs组成，它们的城市是随机生成的。对于这些情况，我们通过蛮力搜索（brute-force search）得到了地面真实的最佳解。然而，由于解决方案空间随着城市数量的增加而呈指数增长，对于相对大规模的实例，考虑到时间限制，不可能遍历所有可能的排列。因此，在这一类别中，城市的数量从9个到12个不等。此外，最优值的数量范围为2到13个。例如，MSTSP1如图1所示，黑色圆圈代表城市，红线构成最佳游览。特别是，MSTSP1有三个最优行程，每个都在图1的子图中描述。每个最优值的长度显示在子图的上方。可以观察到，三个最优方案具有完全相同的长度680，但行程不同。

第二类（MSTSP7 - MSTSP12）包括6个几何MSTSPs。不像第一类实例是随机生成的，现在我们利用对称几何来构造MSTSPs。通过设计不同的几何拓扑，这些实例可以有不同数量的最优值。因此，在MSTSP7 - MSTSP12中，最优城市的数量在4到196个之间，而城市的数量在10到15个之间。具体地说，使用了不同的对称几何图形，包括矩形、规则五边形和规则六边形。城市位于每个几何图形的顶点上。在不同的几何形状下，最优值对每个实例都有显著不同的行程。我们以MSTSP9为例，如图2所示。一个规则的六边形嵌套在一个大矩形中，从而产生四个最优行程。从图2中可以看出，这四种旅游项目具有完全不同的拓扑结构。

第三类（MSTSP13 - MSTSP25）由13个复合MSTSPs组成，它们是相对大规模的实例。复合MSTSPs是由一些基本的小规模MSTSPs构建的。每个小规模的MSTSP被认为是一个城市集群，城市集群分布在复合MSTSP中不同的不同几何位置。一方面，一些城市集群具有相同长度的不同子路径，从而为复合MSTSP提供了多种最优路径。另一方面，城市集群的几何分布为复合实例有多个不同的解决方案提供了额外的可能性。因此，综上所述，最优旅游的多样性同时来自于城市之间的集群内关系和城市集群之间的集群间关系。对于MSTSP13 - MSTSP25，最大城市规模提高到66，而最优的数量从4到72。更具体地说，城市集群可以被设计为几何位置（如从MSTSP13到MSTSP 16的案例）或随机生成的位置（如从MSTSP17到MSTSP25的案例）。此外，在集群间关系方面，MSTSP13和MSTSP14对城市集群具有单一的最优路径，而其他复合MSTSPs在城市集群间具有多个最优游。例如，MSTSP21有两个最优的簇间拓扑，如图3(a).的两个子图所示此外，该实例有四个城市集群，分别用A、B、C和D标记，使用一个下标和最优拓扑的索引。如果我们放大其中一个城市群(例如，B1)以查看更多细节，如图3(b)所示，该集群具有两种不同的最佳集群内拓扑。类似地，如图3 ©所示的集群B2具有两个不同的集群内拓扑，且子行程长度相同。

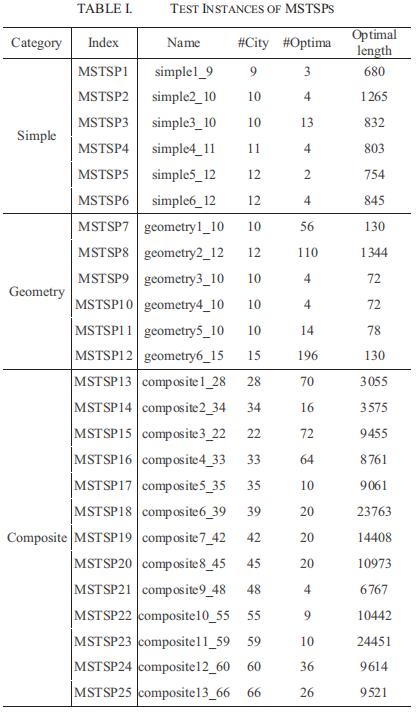
上述三个类别共包含25个MSTSPs，汇总如表一所示，包括类别信息、索引、名称、城市数量、最优数量和最优长度。有关更多细节，请参阅基准测试套件的补充文件和源代码。它们可以在互联网上下载（Github）。

四、基于邻域的遗传算法

1.整体框架

首先，NGA初始化NP染色体并计算它们的行程长度。接下来，算法进入进化循环。采用邻近策略，将整个种群划分为几个群体，最终形成一个交配池。然后，交配池中成对的亲本执行部分映射交叉(PMX)。在这之后，我们通过在两个随机选择的位置之间逆转基因组来突变染色体，称为反向序列突变(RSM)。到目前为止，我们获得了后代以及它们的行程长度。然后，我们从后代中选择染色体来确定下一代的父母。重复上述过程，直到满足终止条件。当算法终止时，采用后处理方法识别最终总体的代表性解，并输出解集。整个过程在算法1中给出。

2.邻域分组策略

邻域分组策略根据个体的距离对整个种群进行划分。如算法2所示，首先创建$tmpParent$，既$Parent$的副本。然后，将行程最短的染色体被确定为邻域领袖$Leader$。随后，与$Leader$更近的成员更倾向于形成一个小组。为此，需要在MSTSPs的解之间进行相似性度量。

注意，MSTSP的解决方案被编码为一个排列，因此直接比较相关位置的城市索引是无意义的。相反，城市之间的邻接信息更为重要。因此，我们根据两个行程之间的共同边来定义相似性度量。假定${\pi }_i$和${\pi }_j$为两个排列，而$\Phi ({\pi }_i)$和$\Phi ({\pi }_j)$贡献了他们的边集合。然后，${\pi }_i$和${\pi }_j$之间的相似度被计算为，
$$S\left({\pi }_i,{\pi }_j\right)=\frac{\left|\Phi \left({\pi }_i\right)\cap \Phi \left({\pi }_j\right)\right|}{N}$$
其中，$|\cdot |$表示交点集中的边数。然后，计算$Leadaer$和所有成员之间的相似度值。计算值用于按升序对$tmpParent$进行排序，获得$sortParent$。前$m$条$sortParent$染色体一起形成$NeighborGroup$。此外，我们还考虑了局部最优的陷阱造成的多样性损失。在$NeighborGroup$上采用了一种多样性增强的方法，以避免搜索进入局部最优。具体来说，如果$NeighborGroup$的所有成员都是相同的，我们重新初始化$m-1$成员，让一个成员保持不变。然后，社区组织被打乱了。当$NeighborGroup$的成员定居下来后，他们就会被添加到$MatingPool$。同时，新添加的成员将从$tmpParent$中删除。重复上述过程，直到集合$tmpParent$为空。

3.进化运算

遗传算法的基本进化操作包括交叉、突变和选择，如算法1的第5 - 8行所示。这三个操作都应用于同一邻域组内，以避免全局收敛。具体来说，对同一邻域群的父对采用交叉和突变操作。也就是说，后代的大部分基因片段都是来自同一邻居群体的成员，因此后代和父母往往彼此接近。选择操作保持了优越性和多样化的解决方案，而抛弃了其他的解决方案。对于每个子代，将识别出相应邻域组中最相似的父代。将比较子代和此父代之间的长度值。如果子代较短，它将取代所选择的父母。

4.后处理操作

当算法终止时，得到NP染色体，对应NP解。然而，由于冗余性或劣性，有些是不必要提供的。考虑到这一点，采用后处理方法来识别具有代表性的产品，并将其提供到最终的输出集中。该过程在算法3中描述。首先，找到长度最短的解，并将长度记录为$ShortestLength$。接着，一个选择阈值$thrLength$被定义为$ShortestLength$的一个$\epsilon$-宽松。然后我们依次处理NP解决方案：我们首先检查他们是否已经存在于最终输出集合$\mathbb{S}$。如果存在，则冗余的解决方案将会被丢弃。否则，我们允许解决方法加入集合$\mathbb{S}$，但是要符合两个条件：（1）它的长度与迄今为止的最优算法的长度完全相同（如算法3的第10 - 11行所示），并且（2）它的长度短于$以上是关于Seeking\; Multiple\; Solutions\; of\; Combinatorial\; optimization\; Problems:\; A\; Proof\; of\; Principle\; Study\; 学习笔记的主要内容，如果未能解决你的问题，请参考以下文章$

leetcode--Learn one iterative inorder traversal, apply it to multiple tree questions (Java Solution)

Solution of Publishing failed with multiple errors Error copying file static

论文阅读笔记《CAsT-19: A Dataset for Conversational Information Seeking》

论文阅读笔记《CAsT-19: A Dataset for Conversational Information Seeking》

被指针弄晕了，望帮忙拔云见日（二级指针，字符数组，字符串，强制转换（just for key words of seeking)

努力优化 Rails WHERE NOT IN 在 Rails 中的查询