无标题
Posted 莫川
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了无标题相关的知识,希望对你有一定的参考价值。
有趣的BackTracking回溯算法
最近无意中看了一些需要使用到「回溯算法」的实例,想起了读书时候的几种类型的提名,时隔多年,做个简单的回顾;
1.二叉树的遍历
public class TreeSearchDemo
public static void main(String[] args)
new TreeSearchDemo().testBinTree1();
public void testBinTree1()
TreeNode root = makeTestTree();
List<TreeNode> result = new ArrayList<>();
preOrder(root, result);
//inOrder(root, result);
//postOrder(root, result);
for (TreeNode item : result)
System.out.print(item.data);
System.out.println();
/**
* 前序遍历
*
* @param root
* @param result
*/
public void preOrder(TreeNode root, List<TreeNode> result)
if (root == null)
return;
result.add(root);
preOrder(root.left, result);
preOrder(root.right, result);
/**
* 中序遍历
*
* @param root
* @param result
*/
public void inOrder(TreeNode root, List<TreeNode> result)
if (root == null)
return;
inOrder(root.left, result);
result.add(root);
inOrder(root.right, result);
/**
* 后续遍历
*
* @param root
* @param result
*/
public void postOrder(TreeNode root, List<TreeNode> result)
if (root == null)
return;
postOrder(root.left, result);
result.add(root);
postOrder(root.right, result);
public static class TreeNode
TreeNode left;
TreeNode right;
String data;
private TreeNode makeTestTree()
TreeNode root = new TreeNode();
root.data = "A";
TreeNode nodeB = new TreeNode();
nodeB.data = "B";
TreeNode nodeC = new TreeNode();
nodeC.data = "C";
TreeNode nodeD = new TreeNode();
nodeD.data = "D";
TreeNode nodeE = new TreeNode();
nodeE.data = "E";
TreeNode nodeF = new TreeNode();
nodeF.data = "F";
//设置节点的关系
root.left = nodeB;
root.right = nodeC;
nodeB.left = nodeD;
nodeB.right = nodeE;
nodeE.right = nodeF;
return root;
构建的二叉树,图示详见:https://blog.csdn.net/nupt123456789/article/details/21193175
2.二叉树遍历的遍历「路径」
以「先序」遍历为例,我们如何记录遍历的路径呢?
- 以先序遍历为例
public void testBinTreeTracking()
//构建测试的二叉树
TreeNode root = makeTestTree();
//保存遍历的结果
List<String> result = new ArrayList<>();
//遍历时搜索的路径
LinkedList<TreeNode> tracking = new LinkedList<>();
//保存所有遍历时搜索的路径
List<LinkedList<TreeNode>> trackingResult = new ArrayList<>();
//先顺遍历先遍历根节点
tracking.add(root);
preOrderWithTracking(root, result, tracking, trackingResult);
//遍历路径
for (LinkedList<TreeNode> trackingItem : trackingResult)
for (TreeNode node : trackingItem)
if (node != null)
System.out.print("->");
System.out.print(node.data);
if (node == null)
System.out.print("->");
System.out.print(" NULL");
System.out.println();
/**
* 先序遍历的遍历路径
*
* @param root
* @param result
* @param tracking
* @param trackingResult
*/
public void preOrderWithTracking(TreeNode root, List<String> result, LinkedList<TreeNode> tracking, List<LinkedList<TreeNode>> trackingResult)
if (root == null)
trackingResult.add(new LinkedList<>(tracking));
return;
result.add(root.data);
tracking.add(root.left);
preOrderWithTracking(root.left, result, tracking, trackingResult);
tracking.removeLast();
tracking.add(root.right);
preOrderWithTracking(root.right, result, tracking, trackingResult);
tracking.removeLast();
- 输出结果
->A->B->D-> NULL
->A->B->D-> NULL
->A->B->E-> NULL
->A->B->E->F-> NULL
->A->B->E->F-> NULL
->A->C-> NULL
->A->C-> NULL
可以看出,之前我们遍历二叉树,以root==null作为判断条件时,所有的搜索路径,这里面对于叶子节点,会有2条重复的搜索结果,主要是由于分别遍历其左右子树,均为null,所有会出现2次搜索结果;
3.二叉树的最大深度
由上面二叉树的遍历,我们把遍历终止时的每一个遍历路径都打印了一遍,因此可以根据路径的size判断出二叉树的深度;
4.多叉树的搜索
- 文件目录的搜索
/**
* 递归遍历文件下的所有文件=>查找多叉树的叶子节点
*
* @param dir
* @param allFile
*/
public void listAllFile(File dir, List<File> allFile)
if (dir.isFile())
allFile.add(dir);
return;
File[] children = dir.listFiles();
for (int i = 0; i < children.length; i++)
listAllFile(children[i], allFile);
- 文件搜索时,搜索到叶子节点的所有路径
public void listAllFilesWithTracking(File dir, LinkedList<File> tracking, List<LinkedList<File>> allTracking)
if (dir.isFile())
//遍历到[文件],也就是叶子节点,返回,记录tracking路径
allTracking.add(new LinkedList<>(tracking));
return;
File[] children = dir.listFiles();
for (int i = 0; i < children.length; i++)
tracking.add(children[i]);
listAllFilesWithTracking(children[i], tracking, allTracking);
tracking.removeLast();
5.回溯算法的模板
public void backtracking(选择列表,路径LinkedList tracking,所有路径resultTracking)
if(结束条件)
resultTracking.add(new LinkedList<>(tracking));//保存路径
return;
for (选择 in 选择列表)
tracking.add(选择)//做选择,将选择加入到选择列表
backtracking(选择列表,路径LinkedList tracking,所有路径List<LinkedList> resultTracking)
tracking.removeLast()//删除最后一个,撤销选择
从回溯算法的模板,再回看二叉树的遍历,其实相当于选择列表是二叉树的两个根节点[root.left,root.right],而且选择列表的具体引用是「变化」的;而回溯算法的「选择列表」一般是比较稳定的
6.暴力破解密码问题
小明无意中听到同坐的密码是有[1,2,3,4]4个数字组成,而且密码有6位数字,小明如何枚举所有的密码组成?有排列组合知识我们知道,总共有4的6次方种,那代码实现具体是什么呢?
package com.mochuan.test.bt;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/**
* 所有密码的组合
*/
public class AllPassword
private int depth = 6;
public static void main(String[] args)
new AllPassword().test();
public void test()
int[] word = 1, 2, 3, 4;
LinkedList<Integer> tracking = new LinkedList<>();
List<LinkedList<Integer>> allResult = new ArrayList<>();
backtracking(word, tracking, allResult);
System.out.println("结果总数:" + allResult.size());
for (LinkedList trackingItem : allResult)
System.out.println(trackingItem);
public void backtracking(int[] word, LinkedList<Integer> tracking, List<LinkedList<Integer>> allResult)
//搜索的深度:即密码的长度
if (tracking.size() >= depth)
allResult.add(new LinkedList<>(tracking));
return;
for (int i = 0; i < word.length; i++)
tracking.add(word[i]);//做选择
backtracking(word, tracking, allResult);
tracking.removeLast();//回溯:撤销选择
从代码运行可见,时间复杂度很高O(N^K),N的K次方;后续的很多的问题,都是以这个为模板,对深度为K的完全N叉树进行搜索;以word=1,2,depth = 3为例,有2^3=8种结果,如下:
结果总数:8
[1, 1, 1]
[1, 1, 2]
[1, 2, 1]
[1, 2, 2]
[2, 1, 1]
[2, 1, 2]
[2, 2, 1]
[2, 2, 2]
如果以word=1,2,3,depth = 3为例,有3^3=27种结果,它的搜索空间为:
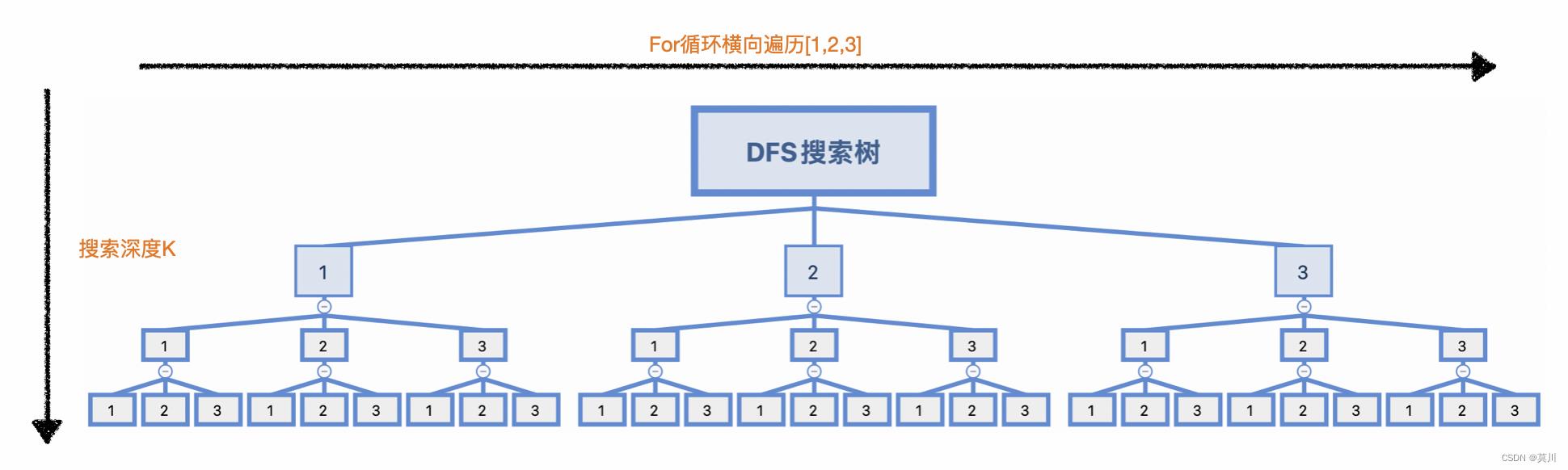
7.全排列问题
全排列问题,与上述的密码组合问题相比,做了部分的「剪枝」,将搜索的复杂度降低到O(n!),每次的tracking结果,无重复的元素,做一下去重;因此,全排列问题如下:
- 搜索终止条件
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class PermutationsDemo
public static void main(String[] args)
new PermutationsDemo().test();
public void test()
int[] word = 1, 2, 3;
LinkedList<Integer> tracking = new LinkedList<>();
List<LinkedList<Integer>> allResult = new ArrayList<>();
backtracking(word, tracking, allResult);
System.out.println("结果总数:" + allResult.size());
for (LinkedList trackingItem : allResult)
System.out.println(trackingItem);
public void backtracking(int[] word, LinkedList<Integer> tracking, List<LinkedList<Integer>> allResult)
//搜索的深度:即密码的长度
if (tracking.size() == word.length)
allResult.add(new LinkedList<>(tracking));
return;
for (int i = 0; i < word.length; i++)
if (tracking.contains(word[i]))
//去除重复元素
continue;
tracking.add(word[i]);//做选择
backtracking(word, tracking, allResult);
tracking.removeLast();//回溯:撤销选择
demo的全排列结果
结果总数:6
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]
8.子集问题
一个集合[1,2,3],它有多少个子集?这个也是用到回溯,遍历集合里的所有元素,但
- 迭代去重1:集合里的元素是不重复的,需要做去重
- 搜集元素:集合里的元素,没有顺序,需要对不同顺序的进行去重;
- 终止条件不变
- 搜集元素的位置和终止条件不同,这块需要注意;
package com.mochuan.test.bt;
import java.util.*;
public class AllSubSet
public static void main(String[] args)
new AllSubSet().test();
public void test()
int[] word = 1, 2, 3;
LinkedList<Integer> tracking = new LinkedList<>();
HashMap<String, LinkedList<Integer>> memo = new HashMap<>();
backtracking(word, tracking, memo);
System.out.println("结果总数:" + memo.size());
for (Map.Entry<String, LinkedList<Integer>> trackingItem : memo.entrySet())
System.out.println(trackingItem.getValue());
public String genKey(LinkedList<Integer> tracking)
if (以上是关于无标题的主要内容,如果未能解决你的问题,请参考以下文章