2022-11-07:给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。 图用一个大小为 n 下标从 0 开始的数组 edges 表示, 节点 i 到
Posted 福大大架构师每日一题
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022-11-07:给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。 图用一个大小为 n 下标从 0 开始的数组 edges 表示, 节点 i 到相关的知识,希望对你有一定的参考价值。
2022-11-07:给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,
节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
输入:edges = [3,3,4,2,3]。
输出:3。
答案2022-11-07:
一个环指的是起点和终点是 同一个 节点的路径。
用强联通分量。
代码用rust编写。代码如下:
use std::iter::repeat;
impl Solution
pub fn longest_cycle(edges: Vec<i32>) -> i32
let n = edges.len() as i32;
let mut graph: Vec<Vec<i32>> = repeat(vec![]).take(n as usize).collect();
for i in 0..n
if edges[i as usize] != -1
graph[i as usize].push(edges[i as usize]);
let mut connected_components = StronglyConnectedComponents::new(graph);
let m = connected_components.get_sccn() + 1;
let mut cnt: Vec<i32> = repeat(0).take(m as usize).collect();
let scc = connected_components.get_scc();
for i in 0..n
cnt[scc[i as usize] as usize] += 1;
let mut ans = -1;
for count in cnt.iter()
ans = get_max(ans, if *count > 1 *count else -1 );
return ans;
struct StronglyConnectedComponents
nexts: Vec<Vec<i32>>,
n: i32,
stack_size: i32,
cnt: i32,
sccn: i32,
stack: Vec<i32>,
dfn: Vec<i32>,
low: Vec<i32>,
scc: Vec<i32>,
impl StronglyConnectedComponents
pub fn new(edges: Vec<Vec<i32>>) -> Self
let mut ans: StronglyConnectedComponents = StronglyConnectedComponents
nexts: edges,
n: 0,
stack_size: 0,
cnt: 0,
sccn: 0,
stack: vec![],
dfn: vec![],
low: vec![],
scc: vec![],
;
ans.init();
ans.scc();
return ans;
fn init(&mut self)
self.n = self.nexts.len() as i32;
self.stack_size = 0;
self.cnt = 0;
self.sccn = 0;
self.stack = repeat(0).take(self.n as usize).collect();
self.dfn = repeat(0).take(self.n as usize).collect();
self.low = repeat(0).take(self.n as usize).collect();
self.scc = repeat(0).take(self.n as usize).collect();
fn scc(&mut self)
for i in 0..self.n
if self.dfn[i as usize] == 0
self.tarjan(i);
fn tarjan(&mut self, p: i32)
self.cnt += 1;
self.dfn[p as usize] = self.cnt;
self.low[p as usize] = self.dfn[p as usize];
self.stack[self.stack_size as usize] = p;
self.stack_size += 1;
for q in self.nexts[p as usize].clone().iter()
if self.dfn[*q as usize] == 0
self.tarjan(*q);
if self.scc[*q as usize] == 0
self.low[p as usize] = get_min(self.low[p as usize], self.low[*q as usize]);
if self.low[p as usize] == self.dfn[p as usize]
self.sccn += 1;
let mut top = 0;
self.stack_size -= 1;
top = self.stack[self.stack_size as usize];
self.scc[top as usize] = self.sccn;
while top != p
self.stack_size -= 1;
top = self.stack[self.stack_size as usize];
self.scc[top as usize] = self.sccn;
fn get_scc(&mut self) -> &Vec<i32>
return &self.scc;
fn get_sccn(&mut self) -> i32
return self.sccn;
fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T
if a < b
a
else
b
fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T
if a > b
a
else
b
fn main()
let edges = vec![3, 3, 4, 2, 3];
let ans = Solution::longest_cycle(edges);
println!("ans = ", ans);
let edges = vec![2, -1, 3, 1];
let ans = Solution::longest_cycle(edges);
println!("ans = ", ans);
struct Solution
执行结果如下:
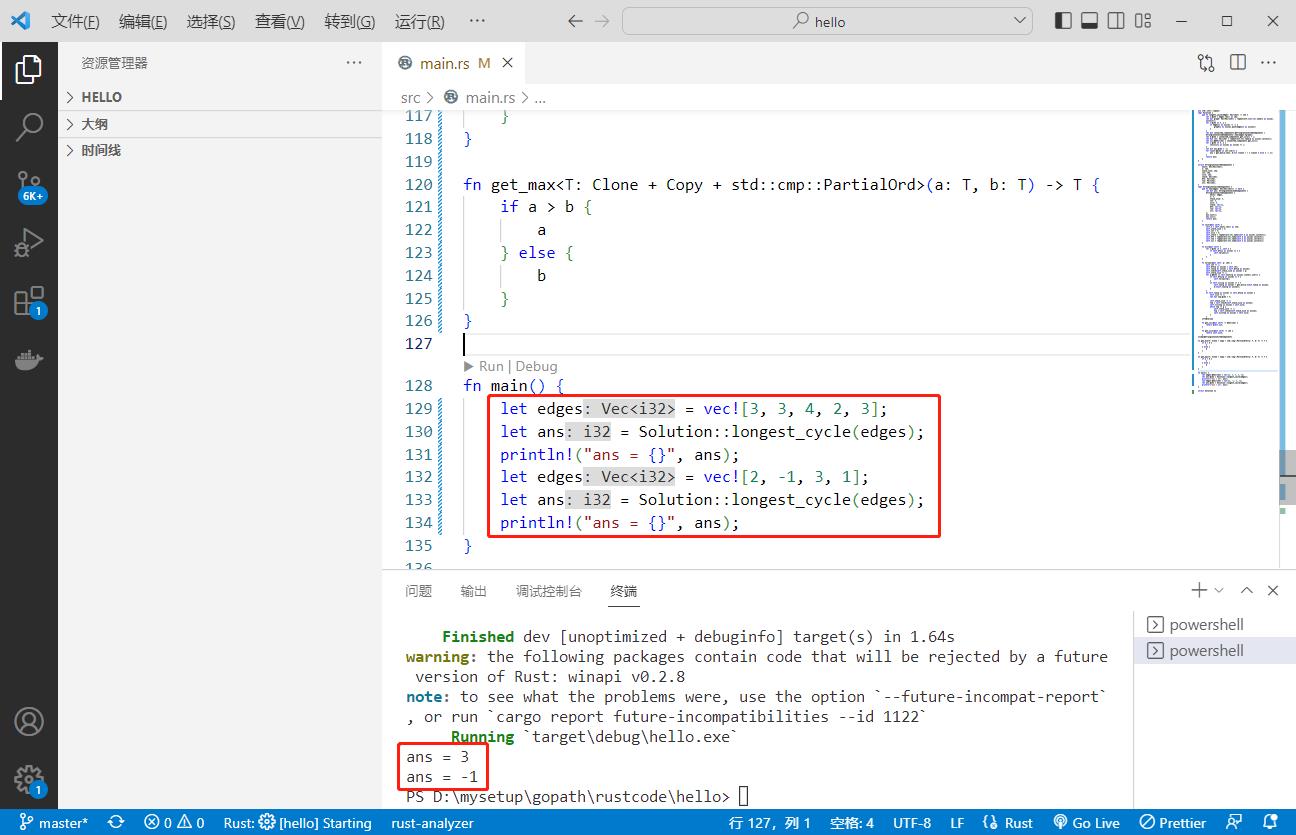
以上是关于2022-11-07:给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。 图用一个大小为 n 下标从 0 开始的数组 edges 表示, 节点 i 到的主要内容,如果未能解决你的问题,请参考以下文章