LeetCode每周算法零钱兑换
Posted Java仗剑走天涯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode每周算法零钱兑换相关的知识,希望对你有一定的参考价值。
题目来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/coin-change
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
示例 4:
输入:coins = [1], amount = 1
输出:1
示例 5:
输入:coins = [1], amount = 2
输出:2
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104
分析
一些分析内容,借鉴自博客:https://juejin.cn/post/6985150114134229022
怎么感觉像是回到了小学应用题?
1、暴力穷举逐个排除
简单分析一下: 最小硬币组合 -> 尽量用大的硬币
这傻不拉几的题谁出的,这么简单
7+7+7=21,21+2+2+2=27, 6枚硬币
卧槽
7+5+5+5+5=27, 5枚硬币
我们可以很暴力的想一想,从大往小的算,可以加起来不超过27,比如
7+7+7+7 > 27 (排除)
7+7+7+5 或者 7 +7 +7+2+2+2 6枚
....
穷举太慢了,还会涉及到很多的重复计算,如果我想要27以内的任何值最小的硬币组合呢,想想都头大了吧。
既然计算机可以通过内存保存之前的内容,又快,很明显,我们开一个数组来保存之前的状态。
2.动态规划分析
虽然我们不知道最优策略是什么,但是最优策略肯定是K枚硬币,a1, a2, ....ak面值加起来是27
所以一定有一枚最后的硬币:ak. 除掉这么硬币,前面硬币的面值加起来是27-ak
关键点1:
- 我们不关心前面的k-1枚硬币是怎么拼出27-ak的(可能有一种拼法,也可能有100种拼法),而且我们现在甚至还不知道ak和K, 但是我们确定前面的硬币拼出了27-ak
关键点2:
- 因为是最优策略, 所以拼出27-ak的硬币数一定要最少,否则这就不是最优策略了
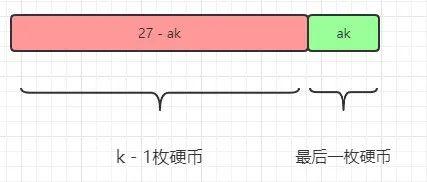
子问题
- 所以我们就要求:最少用多少枚硬币可以拼出27-ak
- 原问题是最少用多少枚硬币拼出27
- 我们将原问题转化了一个子问题,而且规模更小:27-ak
- 为了简化定义, 我们设状态f(x)=最少用多少枚硬币拼出x
等等,我们还不知道最后的那枚硬币ak是多少
- 很明显,最后的那枚硬币只能是2,5或者7
- 如果ak是2, f(27)应该是f(27-2)+1(1代表最后一枚硬币2)
- 如果ak是5, f(27)应该是f(27-5)+1(1代表最后一枚硬币5)
- 如果ak是7, f(27)应该是f(27-7)+1(1代表最后一枚硬币7)
所以使用最少的硬币数=f(27) = minf(27-2)+1, f(27-5)+1, f(27-7)+1
2.1递归解法
private static Map<Integer, Integer> cache = new HashMap<>();
static
// 退出条件
cache.put(2, 1);
cache.put(3, -1);
cache.put(4, 2);
cache.put(5, 1);
cache.put(6, 3);
cache.put(7, 1);
// 2,5,7三种硬币
public static int minCoin(int target)
if (target < 2)
return -1;
Integer integer = cache.get(target);
if (integer != null)
return integer;
// if (target == 2)
// return 1;
//
// if (target == 3)
// return -1;
//
// if (target == 4)
// return 2;
//
// if (target == 5)
// return 1;
//
// if (target == 6)
// return 3;
//
// if (target == 7)
// return 1;
//
int[] result = minCoin(target - 2) + 1,
minCoin(target - 5) + 1,
minCoin(target - 7) + 1;
int min = min(result);
cache.put(target, min);
return min;
public static int min(int[] valArr)
if (valArr == null || valArr.length < 1)
return Integer.MIN_VALUE;
int val = Integer.MIN_VALUE;
for (int i : valArr)
if (i > 0)
val = val > 0 ? Math.min(val, i) : i;
return val;
2.2动态规划
转移方程:
- 设状态f(x)=最少用多少枚硬币拼出x
- 对于任意的x : f(X) = minf(X-2)+1, f(X-5)+1, f(X-7)+1
初始条件和边界情况:
- 提出问题
- x-2, x-5, x-7 小于0怎么办?
- 什么时候停下来?
如果不能拼出Y, 就定义f[Y] = 正无穷
例如f[-1], f[-2] = 正无穷
例如:拼不出f[1]=minf(-1)+1, f(-3)+1, f(-6)+1
初始条件:f[0] = 0
计算顺序
计算:f[1], f[2], ... f[27]
当我们计算到f[x], f[x-2], f[x-5], f[x-7] 都已经得到结果了。如图:

上图7只需要一个硬币。
f[x] = 最少用多少枚硬币拼出x
f[x] = ∞ 表示无法用硬币拼出x
public static int coinChange(int [] A, int M )
int[] f = new int[M+1];
int n = A.length;
f[0] = 0;
int i,j;
for (i = 1; i<=M; i++)
f[i] = Integer.MAX_VALUE;
for (j = 0; j< n;j++)
// 边界条件判断
if (i >= A[j] && f[i - A[j]] != Integer.MAX_VALUE)
f[i] = Math.min(f[i - A[j]] + 1, f[i]);
// System.out.println(i + "=" +f[i]);
if (f[M] == Integer.MAX_VALUE)
f[M] = -1 ;
return f[M];
以上是关于LeetCode每周算法零钱兑换的主要内容,如果未能解决你的问题,请参考以下文章