基于希尔伯特变换的光反馈自混合干涉位移实时跟踪测量系统的瞬时相位计算matlab仿真
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于希尔伯特变换的光反馈自混合干涉位移实时跟踪测量系统的瞬时相位计算matlab仿真相关的知识,希望对你有一定的参考价值。
目录
一、理论基础
光学干涉测量技术是以光波干涉原理为基础进行测量的技术,其区别于其它光学成像测量技术的特点除了具有更高的测量灵敏度和精确度,还具有非接触测量的特点,不会给测量物造成表面损伤,因此,光干涉测量技术的应用非常广泛。而希尔伯特变换和瞬时相位理论是一种较为常用方法。

因此,信号的希尔伯特变换可以看成信号通过一个单位冲激响应为的滤波器后的输出。信号经过希尔伯特变换后,其幅度频谱、功率谱及自相关函数均不变,信号的希尔伯特变换相当于一个移相器,信号的正频率部分相位变化-90°,负频率部分相位变化90°。
由连续时间信号S(t)和它的希尔伯特变换H(S(t))可以构造解析信号z(t) : 
由上述解析信号的表达式z(t) 可以得出s(t) 的瞬时相位也即是 的瞬时相位为: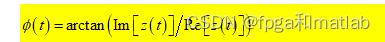
因此通过对OFSMI信号做希尔伯特变换可以构造解析信号,通过解析信号求反正切运算就可以得到OFSMI信号的瞬时相位。
希尔伯特变换整数条纹检测算法的主要内容为:对OFSMI信号 消除直流分量后做希尔伯特变换构造解析信号,由解析信号求反正切运算得包裹的瞬时相位,由包裹的瞬时相位检测所有相位突变点,并确定外部反射体的位移方向,最后去掉伪条纹点,得到所有的整数条纹点。希尔伯特变换整数条纹检测算法流程如图所示:
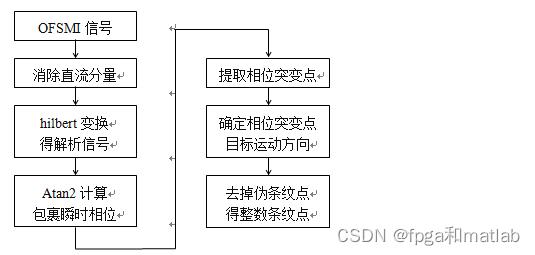
二、案例背景
光学干涉测量技术是以光波干涉原理为基础进行测量的技术,其区别于其它光学成像测量技术的特点除了具有更高的测量灵敏度和精确度,还具有非接触测量的特点,不会给测量物造成表面损伤,因此,光干涉测量技术的应用非常广泛。
在传统光干涉测量的研究过程中,人们发现激光器的外部光反馈会引起光反馈自混合干涉(optical feedback self-mixing interference,简称OFSMI)效应,影响激光器的输出特性,引起的谱线展宽、光噪声、相干碎灭等现象会给激光系统带来严重的破坏,因此起初人们总是试图消除由激光器的外部光反馈造成的影响。随着研究的进一步深入,人们发现OFSMI信号中包含有激光器的自身参数信息和外部反射物运动的一些信息,例如:位移、速度、加速度等,于是,人们从消除光反馈带来的影响转变为利用光反馈获取有关信息, OFSMI的研究才逐渐兴起,其主要应用有谱线压窄、OFSMI测量等领域。
OFSMI效应是指激光器输出光经外部反射体反射或散射后,其中一部分光又反馈回激光器谐振腔,反馈光与腔内光相干涉,从而调制激光器输出光功率的现象。
三、MATLAB程序
%设置相关参数
close all;clc;clear all
%phi_0=am0+am*sin(2*pi*ft/fs*t1);
am=19; %am=4*pi*L/lanbuda0
am0=30; % am0=4*pi*L0/lanbuda0
ft=200; %设置振动频率
fs=40000; %设置采样频率
n=400; %设置采样点数
alfa=5; %设置激光器线宽展宽因数
c=0.7; %设置光反馈强度
[x,g,y]=spain_ofsmi_data(alfa,c,am,am0,ft,fs,n);%%x----fai0, g---自混合信号, y---- fai-f
save ofsmi g; %将g保存到ofsmi.mat文件中
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%画图
figure(1)
subplot(3,1,1);plot(x);title('无光反馈时的外腔相位');ylabel('fai_0(n)/rad');grid on;%axis([-inf inf 290 340]);
subplot(3,1,2);plot(y);title('有光反馈时的外腔相位alfa=3;c=4;');ylabel('fai_f(n)/rad');grid on;
subplot(3,1,3);plot(g);title('SMI信号');xlabel('采样点数n');ylabel('g(n)的振幅');grid on;%legend();
F2 = hilbert(g);
xr = real(F2);
xi = imag(F2);
Faif_ = atan2(xi,xr);%公式8
%根据峰值flag的间隔确定flags变量,用来判断m1,m2的取值
flags = [ones(50,1);-1*ones(100,1);ones(100,1);-1*ones(100,1);ones(50,1)];
flags = [0;flags(1:end-1)];
flag2 = zeros(size(Faif_));
for i = 2:length(Faif_)-1
if i <= 51;
if g(i)<g(i-1) & g(i)<g(i+1)
flag2(i)=1;
end
end
if i <= 151 & i>51
if g(i)<g(i-1) & g(i)<g(i+1)
flag2(i)=1;
end
end
if i <= 251 & i>151
if g(i)<g(i-1) & g(i)<g(i+1)
flag2(i)=1;
end
end
if i <= 351 & i>251
if g(i)<g(i-1) & g(i)<g(i+1)
flag2(i)=1;
end
end
if i <= 400 & i>351
if g(i)<g(i-1) & g(i)<g(i+1)
flag2(i)=1;
end
end
end
flag2([51,151,251,351])=0;
flag = zeros(size(Faif_));
for n = 2:length(Faif_)
flag(n) = abs([Faif_(n-1)-Faif_(n)]);
end
[pks,locs] = findpeaks(flag,'THRESHOLD',0.5);
locs = locs;
flag3 = zeros(size(Faif_));
flag3(locs) = 1;
indx1 = find(flag2==1);
indx2 = find(flag3==1);
indxs = [];
for i = 1:length(indx1)
if abs(indx1(i)-indx2(i))<=4
indxs(i) = indx2(i);
else
indxs(i) = indx1(i);
end
end
Flag_=zeros(size(flag2));
Flag_(indxs)=1;
figure;
subplot(211);
plot(g);
subplot(212);
plot(flag2,'r');
hold on
plot(flag3,'b');
%依据相位展开原理, 计算真实相位Faif
m1 = 0;
m2 = 1;
Faif(1) = (-1)^m1*abs(Faif_(1)) + 2*pi*m2;
for n = 2:length(flag3)
%判决m1和m2,0/1,1/-1,进行分段处理
if flags(n) == 1
m2 = m2+1*Flag_(n);
if sign(Faif_(n))==1
m1=0;
else
m1=1;
end
end
if flags(n) == -1
m2 = m2-1*Flag_(n);
if sign(Faif_(n))==1
m1=1;
else
m1=0;
end
end
Faif(n) = (-1)^m1*abs(Faif_(n)) + 2*pi*m2;
end
%步骤三:
fai0 = Faif + c*sin(Faif + atan(alfa));
figure;
subplot(311);
plot(g);
ylabel('g(n)的振幅');
subplot(312);
plot(Faif_);
ylabel('Fai_f`');
subplot(313);
plot(fai0);
ylabel('Fai_0');
%计算误差
t1=fai0-mean(fai0);
t2=x-mean(x);
figure;
subplot(211);
plot(t2,'r','linewidth',2);
hold on
plot(t1,'b--','linewidth',2);
legend('真实相位','重构相位');
subplot(212);
plot(t1-t2)
title('error');
axis([0,400,-30,30]);
%%
clear;
close all;
%% 生成自混合信号
am=33;am0=50;ft=200;fs=600000;n=6000 ; alfa=4;c=0.5;
[x,g,y]=spain_ofsmi_data(alfa,c,am,am0,ft,fs,n);
t1=1:n;
t=t1
%t=t1/fs;
p0=3000;m=0.001;
p=p0*(1+m*g);
figure
plot(t1,p,'k');title('自混合信号');xlabel('采样点数');
%% 加高斯白噪声
% sur_add=25;%信噪比
% ps=g*g'/n;
sur_add=30;%信噪比
ps=9*g*g'/n;
pn=ps*10^(-sur_add/10);
noise=randn(1,n);
noise=sqrt(pn)*noise;
p=p+noise;
p1=p;
% figure
% plot(t1,noise);
figure
plot(t1,p,'k');title('自混合信号');xlabel('采样点数');
figure
subplot(2,1,1);plot(t,p,'k');ylabel('P/uw','fontsize',12);gtext('(a)','fontsize',12);
%% 均值滤波
y1=zeros(1,n)
for i=1:12
y1(i)=p(i);
end
for i=13:n-12
y1(i)=(p(i-12)+p(i-11)+p(i-10)+p(i-9)+p(i-8)+p(i-7)+p(i-6)+p(i-5)+p(i-4)+p(i-3)+p(i-2)+p(i-1)+p(i)+p(i+1)+p(i+2)+p(i+3)+p(i+4)+p(i+5)+p(i+6)+p(i+7)+p(i+8)+p(i+9)+p(i+10)+p(i+11)+p(i+12))/25;
end
for i=n-11:n
y1(i)=p(i);
end
p=y1;
% figure
% plot(t1,p,'k');title('自混合信号');xlabel('采样点数'); axis([-inf inf 2995 3003]);
%% 消去直流分量
dif=diff(p);
dif=[0 dif ];
yuzhi=max(dif)*0.6;
for i=1:length(dif);
if abs(dif(i))<yuzhi
dif_th(i)=0;
else
dif_th(i)=dif(i);
end
end
I=find(dif_th);
num=length(I);
z=[1 I n];
setsum=zeros(length(z)-1);
for i=1:length(z)-1
for j=z(i):z(i+1)
if j<z(i+1)
setsum(i)=setsum(i)+p(j);%分段求和
elseif j==z(i+1)
if i==1
for jj=z(i):z(i+1)
ave(jj)=setsum(i)/(z(i+1)-z(i));
end
else
for jj=z(i)+1:z(i+1)
ave(jj)=setsum(i)/(z(i+1)-z(i));
end
end
end
end
end
ave_g=p-ave;
% figure
% subplot(2,1,1);stem(dif);title('SM信号的微分');
% subplot(2,1,2);stem(dif_th);
% figure
% subplot(2,1,1);plot(t,p,'k');ylabel('P/uw','fontsize',13);xlabel('t/s','fontsize',13);title('(a)','fontsize',13')
% subplot(2,1,2);plot(t,ave_g,'k');xlabel('t/s','fontsize',13);ylabel('Po/uw','fontsize',13);title('(b)','fontsize',13)
%% 通过hilbert构造解析形式,检测条纹
F2=hilbert(ave_g);
xr=real(F2);xi=imag(F2);atan=atan2(xi,xr);
freq_ins=diff(atan);
freq_ins=[0 freq_ins ];
for i=1:length(freq_ins);
if freq_ins(i)>=-3
freq_ins_th(i)=0;
else
freq_ins_th(i)=sign(freq_ins(i));
end
end
II=find(freq_ins_th);
no=length(II);
jiange=(II(6)-II(1))/4/3;
for i=2:no
if II(i)<=II(i-1)+jiange;
freq_ins_th(II(i))=0;
end
end
% figure
% subplot(3,1,1);plot(t,atan,'k');title('(a)','fontsize',13');;xlabel('t/s','fontsize',13);ylabel('相位/rad','fontsize',13);
% subplot(3,1,2);plot(t,freq_ins,'k');title('(b)','fontsize',13');;xlabel('t/s','fontsize',13);ylabel('相位微分/rad','fontsize',13);
% subplot(3,1,3);plot(t,freq_ins_th,'k');title('(c)','fontsize',13');;xlabel('t/s','fontsize',13);
%% 确定运动方向
pulsed=-sign(dif);
trans=pulsed.*freq_ins_th;
%% 去掉小数条纹
xiaoshu=zeros(1,n)
for i=1:num-1
if sign(dif_th(I(i+1)))~=sign(dif_th(I(i)))
mm2=round((I(i+1)-I(i))/3);
mm1=round((I(i+1)-I(i))/4);
mm3=round((I(i+1)-I(i))/24*7);
for j=I(i)+mm1:I(i+1)-mm2
xiaoshu(j)=1;
end
else
xiaoshu(j)=0;
end
end
% figure
% plot(xiaoshu)
xiaoshu_y=xiaoshu.*p;
% figure
% plot(xiaoshu_y);title('粗糙提取小数条纹');axis([0 6000 2900 3050])
for i=1:n
if xiaoshu(i)==1
xiaoshu1(i)=0;
else
xiaoshu1(i)=1;
end
end
trans_x=trans.*xiaoshu1;
%%
% figure
% subplot(3,1,1);plot(t,p,'k');ylabel('P/uw','fontsize',13);xlabel('t/s','fontsize',13);title('(a)','fontsize',13');
% subplot(3,1,2);plot(t,trans,'k');xlabel('t/s','fontsize',13);title('(b)','fontsize',13');
% subplot(3,1,3);plot(t,trans_x,'k');xlabel('t/s','fontsize',13);title('(c)','fontsize',13');
%%
subplot(2,1,2);plot(t,trans_x,'k');xlabel('采样点n','fontsize',12);gtext('(b)','fontsize',12);四、仿真结论分析
仿真结构如下:
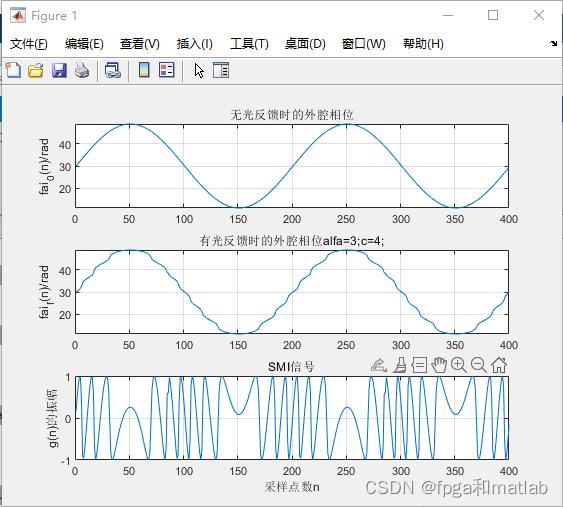
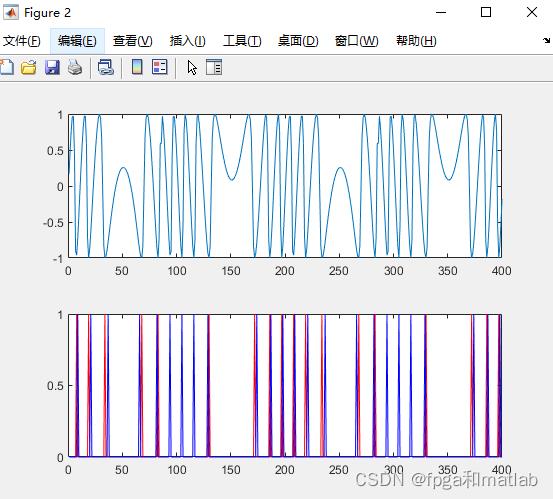



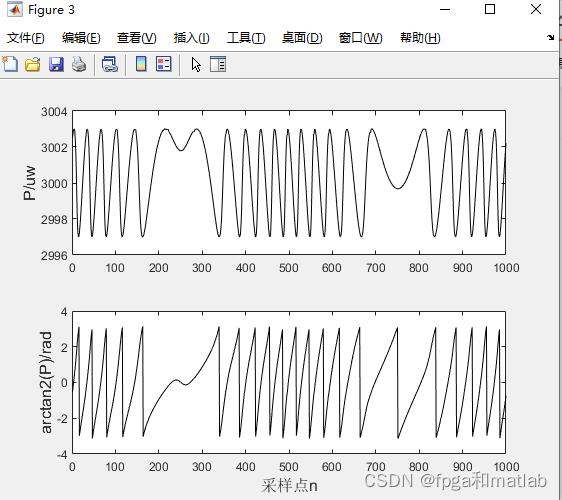
A23-45
以上是关于基于希尔伯特变换的光反馈自混合干涉位移实时跟踪测量系统的瞬时相位计算matlab仿真的主要内容,如果未能解决你的问题,请参考以下文章